ゼロから作るDeep Learning Pythonで学ぶディープラーニングの理論と実装
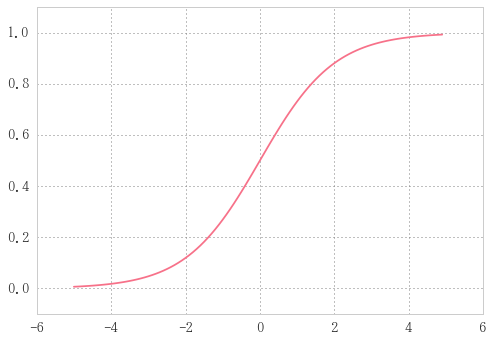
sigmoid function
from sigmoid import *
def sigmoid(x):
return 1 / (1 + np.exp(-x))
sigmoid(7)
0.9990889488055994
x = np.array([4,6,-2,-1, 2])
sigmoid(x)
array([ 0.98201379, 0.99752738, 0.11920292, 0.26894142, 0.88079708])
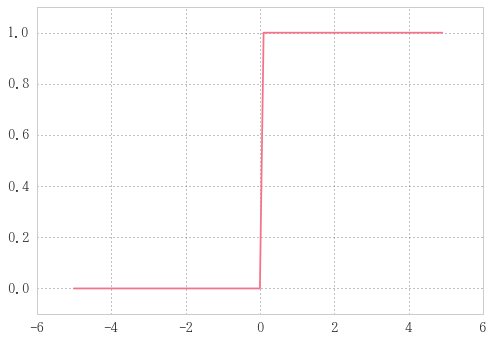
step function
from step_function import *
def step_function(x):
return np.array(x > 0, dtype=np.int)
step_function(5)
array(1)
step_function(-5)
array(0)
x = np.array([3,-6,4,-1])
step_function(x)
array([1, 0, 1, 0])
x = np.random.randn(2,3)
print(x)
print(step_function(x))
[[ 0.21780529 -0.05316613 1.28802155]
[-0.55119659 -1.23515555 0.6576237 ]]
[[1 0 1]
[0 0 1]]
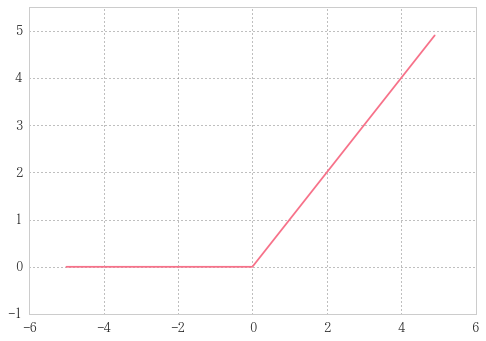
ReLU function
Rectified Linear Unit
入力が0を超えていれば、その 入力をそのまま出力し、0 以下ならば 0 を 出力する関数です
from relu import *
def relu(x):
return np.maximum(0, x)
多次元配列
B = np.array([[1,2], [3,4], [5,6]]); B
array([[1, 2],
[3, 4],
[5, 6]])
np.ndim(B)
2
B.shape
(3, 2)
A = np.array([[3,2,1], [6,5,4]])
A.dot(B)
array([[14, 20],
[41, 56]])
$$
A \cdot B=
\left(
\begin{array}{cc}
3 & 2& 1\\
6 & 5 & 4
\end{array}
\right)
\cdot
\left(
\begin{array}{cc}
1 & 2\\
3 & 4\\
5 & 6
\end{array}
\right)
$$
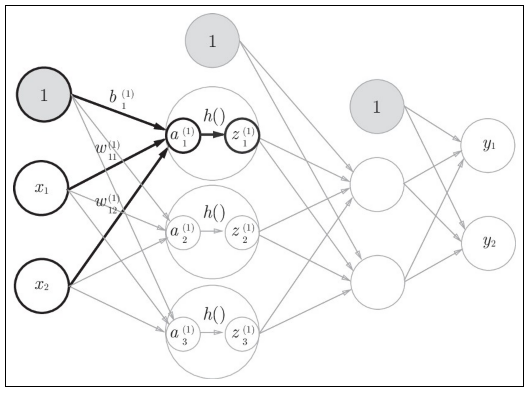
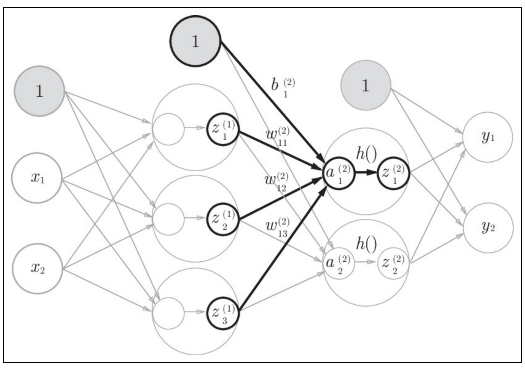
3層ニューラルネットワークの実装
入力層から第1層への信号の伝達
x = np.array([1., .5])
W1 = np.array([[.1, .3, .5], [.2, .4, .6]])
B1 = np.array([.1, .2, .3])
print('入力信号x=', x)
print('重みW1=', W1)
print('バイアスB1=', B1)
入力信号x= [ 1. 0.5]
重みW1= [[ 0.1 0.3 0.5]
[ 0.2 0.4 0.6]]
バイアスB1= [ 0.1 0.2 0.3]
x.shape, W1.shape
((2,), (2, 3))
x, W1の次元の要素数を合わせる!
A1 = np.dot(x, W1) + B1; A1
array([ 0.3, 0.7, 1.1])
隠れ層での重み付き和(重み付き信号とバイアスの総和)を$a$で表す。
Z1 = sigmoid(A1); Z1
array([ 0.57444252, 0.66818777, 0.75026011])
活性化関数で変換された信号を$z$で表す。
sigmoid関数が図中の$h$()にあたる。
第1層から第2層への信号の伝達
W2 = np.array([[.1, .4], [.2, .5], [.3, .6]])
B2 = np.array([.1, .2])
print('W2=', W2)
print('B2=', B2)
W2= [[ 0.1 0.4]
[ 0.2 0.5]
[ 0.3 0.6]]
B2= [ 0.1 0.2]
A2 = np.dot(Z1, W2) + B2; A2
array([ 0.51615984, 1.21402696])
Z2 = sigmoid(A2); Z2
array([ 0.62624937, 0.7710107 ])
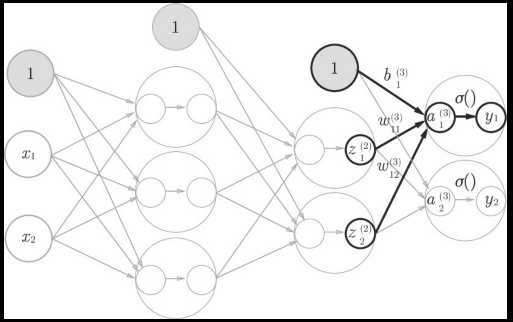
第2層から出力層への信号の伝達
def identity_function(x):
"""恒等関数と呼ばれる、入力をそのまま出力する、何もしない関数"""
return x
W3 = np.array([[.1, .3], [.2, .4]])
B3 = np.array([.1, .2])
print('W3=', W3)
print('B3=', B3)
W3= [[ 0.1 0.3]
[ 0.2 0.4]]
B3= [ 0.1 0.2]
A3 = np.dot(Z2, W3) + B3
Y= identity_function(A3); Y
array([ 0.31682708, 0.69627909])
identity_function()という関数を出力層の活性化関数として利用する。
出力層の活性化関数は$\sigma$()で表し、隠れ層の活性化関数$h$()とは区別する。
実装まとめ
def init_network():
"""重みとバイアスの初期化"""
network = {}
network['W1'] = np.array([[.1, .3, .5], [.2, .4, .6]])
network['W2'] = np.array([[.1, .4], [.2, .5], [.3, .6]])
network['W3'] = np.array([[.1, .3], [.2, .4]])
network['b1'] = np.array([.1, .2, .3])
network['b2'] = np.array([.1, .2])
network['b3'] = np.array([.1, .2])
return network
def forward(network, x):
"""入力信号が出力へと変換されるプロセス"""
W1, W2, W3 = network['W1'], network['W2'], network['W3']
b1, b2, b3 = network['b1'], network['b2'], network['b3']
# 入力層
a1 = np.dot(x, W1) + b1
z1 = sigmoid(a1)
# 隠れ層
a2 = np.dot(z1, W2) + b2
z2 = sigmoid(a2)
# 出力層
a3 = np.dot(z2, W3) + b3
return identity_function(a3)
x
array([ 1. , 0.5])
network = init_network()
x = np.array([1., .5])
forward(network, x)
array([ 0.31682708, 0.69627909])
3.5 出力層の設計
ソフトマックス関数
$$y_k = \frac{\exp{(a_k)}}{\sum_{i=1}^n\exp{(a_i)}}$$
def softmax(a):
"""入力値aを確率で返す"""
exp_a = np.exp(a - np.max(a)) # オーバーフロー対策
return exp_a/ np.sum(exp_a)
あまりに大きな値はinf="無限大"になって(オーバーフローと呼ぶ。)天井打ちしてしまい、正確な計算ができない。
そのため、以下に示すように数学的に等価となるように、$e^a$を小さい値に直してから合計値で割る。
$$
\begin{align}
y_k = \frac{\exp{(a_k)}}{\sum_{i=1}^n \exp{(a_i)}}
&= \frac{C\exp{(a_k)}}{C\sum_{i=1}^n \exp{(a_i)}}\\
&= \frac{\exp{(a_k+\log C)}}{\sum_{i=1}^n\exp{(a_i+\log C)}}\\
&= \frac{\exp{a_k + C'}}{\sum_{i=1}^n \exp{(a_i + C')}}
\end{align}
$$
上で説明していることは、つまりは$e^{a_k}$にどんな値を足しても、それを足し算した分母も同じ値足してやれば$y_k$の値に変化はないということ。
softmax(np.array([.3, 2.9, 4.]))
array([ 0.01821127, 0.24519181, 0.73659691])
データセットの取り出し
import os, sys
sys.path.append(os.pardir) # 親ディレクトリappend
from dataset.mnist import load_mnist
以下を実行するとmnistデータセットを.gzファイルをダウンロードし、解凍してからpklファイルに納める。
終わるのに数分を要する。
(x_train, t_train), (x_test, t_test) = load_mnist(flatten=True, normalize=False)
MNIST画像の表示
ソースはch03.mnist_show.py
.BMP形式で画像が表示される。
# %load mnist_show.py
import sys, os
sys.path.append(os.pardir) # 親ディレクトリのファイルをインポートするための設定
import numpy as np
from dataset.mnist import load_mnist
from PIL import Image
def img_show(img):
pil_img = Image.fromarray(np.uint8(img))
pil_img.show()
(x_train, t_train), (x_test, t_test) = load_mnist(flatten=True, normalize=False)
img = x_train[0]
label = t_train[0]
print(label) # 5
print(img.shape) # (784,)
img = img.reshape(28, 28) # 形状を元の画像サイズに変形
print(img.shape) # (28, 28)
img_show(img)
5
(784,)
(28, 28)
ニューラルネットワークの推論処理
# %load neuralnet_mnist.py
import sys, os
sys.path.append(os.pardir) # 親ディレクトリのファイルをインポートするための設定
import numpy as np
import pickle
from dataset.mnist import load_mnist
from common.functions import sigmoid, softmax
def get_data():
"""学習データのロード"""
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, flatten=True, one_hot_label=False)
return x_test, t_test
def init_network():
"""sample_weight.pklに保存された学習済み重みパラメータの読み込み"""
with open("sample_weight.pkl", 'rb') as f:
network = pickle.load(f)
return network
def predict(network, x):
"""neuralnetworkの実装
出力層が恒等関数ではなく
ソフトマックス関数になっている。"""
W1, W2, W3 = network['W1'], network['W2'], network['W3']
b1, b2, b3 = network['b1'], network['b2'], network['b3']
a1 = np.dot(x, W1) + b1
z1 = sigmoid(a1)
a2 = np.dot(z1, W2) + b2
z2 = sigmoid(a2)
a3 = np.dot(z2, W3) + b3
y = softmax(a3)
return y
%%timeit
x, t = get_data()
network = init_network()
accuracy_cnt = 0
for i in range(len(x)):
y = predict(network, x[i])
p= np.argmax(y) # 最も確率の高い要素のインデックスを取得
if p == t[i]:
accuracy_cnt += 1
print("Accuracy:" + str(float(accuracy_cnt) / len(x)))
Accuracy:0.9352
Accuracy:0.9352
Accuracy:0.9352
Accuracy:0.9352
1 loop, best of 3: 1.25 s per loop
バッチ処理
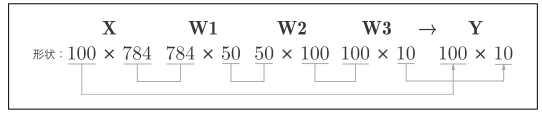
バッチ処理における配列の形状の推移
バス帯域の負荷を軽減する、すなわち、データの読み込みに対して演算の割合を多くするバッチ処理によって1枚当たりの処理時間を短縮できる。
大きな配列を読み込み、一度に大きな配列を計算するほうが、分割された小さな配列を少しずつ計算するよりも演算の終了が早い。
%%timeit
# %load neuralnet_mnist_batch.py
x, t = get_data()
network = init_network()
batch_size = 100 # バッチの数
accuracy_cnt = 0
for i in range(0, len(x), batch_size):
x_batch = x[i:i+batch_size]
y_batch = predict(network, x_batch)
p = np.argmax(y_batch, axis=1)
accuracy_cnt += np.sum(p == t[i:i+batch_size])
print("Accuracy:" + str(float(accuracy_cnt) / len(x)))
Accuracy:0.9352
Accuracy:0.9352
Accuracy:0.9352
Accuracy:0.9352
1 loop, best of 3: 269 ms per loop
バッチ処理によって約5倍速く実行できた。