はじめに

世の中に正しい実装のベイズ線形回帰があまり無いこと、入力が多次元に対応している実装が少ない点が気になり、使いやすいクラスとして実装をしました。記述は基本的にPRMLに従っています。

実装したクラス

といっても、実装っていうほど大したものじゃなくて、50行程度ですが・・
クラスの全体をここに書いておきます。もっている機能は下記の通りです。
すごくシンプルです。

$\phi$, $t$の組み合わせを与えて、事後分布を計算する
ベイズ線形回帰の、平均と共分散パラメータのランダムサンプリングをする
$\phi$を与えて予測分布の平均と分散を出力する

Beyes_LR.py

import numpy as np
from scipy.stats import multivariate_normal

class BeyesLinearRegression:
    def __init__(self, mu, S, beta):
        self.mu = mu
        self.S = S
        self.beta = beta

    def calc_posterior(self, phi, t):
        S_inv = np.linalg.inv(self.S)

        if len(phi.shape) == 1:
            phi = phi.reshape(1, -1)
            t = t.reshape(1, 1)
        self.S = np.linalg.inv(S_inv + self.beta * phi.T @ phi)
        self.mu = self.S @ (S_inv @ self.mu + np.squeeze(self.beta * phi.T @ t))

    def sampling_params(self, n=1, random_state=0):
        np.random.seed(random_state)
        return np.random.multivariate_normal(self.mu, self.S, n)

    def probability(self, x):
        dist = multivariate_normal(mean=self.mu, cov=self.S)
        return dist.logpdf(x)

    def predict(self, phi):
        if len(phi.shape) == 1:
            phi = phi.reshape(1, -1)
        pred = np.array([self.mu.T @ _phi for _phi in phi])
        S_pred = np.array([(1 / self.beta) + _phi.T @ self.S @ _phi for _phi in phi])

        # Above is a simple implementation.
        # This may be better if you want speed.
        # pred = self.mu @ phi.T
        # S_pred = (1 / self.beta) + np.diag(phi @ self.S @ phi.T)
        return pred, S_pred

全コードはgitにもおいてあります。（といっても50行程度です)

GitHub

ベイズ線形回帰について

式の導出等は下記が詳しいので、詳細は書きません。

事後分布の計算

重要なのは下記のように分布を更新していくということです。平たく書くと、$\phi$が説明変数、$t$が答えです。それに応じて、平均と共分散行列が更新されます。

$$M_N=S_N(S_0^{-1}m_0+\beta\Phi^Tt)$$

$$S_N^{-1}=S_0^{-1}+\beta\Phi^T\Phi$$

予測分布

予測分布は下記で表されます。こちらも詳細は割愛するけど、要は新しい点$x$に対して、下のような平均と分散で分布が表されるということ。

$$N(m_N^T\phi(x), 1/\beta+\phi(x)^TS_N\phi(x))$$

実装したクラスを使う

ここから実際に実装したクラスを使って、ベイズ線形回帰を試してみます。
僕が作成したクラスは、$x$から特徴量として作った$\phi$を与える必要があります。よくある実装だと、$\phi$の生成部分（例えば多項式）もクラス内に取り込まれていて、ベイズ線形回帰をしているのか、多項式によって特徴量設計しているのかがわかりづらかったりしますが、ここでは分離しています。

ということで、元データ$x$, $y$を入力し、あとは$\phi$を作る関数を実装してやれば基本的にはOKです。

sin波データでの回帰

Toyデータでまずはやってみます。

データの生成と特徴量関数の設計

入力データは、sin波の真の分布にノイズを乗せ、観測データとします。また、特徴量の関数の設計としては、いくつかの周波数の三角関数の合成波とします。メソッドのx_to_phiは10個の波をベクトル化しており、_phiは合成波を表しています。振幅がベイズ線形回帰で求めるパラメータになります。数式的には下記のイメージ。（よく考えたら第1項はゼロですね・・いらないわ・・）

$$y=w_1sin(0)+w_2sin(2\pi x)+w_3sin(2\times2\pi x)+\cdots+w_9sin(9\times2\pi x) $$

def x_to_phi(x):
    if len(x.shape) == 1:
        x = x.reshape(-1, 1)
    return np.concatenate([np.sin(2 * np.pi * x * m) for m in range(0, 10)], axis=1)


def _phi(x, params):
    return np.array([p * np.sin(2 * np.pi * x * i) for i, p in enumerate(params)]).sum(axis=0)

実際のデータ生成部分はこちら。

x = np.arange(0, 1, 0.01)
phi = x_to_phi(x)

e = np.random.randn(len(x)) / 10
y_true = np.sin(2 * np.pi * x)
y = y_true + e

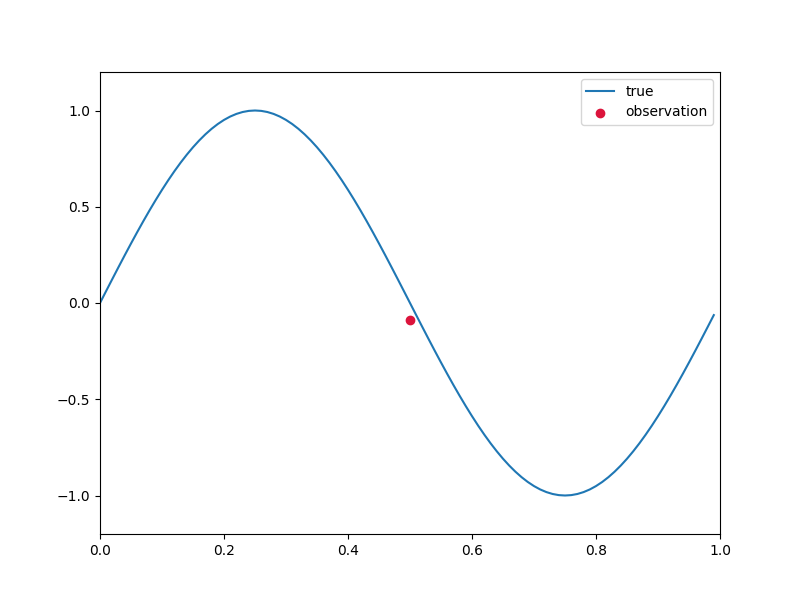
1点だけ観測した場合

まずは50番目のデータ1点だけが観測された場合を考えます。

train_idx = 50
x_train = x[train_idx]
phi_train = phi[train_idx]
y_train = y[train_idx]
plt.scatter(x_train, y_train, c='crimson', marker='o', label='observation')
plt.plot(x, y_true, label='true')

このデータに対して、早速事後分布を計算してやりましょう。
学習するだけなら、下記のように1行です。

# ベイズ線形回帰の初期値
input_dim = phi.shape[1]
mu = np.zeros(input_dim)
S = np.identity(input_dim)
sigma = 0.1
beta = 1.0 / (sigma ** 2)

# モデルの定義と学習
beyes_linear_model = BeyesLR.BeyesLinearRegression(mu, S, beta)
beyes_linear_model.calc_posterior(phi_train, y_train)

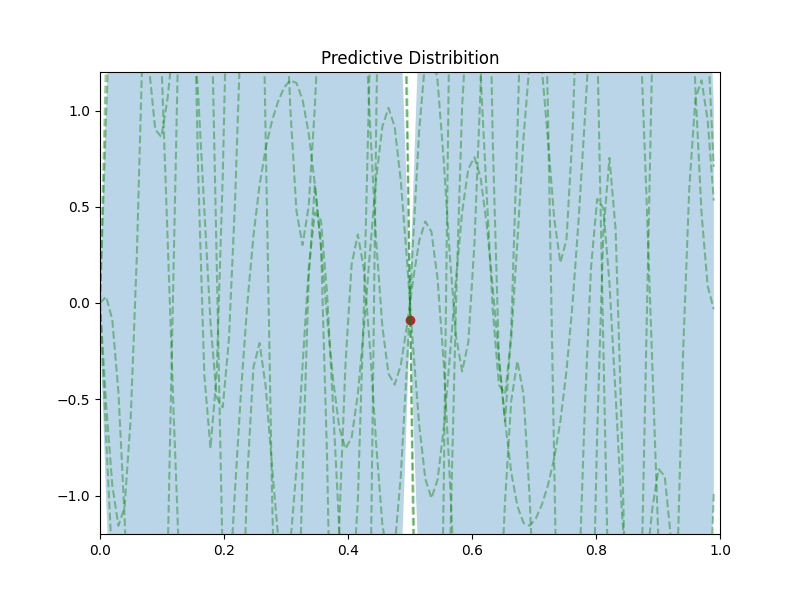
学習後の事後分布からランダムでいくつかサンプリングした波形を緑の点線で、予測分布を薄い青で表示します。
1点しか学習していないので、ほとんどが青色になっています。

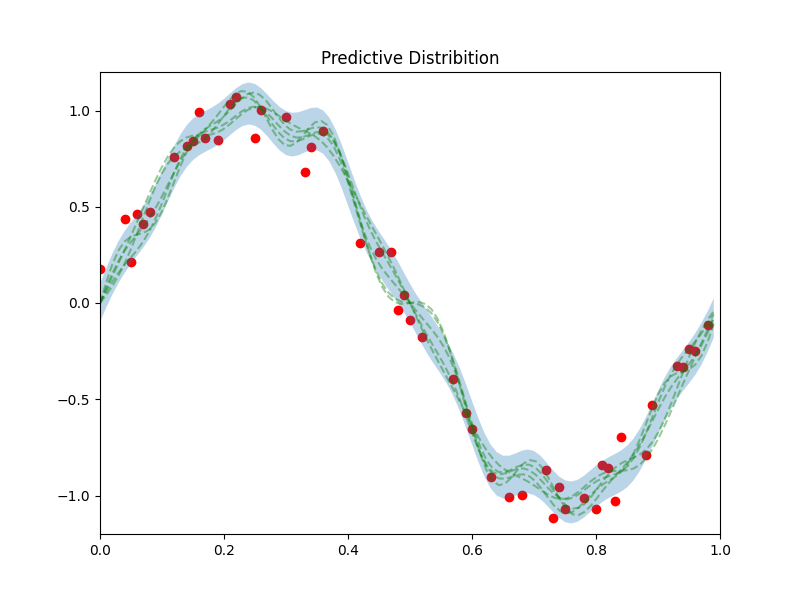
50点観測した場合

まったく同様のことを50点の観測データからやってみます。コードの違いとしては、train_idxをランダムで50個選んであげるだけです。
結果の予測分布は下記の図のようになります。

Advertisingデータセットでの回帰

次は実際の問題で、それも多次元の線形回帰を解いてみます。
多次元で更に特徴抽出をすると次元が増えすぎてわかりづらくなるので、$\phi$はLinearの関数とします。

入力データ

ISLRでもおなじみのAdvertisingデータセットです。
今回は入力としてTV, Radioの広告費、responseとして売上とします。

今回の$\phi$は線形なので、切片の項を付け加えてあげるだけです。回帰の式としては下記のような形になります。
$$Sales = w_0+w_1TV+w_2Radio$$

def x_to_phi(x, typ='linear', degree=3):
    if len(x.shape) == 1:
        x = x.reshape(-1, 1)
    return np.concatenate([np.ones(x.shape[0]).reshape(-1, 1), x], axis=1)


df = pd.read_csv(ADVERTISING_DATASET)
x = df[['TV', 'Radio']].values
y = df['Sales'].values

phi = x_to_phi(x)
x_train, x_test, phi_train, phi_test, y_train, y_test = \
    train_test_split(x, phi, y, train_size=0.05, random_state=0)

あとは前例と同様に学習してあげるだけです。

input_dim = phi.shape[1]
mu = np.zeros(input_dim)
S = np.identity(input_dim)
sigma = 10
beta = 1.0 / (sigma ** 2)

beyes_linear_model = BeyesLR.BeyesLinearRegression(mu, S, beta)
beyes_linear_model.calc_posterior(phi_train, y_train)

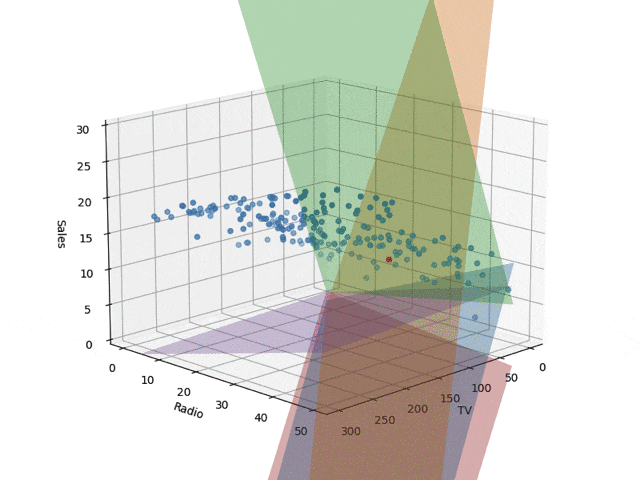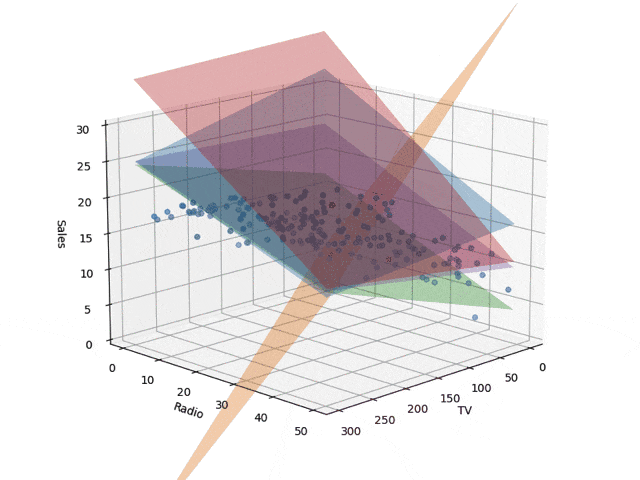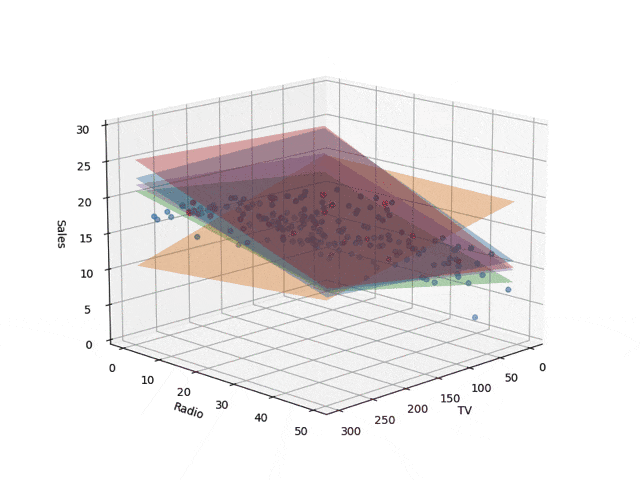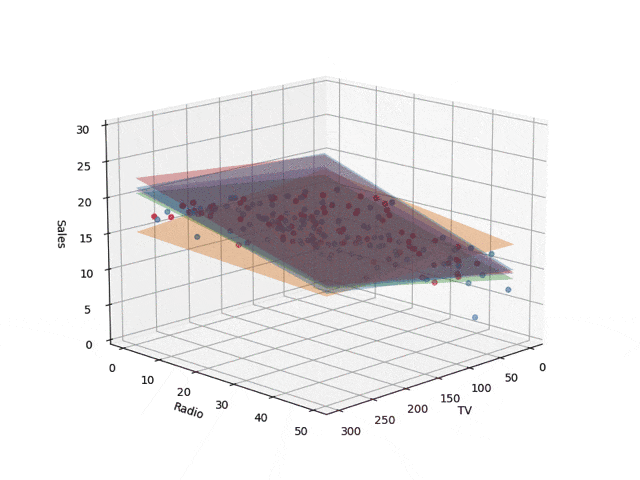
コードではtrain_sizeを0.05としていますが、これを変えながら描いた回帰面が下記です。ベイズ線形回帰で学習し、ランダムサンプリングで5平面を取り出して描画したものです。学習サンプル数が少ないとでたらめな
平面が描かれますが、データ点が増えていくにつれて収束していきます

おわりに

最後に少しだけベイズ線形回帰の宣伝を。
まだ理解が足りていない部分もありますが、ベイズ線形回帰の特徴抽出関数$\phi$の設計が重要になってきます。ここを陽に書き下さず、分散共分散行列を、カーネル関数を用いて計画行列として取り扱うのがガウス過程回帰だと認識しています。
しかし、もし良い特徴量が抽出できる事前知識があれば、説明性の観点においても、ベイズ線形回帰でも充分なことが経験上多いです。また、ベイズ線形回帰はその計算方法上、逐次学習もそのままできます。計算した事後分布を事前分布として学習していけばいいだけです。ガウス過程回帰のようにグラム行列の再計算もしなくて済みます。オンライン版もあるのでしょうけど・・

さてさて、ぜひ快適なベイズ線形回帰ライフを！

ベイズ線形回帰クラスのpython実装