ニューラルネットワークの超基礎的な動きを理解する

はじめに

最近のデータサイエンティストの方や、Deep全盛の時代（それほどでもない？）に機械学習を始めた方は、そもそも基本的なニューラルネットワークの動作を理解していない人も多いと思います。今回は簡単な例題について、ニューラルネットワークの学習過程を可視化して、どんな動きをしているのかを見てみます。もちろん、自分自身の勉強も兼ねて・・

最初に申し上げますが、詳しい方には物足りません。
だけど、基礎的なことは何回勉強してもタメになります。

ニューラルネットワークってなにやってるの？

Deepになって、非線形性がどうのこうのとか聞きますが、Deepであることと非線形は関係がありません。ニューラルネットワークを非線形たらしめているのは、活性化関数$f$です。線形変換は何回繰り返しても線形です。よく考えてみましょう。

基本的な全結合ニューラルネットワークは下記のような式です。

Y = f(WX + B)

例えば2層分書くとこうなります。

Y = f(W_2f(W_1X + B_1) + B_2)

当たり前ですが、$WX+B$という線形変換を行い、$f$という非線形の活性化関数を通しています。
ここで、$f$が非線形関数ではなく、単純な恒等変換だとすると、当然こうなります。

Y = WX + B

2層分だと下記の通り。

Y = W_2(W_1X + B_1) + B_2 = W_2W_1X + W_2B_1 + B_2\\
Y = WX + B\\
where\ W = W_2W_1, B = W_2B_1 + B_2

仮に$W$が正方行列（次元を上げ下げしない）とすると、みなさんご存知、回転や平行移動、拡大縮小を行う関数です。つまり、入力データを回転したり平行移動したり拡縮することでデータを動かしています。それだけです。何層積み重なってもそれだけです。

ではここに活性化関数$f$が入ると何が起きるでしょうか。平たく書けば、上記変換に加えて、伸縮が入ります。移動、回転、拡縮、伸縮をさせたりしながら、入力データを動かしています。

ニューラルネットワークの分類問題って具体的には何やってるの？

ニューラルネットワークを用いて2分類問題を考えてみましょう。
超シンプルなニューラルネットワークを考えます。

最終層には分類問題でおなじみのSoftmax関数があるとします。

y_i=\frac{e^{x_i}}{\sum_{k} e^{x_k}}\\
\sum_{i} y_i=1

Softmax関数は数式だと上記の通りですが、2つ目の式は2次元で考えれば、$y_1+y_2 = 1$です。図で書けば下記の青い線です。

さて、機械学習で分類問題を考えるとき、決定境界と呼ばれる境界線を考えます。この青い線の上に乗っているデータ点を分ける方法をどう考えるでしょうか。大抵の人であれば、これに垂直な線を引いて分けようと考えるはずです。

赤い境界線を引きました。これは、$y1$と$y2$の値の大きなほうを予測クラスとして採用するイメージです。水色に落ちた点はclass1、オレンジに入った点はclass2として分類されるわけです。

前の項で説明した、入力データを平行移動、回転、伸縮をさせて、最後はこういう青い線の上に点を落としていき、それに垂直な赤い線で色分けが出来ればめでたく分類ができるというわけです。

実例紹介

ここからは3種類のデータに対して、実例をお見せしていきます。

線形分離可能問題

入力データとモデル構成

一番シンプルな、線形分離が可能な問題を見てみましょう。
直線を引けば一発で解ける問題です。

学習の様子

下記のようなモデルで、解いてみます。学習と決定境界の様子はこちらです。ちゃんと線を引けていますね。

Layer	ノード数	活性化関数
1	2	linear
2	2	softmax

角層の出力も可視化してみましょう。冒頭で述べたように、回転・平行移動・拡大縮小を行って、青と赤がうまく分かれるように移動させています。いま、決定境界線は黒い点線で描いています。

線形分離できない問題

入力データ　その１

皆さんご存知のスイスロール(簡易版)です。
これを線形分離のときと同じニューラルネットワークで解いてみます。

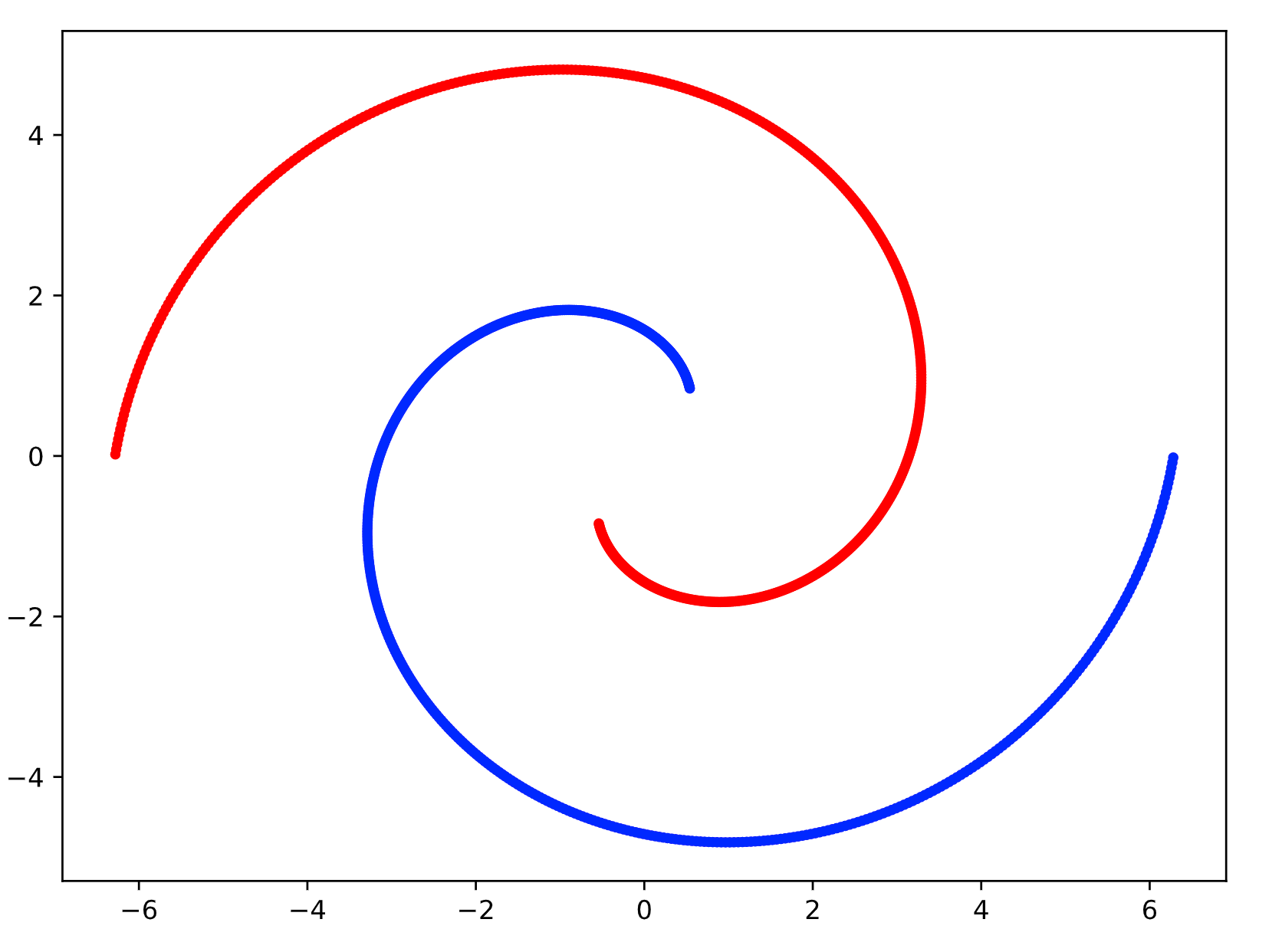
2層の場合（線形）

Layer	ノード数	活性化関数
1	2	linear
2	2	softmax

いくら学習しても、直線しか引けませんので当然分離しません。一番コストが低くなる線までは学習されます。

2層の場合（非線形）

活性化関数を$\tanh$にしてみます。
するとしっかりと学習されることがわかります。

Layer	ノード数	活性化関数
1	2	tanh
2	2	softmax

ただし、学習の収束に時間がかかったり、境界線にも無理があったりするように見えます。これはモデルの自由度（パラメータ数）が低く、データにフィットするためのモデルの複雑さが少し足りていないように見えます。

6層の場合（非線形）

少し層を増やしてみます。
あっという間に収束し、しっかりと分類ができています。この程度の規模であればニューラルネットワークは決してブラックボックスではなくて、入力データをこねくりまわすことで、最終的に決定境界を作っている様子がよくわかると思います。

Layer	ノード数	活性化関数
1	2	tanh
2	2	tanh
3	2	tanh
4	2	tanh
5	2	tanh
6	2	softmax

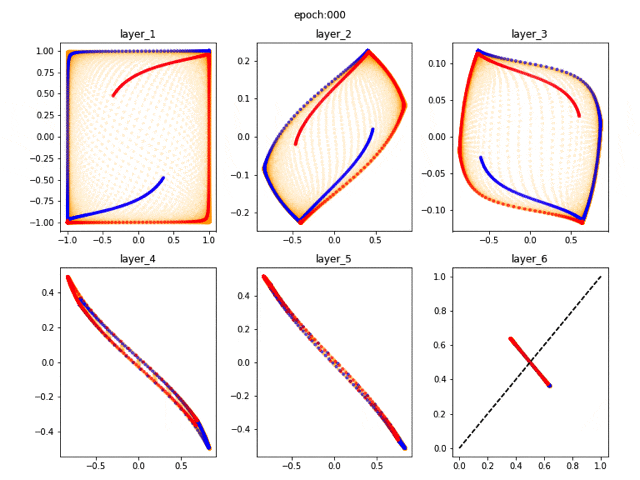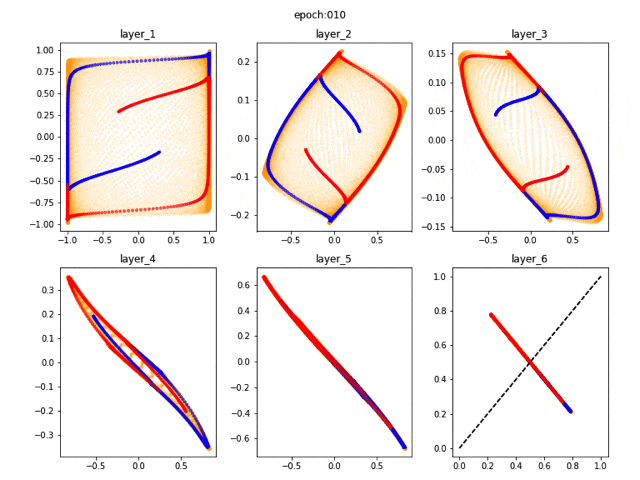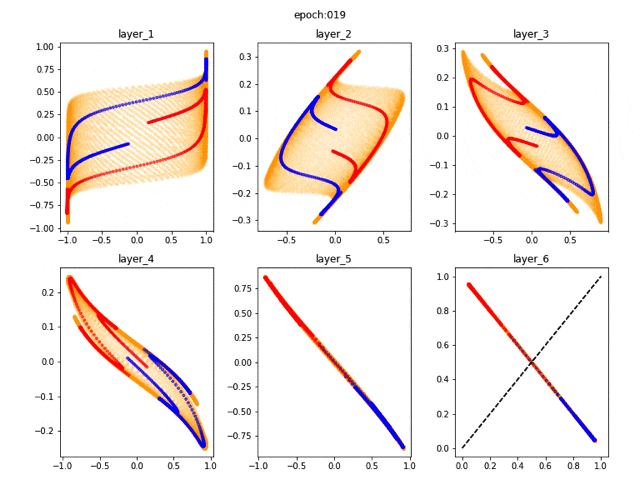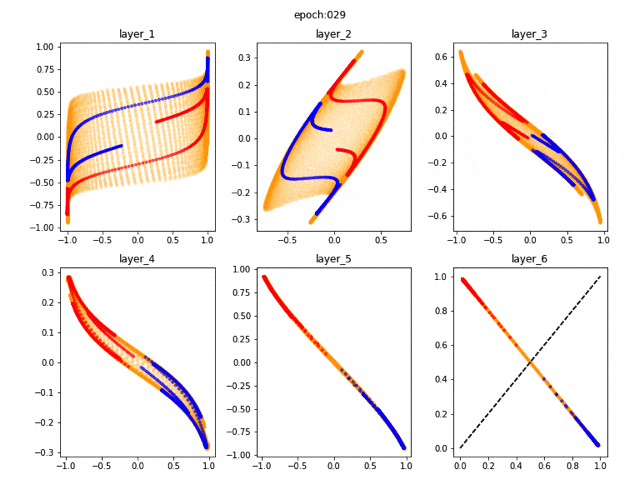
2層で次元を増やした場合（非線形）

パラメータ数を増やすには、層を増やすというパターンと、次元を増やすというパターンがあります。そもそも中間層の次元を増やすというのはどういうことでしょうか。

仮に、2→3→2というような、中間層が膨らんだニューラルネットワークを考えることにします。活性化関数を除くと、下記のような演算がされます。$i$は角層の入力、$o$は角層の出力のつもりです。

    \left(
        \begin{array}{ccc}
            o_1\\
            o_2\\
            o_3
        \end{array}
    \right)
    =
    \left(
        \begin{array}{ccc}
            w_{11} & w_{12} \\
            w_{21} & w_{22} \\
            w_{31} & w_{32}
        \end{array}
    \right)
    \left(
        \begin{array}{ccc}
            i_1\\
            i_2
        \end{array}
    \right)\\
    \left(
        \begin{array}{ccc}
            o_1\\
            o_2\\
            0
        \end{array}
    \right)
    =
    \left(
        \begin{array}{ccc}
            w_{11} & w_{12} & w_{13} \\
            w_{21} & w_{22} & w_{23} \\
            0 & 0 & 0
        \end{array}
    \right)
    \left(
        \begin{array}{ccc}
            i_1\\
            i_2\\
            i_3
        \end{array}
    \right)

第1式は次元を持ち上げる演算です。第2式は3次元から2次元への射影となります。その射影される面も、持ち上げる方法もパラメータとして学習されます。つまりどう持ち上げて、どの角度から射影すればうまく分離するか、が学習されるわけです。

これなら分離がよくなる気がしてきますね。
実際に試してみましょう。

Layer	ノード数	活性化関数
1	10	tanh
2	2	softmax

GIFの冒頭で島のような領域ができるのは、高次元から低次元へ射影が行われるからです。

入力データ　その２

最後にドーナツ状のデータを見てみましょう。

2層の場合（非線形）

ドーナツデータを非線形で解くことは可能でしょうか。
直感的にも、島を作るには次元を上げないとできない気がしますが、まさにその通りの結果となります。2次元上でいくら変形をしても飛び地を作ることは難しいようです。

Layer	ノード数	活性化関数
1	２	tanh
2	2	softmax

2層で次元を増やした場合（非線形）

次元を増やせば時間はかかりますが、うまくいきます。
直感的にも上述の通りで理解しやすいです。

Layer	ノード数	活性化関数
1	10	tanh
2	2	softmax

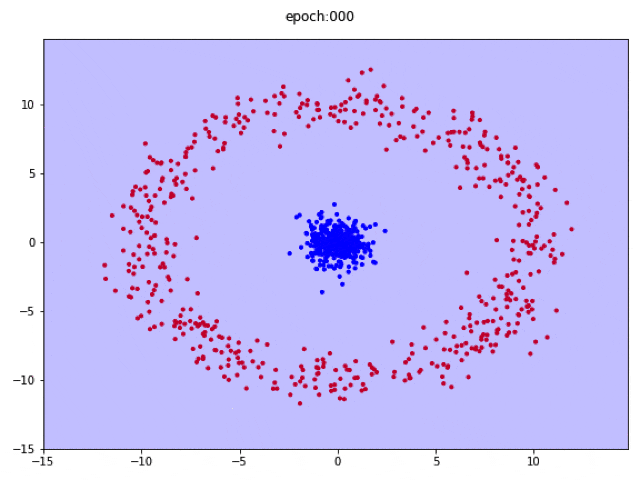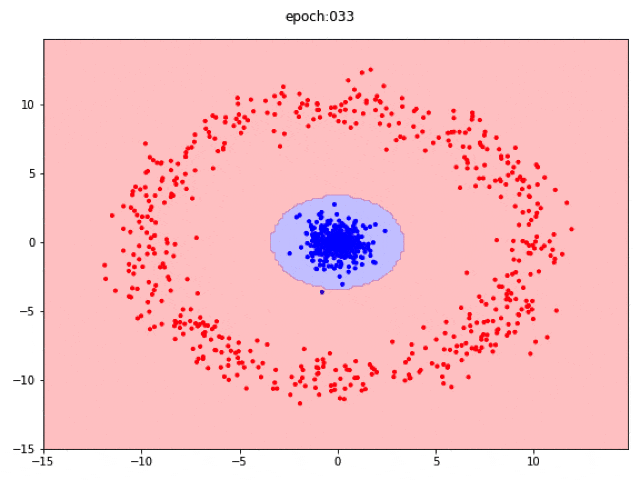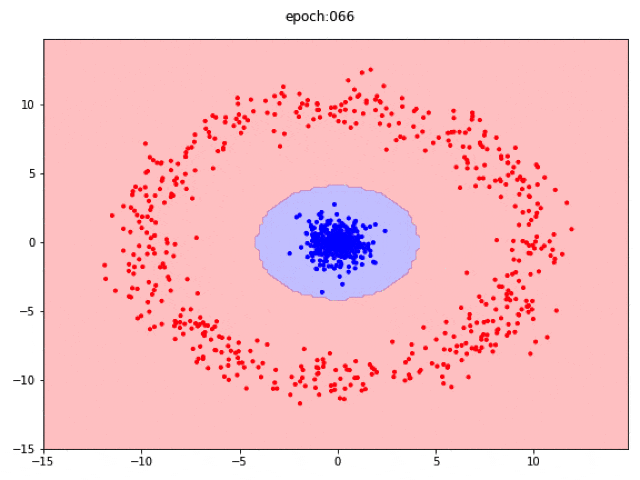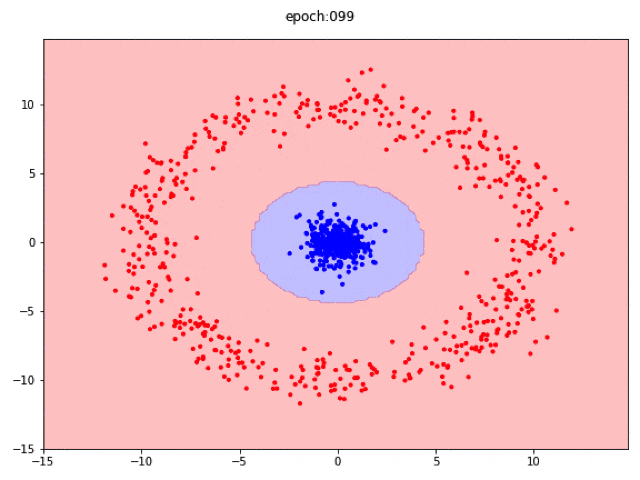
極座標でデータを考える

ただし、ドーナツ状のデータはどう見たって距離によってデータが変わります。なので$r, theta$というか、$r$だけでデータを線形分離したほうが遥かに賢いです。Toyデータなので、そういうツッコミは面白くないですが、わかっている知識はちゃんと使っておいたほうが賢いということです。

一応、入力を極座標として、線形ニューラルネットワークで分離する様子も置いておきます。

まとめ

ここまで眺めてみると、ニューラルネットワークの基本的な動きがよくわかったように思えるのではないでしょうか。ニューラルネットワークはブラックボックスだから、と突き放されたりしますが、少しでも身近な存在になれればと思います。

また、複雑なCNNなどはこんなにシンプルではありませんが、例えば最終層付近だけをFineTuningしたい、という場合は、今自分が何を構築しようとしているかを、ふと初等的に振り返ってみることも重要だと思います。

さいごに

３種類のデータを見てきましたが、特にスイスロールデータはTrainingデータへのFitは理解できましたが、境界線が人間の感覚とはずれているように感じます。
このあたり、もう少し賢く学習できないものでしょうか。良いアイデアが思いついたらまた更新したいと思います。