誰でも理解できるガウス過程とガウス過程回帰 実装編

はじめに

前回はガウス過程回帰の数式を追ってきました。今回はそれに基づいて実装を行っていきます。
全体の実装はクラス化して、Example付きでGitHubにおいてあります。
多次元にも対応しつつ書き下された実装は少ないので、多少レアかと思います。
動作検証という意味では、GPyと結果が定性的に一致することは確認済です。

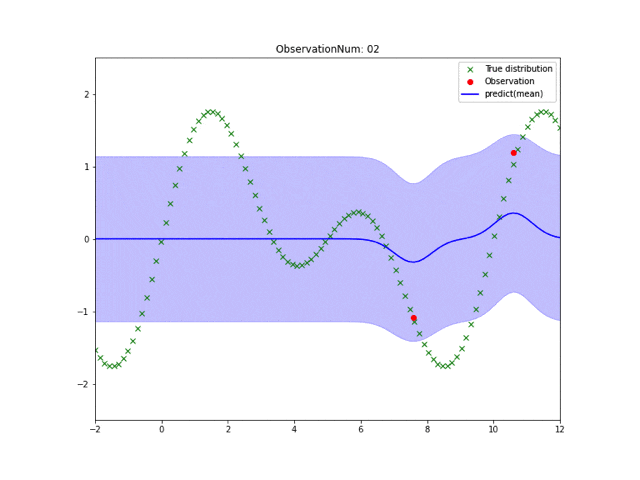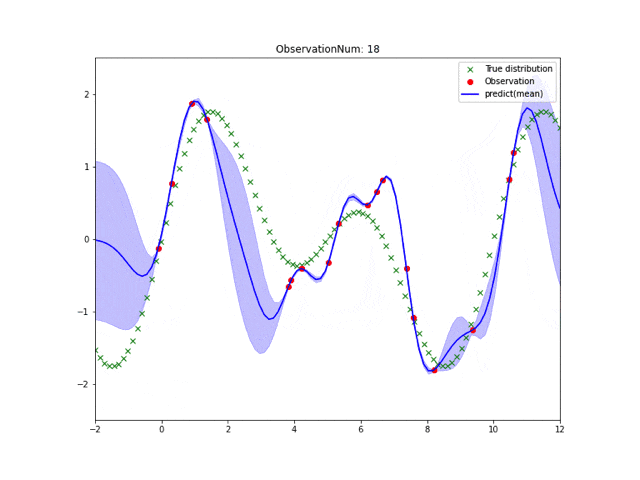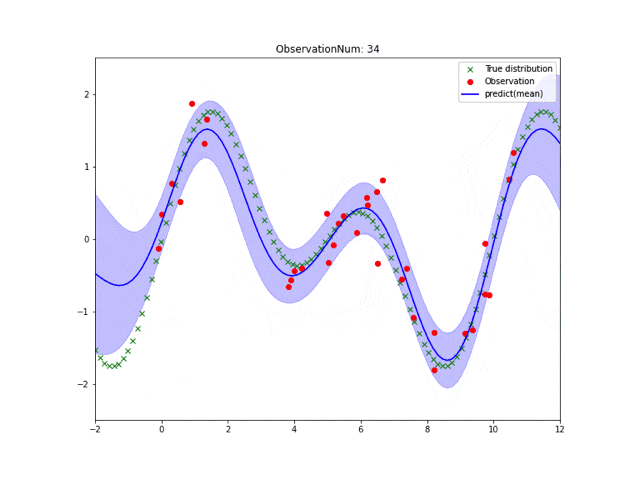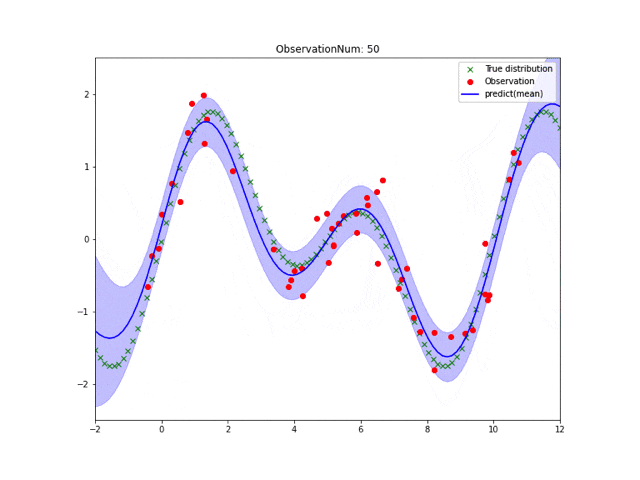
動かしてみる

実行結果は皆さん見慣れたこんな感じになります。

なんで実装すんの？

正直実装しなくてもいいです。
Gpyとか、便利なライブラリがあるので、それを利用したら一発で使えます。
あくまでも中身を理解したい人向け。

実装のポイント

実はガウス過程回帰は演算的には非常にシンプルです。
なんせグラム行列さえ計算できればほぼ終わりだからです。
ということでポイントを絞って書きます。
いろいろなブログで適当に触れられているハイパーパラメータ調整についても少し細かく記載します。

グラム行列

演算速度は気にせず、下記のような形で実装をしています。
実際は半分は計算がいらなかったり、工夫のしようはありますが、いまは理解をすることを優先しています。
x1, x2という配列が渡されると、その全組み合わせパターンを演算します。ただし対角成分（x1==x2)のときのみ、betaを足すようになっています。これは数式では$k(x,x')+\beta^{-1}\delta_{ij}$に対応しています。

self.kernel = self.__gaussian_kernel

def create_kernel_mtx(self, x1, x2):
    x1_ = self.__data_checker(x1)
    x2_ = self.__data_checker(x2)
    K = np.array(
        [self.kernel(_x1, _x2, np.all(_x1 == _x2)) for _x1 in x1_ for _x2 in x2_]
    )
    K = K.reshape(x1_.shape[0], x2_.shape[0])
    return K

def __gaussian_kernel(self, x, x_prime, delta):
    return np.squeeze(
        self.theta[0]
        * np.exp(-self.theta[1] / 2 * np.linalg.norm(x - x_prime) ** 2)
        + self.theta[2]
        + self.theta[3] * x.T @ x_prime
        + 1 / self.beta * delta
    )

@staticmethod
def __data_checker(x):
    if x.shape == ():
        x = x.reshape(1, 1)
    elif len(x.shape) == 1:
        x = x.reshape(-1, 1)
    return x

ハイパーパラメータ調整

ハイパーパラメータを調整するには、尤度$L$とその傾きを計算する必要があります。
そのため、各パラメータでの偏微分を下記のように計算します。
最適化そのものは、符号を逆にした尤度$-L$と傾きをscipyのminimizeに与えて最小化するようにしています。
ちなみにscipyのminimize関数は、jac引数をTrueにすることで、functionの戻り値に、(最小化したい対象、傾き）というTupleを渡すことが出来ます。jacはヤコビアンのヤコ、ですね。

def optimize(self):
    def __objective(_beta, _theta):
        self.set_parameters(_beta, _theta)
        Cn = self.create_kernel_mtx(self.x_train, self.x_train)
        Cn_inv = np.linalg.inv(Cn)
        partial_C = self.__partial_diff(self.x_train, self.x_train)
        L = np.array(
            -0.5 * np.linalg.slogdet(Cn)[1]
            - 0.5 * self.y_train.T @ Cn_inv @ self.y_train
            - 0.5 * len(self.x_train) * np.log(2 * np.pi)
        )

        dbeta = np.array(
            -0.5 * np.trace(Cn_inv) / (_beta ** 2)
            + 0.5 / (_beta ** 2) * (self.y_train.T @ Cn_inv @ Cn_inv @ self.y_train)
        )

        dtheta = np.array(
            [
                0.5 * np.trace(Cn_inv @ p_c)
                - 0.5 * self.y_train.T @ Cn_inv @ p_c @ Cn_inv @ self.y_train
                for p_c in partial_C.T
            ]
        )

        dL = np.append(dbeta, dtheta)
        return -L, dL

    old_beta = self.beta
    old_theta = self.theta
    param_bounds = self.param_bound
    result = minimize(
        x0=np.append(self.beta, self.theta),
        fun=lambda param: __objective(_beta=param[0], _theta=param[1:]),
        jac=True,
        bounds=param_bounds,
    )
    print("Optimize:: ", result.success)
    if result.success:
        self.set_parameters(result.x[0], result.x[1:])
    else:
        self.set_parameters(old_beta, old_theta)

def __partial_diff(self, x1, x2):
    def f_dtheta0(x, x_prime):
        return np.exp(-self.theta[1] / 2 * np.linalg.norm(x - x_prime) ** 2)

    def f_dtheta1(x, x_prime):
        _d = np.linalg.norm(x - x_prime) ** 2
        return -0.5 * _d * self.theta[0] * (np.exp(-0.5 * self.theta[1] * _d))

    def f_dtheta2(x, x_prime):
        return 1

    def f_dtheta3(x, x_prime):
        return x.T @ x_prime

    x1_ = self.__data_checker(x1)
    x2_ = self.__data_checker(x2)
    dtheta = np.array(
        [
            [
                f_dtheta0(_x1, _x2),
                f_dtheta1(_x1, _x2),
                f_dtheta2(_x1, _x2),
                f_dtheta3(_x1, _x2),
            ]
            for _x1 in x1_
            for _x2 in x2_
        ],
        dtype=np.float32,
    )
    return dtheta.reshape(x1_.shape[0], x2_.shape[0], 4)

まとめ

2回に分けてガウス過程の回帰を眺めてきました。
ガウス過程の仮定をおけるような問題の場合で、非線形モデリングをしたい場合にはパラメータも少なくとても強力なツールです。用法用量を守って正しく使っていきましょう。
高速に演算したいとか思ったら、普通にGPyとか使ってください。