はじめに
一世を風靡したGAN。いや、今もしていると言っても過言ではないGANです。今回は一番最初の論文に従ってこの目的関数を解いてみます。いろいろな場所で見るのですが、微妙に数式の間が省略されていたりしてわかりづらかったので、行間を埋めて解いていきたいと思います。
いまさら?と思った方は見なくていいです。
タイトルにも書いてあるとおり、いまさらです。
学習過程のおさらい
GANの学習過程について、元の論文では下記のような図を用いて説明しています。
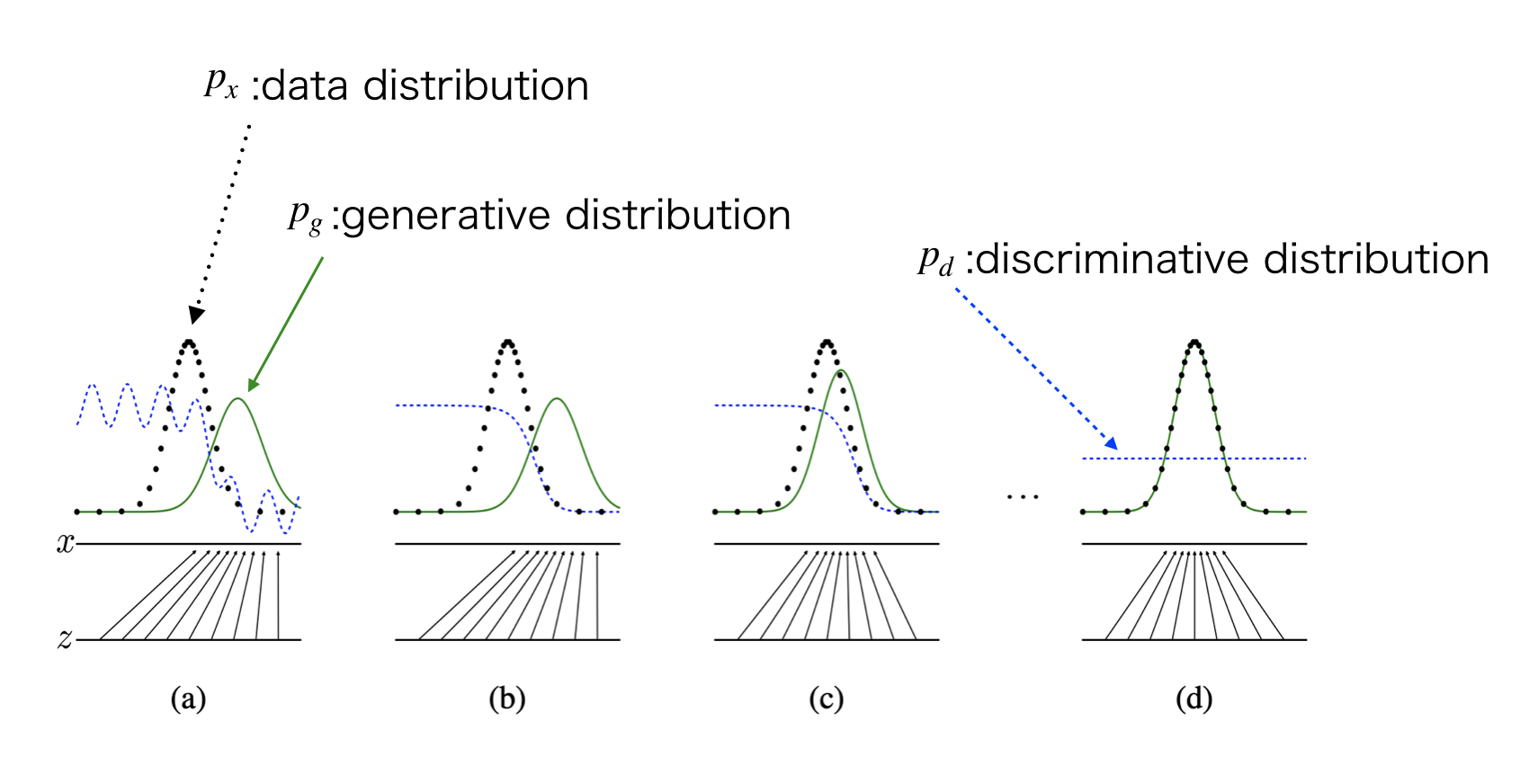
(a)は初期状態です。discriminatorの識別結果$p_d$はランダムで、generateされたデータの分布$p_g$も真のデータの分布$p_x$とは異なっています。
(b)ここからまずはdiscriminatorを学習していきます。そうすると、$p_x$と$p_g$をうまく分離するような$p_d$が学習されます。
(c)この後でgeneratorを学習します。そうすると$p_d$はgenerateされた分布と真のデータ分布うまく分離できなくなり、$p_x$と$p_g$が近づいていきます。
(d)この(b),(c)の作業を繰り返すことで、$p_x$と$p_g$がほぼ一致し、$p_d$では判別ができなくなり、$p_d$は0.5を返すようになる。という収束がGANの学習結果になります。
目的関数
さて、これを数式で考えてみましょう。とても有名なミニマックスの数式です。絵画のサインにも書かれましたね。まぁこの絵画が良いかどうかは別として・・
$$\min_G \max_D V(D,G) = \min_G \max_D \mathbb E_{x \sim p_{data}(x)}[\log{D(x)}]+ \mathbb E_{z \sim p_z(z)}[\log{(1-D(G(z)))}] \tag{1}$$
この式が論文ではさくっと登場します。その導出(というか考え方)は下記のようなものになるでしょう。
目的関数の導出
$D(x)$は、$x$が訓練データらしいかを0~1で判断します。$y$を正解ラベルとすると、正答の期待値は下記のように表されます。つまりこの$D$をパラメータ$\phi$を調整することで最大化してやれば、正答が最大化されるわけです。
$$E_{p(x,y)}[y\log D(x;\phi)+(1-y)\log(1-D(x;\phi))]$$
この同時確率を条件付き確率で記載します。
$$=E_{p(x|y)p(y)}[y\log D(x;\phi)+(1-y)\log(1-D(x;\phi))]$$
更に場合分けして書いてみます。
$$=E_{p(x|y=1)p(y=1)}[\log D(x;\phi)]+E_{p(x|y=0)p(y=0)}[\log(1-D(x;\phi))]$$
いよいよGANの目的関数に近づいてきます。$y=1$というのは真の分布から発生していることを示し、$y=0$というのは偽、つまりGenerateされた分布から発生していることを示すので、書き換えます。
$$\approx E_{p_{data}(x)}[\log D(x;\phi)]+E_{p_g(x)}[\log(1-D(x;\phi))]$$
ちなみに、ここまではGeneratorが登場しないので、$D$に関して最大化すれば良い問題です。ここで、$y=0$というデータ($x$から生成する$p_g(x)$)を、GANのようにノイズから作る$p_z(z)$と書き換えれば、有名な目的関数が得られます。
$$V(D,G)=E_{x\sim p_{data}(x)}[\log(D(x))]+E_{z\sim p_z(z)}[\log(1-D(G(z)))] \tag{2}$$
$G(z)$は$x$に近いデータを作成し、$D$を騙す役割を持ちます。$G(z)$の立場で言えば、自身の分布を変化させることで、この関数を最小化して、正答率を下げようとするのが目的です。
そもそも以上で書いたことは、目的関数を見れば自明である。と数学に明るい人は言うんだけれど、僕は最初全然わからなかったので書いてみた限りです。
Dの学習
では最初の図の(b)に書いてある、$D$の学習をしていきましょう。$D$の立場で言えば、この関数を最大化させればいいわけです。$G$を固定すると、
$$V(D,G)=\int_x p_{data}(x)\log D(x)dx+\int_z p_z(z)\log(1-D(G(z)))dz$$
ここで$G(z)=x\sim p_g$と考えます。つまり、$D$に入るデータは、異なる2つの分布から作られているという、下記のようなイメージです。

そう考えると、上の式は下記のように変形が出来ます。
$$=\int_x \left\{ p_{data}(x)\log D(x)+p_g(x)\log(1-D(x)) \right\}dx \tag{3}$$
上記の積分記号の内側は下記のような形をしています。
$$f(x)=a\cdot \log(x)+b\cdot \log(1-x)\tag{4}$$
これが最大となる点を見つけるためには、微分して0になる点を考えればよいです。第2項の微分は高校生時代の合成関数の微分計算で解くことが出来ます。$y=\log(1-x),u=1-x$とおくと、$y=\log(u)$となり、
$$\frac{df}{dx}=\frac{df}{du}\frac{du}{dx}=\frac{1}{u}\cdot-1=\frac{1}{x-1}$$
この合成関数の微分を用いて(4)式を微分すると、
$$f'(x)=\frac{a}{x}+\frac{b}{x-1}$$
となります。これが0になる点が最大なので、
$$\frac{a}{x}+\frac{b}{x-1}=0$$
$$x=\frac{a}{a+b}$$
この知識を用いて(2)式に当てはめれば、この式を最大化する$D=D^\ast_G$は下記で表されます。
$$D^\ast_G=\frac{p_{data}(x)}{p_{data}(x)+p_g(x)} \tag{5}$$
Gの学習
$V(G,D)$が最大となる$D$を見つけたので、それを使って、$V$を計算し、$G$を考えていきます。(5)式を、(2)式へ代入してあげます。
$$V(G,D^\ast_G)=E_{x \sim p_{data}}[\log(D^\ast_G(x))]+E_{z \sim p_z}[\log(1-D^\ast_G(G(z)))]$$
$$=E_{x\sim p_{data}}[\log(D^\ast_G(x))]+E_{x\sim p_g}[\log(1-D^\ast_G(x))]$$
$$=E_{x\sim p_{data}}[\frac{p_{data}(x)}{p_{data}(x)+p_g(x)}]+E_{x\sim p_g}[\frac{p_g(x)}{p_{data}(x)+p_g(x)}] \tag{6}$$
この(6)式の第1項を変形してみましょう。
$$E_{x\sim p_{data}}[\frac{p_{data}(x)}{p_{data}(x)+p_g(x)}]=E_{x\sim p_{data}}[\log(\frac{p_{data}(x)} {\frac{p_{data}(x)+p_g(x)}{2}}\cdot\frac{1}{2})]$$
$$=E_{x\sim p_{data}}[\log(\frac{p_{data}(x)} {\frac{p_{data}(x)+p_g(x)}{2}})+\log(\frac{1}{2})]$$
$$=-\log2+E_{x\sim p_{data}}[\log(\frac{p_{data}(x)} {\frac{p_{data}(x)+p_g(x)}{2}})]$$
$$=-\log2+KL(p_{data}||\frac{p_{data}+p_g}{2})$$
第2項も同様に計算が出来ます。これを合わせて、下記の式を導くことができます。
$$\therefore V(G,D^\ast_G)=-\log4+KL(p_{data}||\frac{p_{data}+p_g}{2})+KL(p_g||\frac{p_{data}+p_g}{2})$$
$$=-\log4+2JS(p_{data}||p_g)$$
$$\because JS(P||Q)=\frac{1}{2}KL(P||M)+\frac{1}{2}KL(Q||M)\hspace{20pt}M=\frac{P+Q}{2}$$
つまり、$V$が$D$により最大化された状態で、$V$を最小化するための$G$というのは、このJS divergenceを最小化することに尽きます。結局は$p_{data}$と$p_g$の分布を近づけることが目標となるわけです。逆に言えば、このような目的関数のminmax問題を解くことで分布を近づけることができるというわけです。
まとめ
いろいろと書きましたが、Generateされた分布と入力されたデータの分布を近づけるということが重要なんだと思います。それを利用したGANの応用が昨今わんさかと発表されています。Domain Adaptationは試してみたいなぁ。
以上、今さら聞けないGANの目的関数でした。