動的計画法
動的計画法の一般的な形式は、最適値を求めることである。 動的計画法は、実はオペレーションズリサーチの最適化手法であるが、情報系では、より一般的に使われている。
最適値を求めるといっても、実は、動的計画法の核心問題は列挙である。微分積分や変分法の最適化と異なり、動的計画法に適応する問題では、最適値を求めるために、すべでの可能な答えをリストアップして、最適値を見つけ出さなければいけない。
然も、動的計画法はそうなに簡単で終わるはずがない。PaizaやLeetCodeの問題を見ればわかる。かなり大変であろう。
まず、動的計画法の列挙はちょっと特殊で、このタイプの問題では、「重複サブ問題」があるので、力任せ探索法を使うと、非常に効率が悪い。だからこそ、無駄な計算をしないようにするために「メモ」や「DPテーブル」が必要になる。
さらに、動的計画問題は、必ず「サブ構造(Substructure)最適化」問題をを持っている。このため、サブ問題の最適値によって元問題の最適値を求めることが可能になる。
また、動的計画法の核心となる考え方は、列挙を行うことであるが、問題があまりにも多様化しているため、すべての可能解を列挙することは容易ではない。正しい「状態伝達方程式」をリストアップして初めて、正しく列挙することが可能となる。
上述した「重複部分問題」、「部分構造最適化」、「状態伝達方程式」は、動的計画の3つの要素である。 それが何を意味するのかは、例を挙げて詳細に説明するが、実際のアルゴリズム問題では、状態遷移方程式を書くことが最も難しい。
以下、動的計画の基礎をフィボナッチ数列問題とお釣り問題を通してに詳しく説明する。 前者は「重複サブ問題」とは何かを理解してもらい(フィボナッチ級数は厳密には動的計画問題ではない)、後者は状態伝達方程式をどのようにリストアップするかのを説明する。
簡単な例だけであれば、アルゴリズムの背後にある一般的な考え方や技術に完全に集中することができ、曖昧な細部に惑わされることを避ける。
1 フィボナッチ数列
1.1 一般の再帰
フィボナッチ数列の数学的形式は再帰的であり、コードでの記述方法は以下の通り:
def fibonacci(n):
if n<2:
return n
else:
return fib1(n-1) + fib1(n-2)
言うまでもなく、再帰について話すとき、必ずこの例をとる。 このようなコードを記述することは簡潔で理解しやすいが、非常に非効率的である。 n = 20と仮定して、再帰木を描画します。
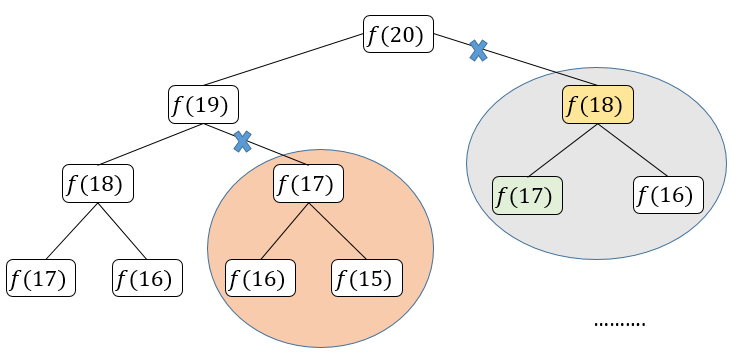
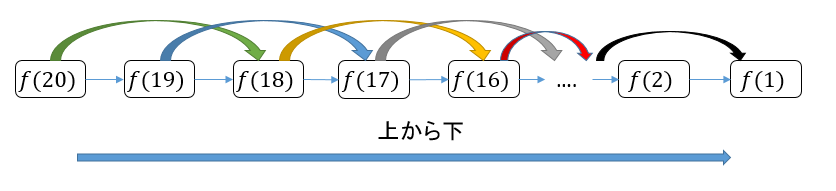
この再帰木を理解するにはどうすればよいか? つまり、元の問題 $f(20)$
を計算するには、まず副問題$f(19)$ と $f(18)$を計算し、次に$f(19)$を計算するために、副問題$f(18)$と$f(17)$など。 最後に、$f(1)$ または$f(2)$が検出された場合、結果は既知であり、結果を直接返すことができ、再帰木は下向きに成長しなくなる。
再帰アルゴリズムの時間計算量を計算する方法は, 副問題の数を掛ける副問題の解決に必要な時間である。
副問題の数は、即ち再帰木内のノードの総数。 明らかに、二分木ノードの総数は指数関数的であるため、副問題の数は$O(2^{n})$である。副問題を解く時間は、このアルゴリズムではループがなく、$f(n-1)+ f(n-2)$の加算のみで、時間は$O(1)$である。したがって、このアルゴリズムの時間計算量は$O(2^{n})$、指数関数!!
再帰木を観察すると、アルゴリズムの非効率的になる原因が明らかにする。$f(18)$が2回計算されるなど、繰り返し計算がたくさんあり、$f(18)$をルート(root)とする再帰木が巨大であることがわかるが 、そしてそれを再び数えることは膨大な時間を費やす。 さらに、繰り返し計算されるのは$f(18)$だけではない。この原因で、このアルゴリズムは非常に非効率的である。
これは、動的プログラミング問題の最初の性質であり、サブ問題の重複である。 以下では、この問題の解決を試む。
1.2 メモ化再帰
時間のかかる理由は繰り返し計算であるため、「メモ」を作成して、サブ問題の答えは、「メモ」に記録してから返す。 サブ問題にあったら、まず「メモ」に確認して、この問題が以前に解決されている場合は、答えを直接使用して、計算に時間を費やす必要はない。通常、このメモには配列が使用されているが、連想配列も使用できる。
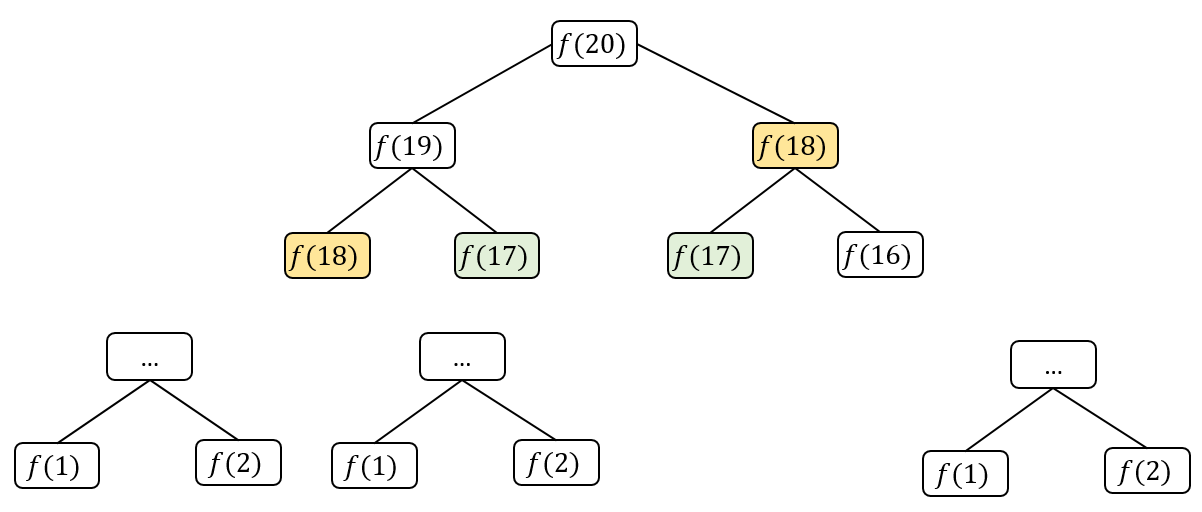
ここで、再帰木を描くと、「メモ」の機能が正確にわかる
実際、「メモ」を使う再帰アルゴリズムは、膨大な冗長性を持つ再帰木を「プルーニング」することで冗長性のない再帰グラフに変換し、サブプロブレム(再帰木のノード)の数を大幅に減らす。
明らかに、副問題の数はノードの数$n$である。副問題を解く時間は、このアルゴリズムではループがなく、時間は$O(1)$である。したがって、このアルゴリズムの時間計算量は$O(n)$であり、一般の再帰と比べ、雲泥の差である!
def fibonacci(n, memo={0:0, 1:1}):
if len(memo) <= n:
memo[n] = fibonacci(n - 1) + fibonacci(n - 2)
return memo[n]
これまでのところ、メモ化再帰法の効率は、動的計画法と同じである。 実際、この方法は動的計画法とほとんど同じですが、この方法は「トップダウン」と呼ばれ、動的計画法は「ボトムアップ」と呼ばれる。
「トップダウン」とは、 上で描いた再帰木は、すべて$f(20)$などのより大きな元問題から描画され、$f(1)$および$f(2)$まで徐々に分解して、分解できない最小問題に達して、レイヤーごとに解答に戻ることを「トップダウン」という。
「ボトムアップ」とは、下から、最も単純で最小問題$f(1)$および$f(2)$から始め、$f(20)$に到達するまで押し上げる。これが動的計画法の考え方である。 これが、動的計画法が、再帰から逸脱する理由であり、計算はループ反復によって行われる。
1.3 ボトムアップ法
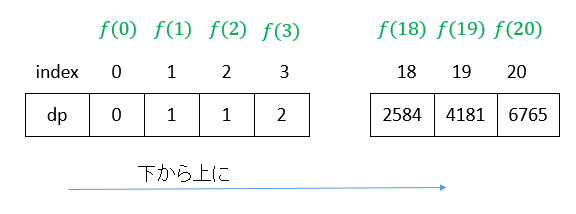
前のステップの「メモ」のヒントによって、この「メモ」をDPテーブルと呼ばれる。このテーブルを利用して、「ボトムアップ」計算する。
def fibonacci(n):
dp ={0:0, 1:1}
for i in range(2,n+1):
dp[i]=dp[i-1]+dp[i-2]
return dp[n]
絵を描いたら、理解しやすくなる。このDPテーブルは前の「プルーニング」後の結果に特に似ていることがわかるが、それはその逆にすぎない。 実際、メモ化再帰解法の「メモ」は最終的に完成したら、このDPテーブルと一致するために、2つの解法は実際には類似しており、ほとんどの場合、効率は基本的に同じである。
ここでは、「状態遷移方程式」という用語が派生している。これは、実際には問題の構造を説明する数学的形式である。
f(x)=\left\{\begin{matrix}
0\; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \;\;\; \; \; \;\;\;\;\;\;\; \; \; n=0\\
1\; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \;\;\; \; \;\;\; \;\;\;\;\;\;\; \;n=1\\
f(n-1)+f(n-2),\;n>1
\end{matrix}\right.
見ればわかるはず、状態遷移方程式、実は高校数学の漸化式に過ぎない
上記の解法のすべての演算、たとえば、$f(n-1)+f(n-2)$、$dp [i] = dp [i-1] + dp [i-2]$、および メモやDPテーブルの初期化操作は、「状態遷移方程式」を中心とする。 問題解決の核となる「状態遷移方程式」の重要性が挙げられていることがわかる。 実際には、状態遷移方程式が一般の再帰を直接に表していることはわかる
この例の最後に、コードを最適化する。フィボナッチ数列の状態遷移方程式によれば、現在の状態は前の2つの状態にのみ関連している。実際、すべての状態を格納するために、長いDPテーブルは必要ない。 したがって、さらに最適化して、空間計算量(Space Complexity)を$O(1)$に減らすことができる
def fibonacci(n):
assert isinstance(n, int), "n must be integer type!"
if n >= 2:
prev ,curr = 0, 1
for _ in range(2,n+1):
prev, curr = curr, prev+curr
return curr
elif n == 1:
return 1
elif n == 0:
return 0
else:
return None
2 お釣り問題
トピック:k種額面のコインを与える、額面はc1、c2 ... ck、各コインの数は無制限である。次に、合計金額を与え、この金額を構成するために少なくともいくつかのコインを尋ねる。 作成できない場合、アルゴリズムは-1を返す
たとえば、k = 3、額面値は1、2、5であり、合計金額= 11。 少なくとも3枚のコインが必要、つまり、11 = 5 + 5 + 1。
コンピュータはこの問題をどのように解決すべきだか? 明らかに、それは、すべての可能なコインの組合方法を列挙し、次に必要なコインの最小数を探すことである。
まず、この問題は「部分構造最適化」を持つため、動的計画法の問題である。 「部分構造最適化」を満たすためには、部分問題は互いに独立している必要がある。つまり、部分問題はお互いに影響を与えないことである。
なぜ、この問題は、部分構造最適化に満たすと言えるか。
例えば、合計金額 $amount = 11$(元問題)のとき、最小数のコインを見つけたい。もし、この時、金額 $amount = 10$ を満たす最小数のコイン(サブ問題)がわかっていれば、サブ問題の回答に1を加算すればよい(額面値が1のコインを選択する)だけで済む。コインの数に制限はなく、サブ質問間に相互に影響を与えなく、相互に独立している。
2.1 一般の再帰
これが動的計画法問題であることを知ったので、まず状態遷移方程式を正しく書く
最初に「状態」を決める。これは、元問題とサブ問題で変化する変数である。 コインの数は無制限なので、状態は目標金額だけとなる。
次に、dp関数を定義する。現在の合計金額は$n$であり、金額を構成するには少なくとも$dp(n)$個コインが必要である。
次に、「選択」を最適化する。つまり、各状態について、どのような選択を行えば、現在の状態を最適化する。 この問題には、コインを選択し、現在の目標金額に達成するコイン数を最小になる。
# 擬似コード
def coinChange(coins: List[int], amount: int):
# 定義:目標金額 n,少なくともdp(n)個コイン
def dp(n):
# 選択,最小コイン数の結果を選ぶ
for coin in coins:
res = min(res, 1 + dp(n - coin))
return res
# 元問題は dp(amount)
return dp(amount)
**最後,base caseを明確する。明らかに、この問題では、目標金額が0の時、必要コイン数は0であり、目標金額が小なり0の時、解はない、-1を返す
def coinChange(coins: list, amount: int):
def dp(n):
# base case
if n == 0: return 0
if n < 0: return -1
# 求最小值,所以初始化为正无穷
res = float('INF')
for coin in coins:
subproblem = dp(n - coin)
# 子问题无解,跳过
if subproblem == -1: continue
res = min(res, 1 + subproblem)
return res if res != float('INF') else -1
return dp(amount)
これまでのところ、状態遷移方程式は完成した。上記のアルゴリズムはすでに一般の再帰法である。上記のコードの数学的形式は、すなわち状態遷移方程式は
f(x)=\left\{\begin{matrix}
0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;n=0\\
-1,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; ほか\\
min \left \{ dp(n-coin)+1 | coin\in coins \right \}, n>1
\end{matrix}\right.
これまでのところ、この問題は実際に解決されたが、「重複サブ問題」を処理する必要があります。例えば、amount = 11、coins = {1,2,5}の場合に再帰木を描画すると
時間計算量の分析:サブ問題総数x各サブ問題計算時間。
副問題の総数は、再帰ツリー内のノードの数です。これはわかりにくいが、$O(n^k)$である。 各部分問題には、forループが含まれているため、複雑度が$O(k)$である。 したがって、合計時間の複雑さは$O(kn^k)$、指数関数である。
2.2 メモ化再帰
少し改修したら、メモ化再帰に書き換えることができる。
def coinChange(coins: list, amount: int) ->int:
# メモ
memo = dict()
def dp(n):
# 重複計算を防ぐ、まずメモの記録を探す
if n in memo: return memo[n]
if n == 0: return 0
if n < 0: return -1
res = float('INF')
for coin in coins:
subproblem = dp(n - coin)
if subproblem == -1: continue
res = min(res, 1 + subproblem)
# メモに記入
memo[n] = res if res != float('INF') else -1
return memo[n]
return dp(amount)
明らかに、メモ化によって、サブ問題の数は大幅に減らされる、サブ問題数は総金額nに超えない、つまりサブ問題の数は$O(n)$である。 サブ問題を処理する時間は変更されず、まだ$O(k)$なので、合計時間の複雑さは$O(kn)$である。
2.3 ボトムアップ法
もちろん、下から上にdpテーブルを使用して、重複サブ問題を処理することもできる。
def coinChange(coins:list, amount: int) -> int:
dp = [float('inf')] * (amount + 1)
dp[0] = 0
for coin in coins:
for x in range(coin, amount + 1):
dp[x] = min(dp[x], dp[x - coin] + 1)
return dp[amount] if dp[amount] != float('inf') else -1
3 最後のまとめ
最初のフィボナッチ数列問題は、「メモ」または「dpテーブル」を使用して、再帰木を最適化する方法を説明した。これら2つの方法は基本的に同じで、トップダウンとボトムアップの違いだけだ
2番目のお釣り問題は、「状態遷移方程式」を効率的に決定する方法を示した。状態遷移方程式が得たら、残りは再帰木を最適化し、重複問題を処理することである。
実際、コンピュータは、問題を解決するための巧妙方法がない、唯一の解決策はすべての可能性を徹底的に列挙することである。アルゴリズムは、まず「どうやって列挙」を考え、そして「どうやって巧妙に列挙」を実現できるだけだ。
状態遷移方程式を先に書くことは、「どうやって列挙」の問題を解決することである。
メモとDPデーブルは「どうやって巧妙に列挙」を実現する。空間計算量を増やして時間計算量を減らすことは、唯一無二の方法である。