はじめに
AI.RL.LYsのtyoshitakeです。
今回はガウス過程からのサンプリングの実装についての記事を書きました。
ガウス過程について
ガウス過程とは
通常ある変数$x$がある確率分布$D$に従う、つまり
x \sim D
のとき、$x$は分布$D$からランダムに生成されます。
ガウス過程の場合、N個の入力$\{x_1, x_2, ..., x_N\}$に対する出力$\{y_1, y_2, ..., y_N\}$の対応関係を関数$f$とすると関数fは多変量ガウス分布に従ってランダムに生成されます。
f \sim N(\mu, \Sigma)
ここで$\mu$は多変量ガウス分布の平均ベクトル、$\Sigma$は共分散行列になります。
ガウス過程の導出
以下では入力が1次元の場合(上の例で$x_i$がスカラの場合)のガウス過程の導出を見ていきます。
関数を行列表現
入力値$x$に対する関数は無数に考えられますが、ここでは特徴ベクトル
\boldsymbol{\phi}(x) = (\phi_0(x), \phi_1(x), ..., \phi_M(x))^T
を用いて以下のように表現するとします。
f(x) = \sum_{m = 1}^M w_m\phi_m(x)
ここで例えば
\phi_i(x) = x^i
とすると、$f(x)$は$x$の0次からM-1次までの線形和として表されます。
次に1次元の入力$\{x_1, x_2, ..., x_N\}$に対する出力$\{y_1, y_2, ..., y_N\}$を行列で表現すると以下のようになります。
\left(
\begin{matrix}
y_1 \\
y_2 \\
\vdots \\
y_N
\end{matrix}
\right)
=
\left(
\begin{matrix}
\phi_1(x_1) & \phi_2(x_1) & \dots & \phi_M(x_1) \\
\phi_1(x_2) & \phi_2(x_2) & \dots & \phi_M(x_2) \\
\vdots & \vdots & \vdots & \vdots \\
\phi_1(x_N) & \phi_2(x_N) & \dots & \phi_M(x_N)
\end{matrix}
\right)
\left(
\begin{matrix}
w_1 \\
w_2 \\
\vdots \\
w_M \\
\end{matrix}
\right)
または
\boldsymbol{y} = \Phi\boldsymbol{w} \\
$\boldsymbol{y}$はN次元ベクトル、$\Phi$はN行M列の行列、$\boldsymbol{w}$はM次元ベクトルです。
確率モデル化
係数ベクトル$\boldsymbol{w}$の各成分が平均0、分散$\lambda^2$のガウス分布からそれぞれ独立に確率的に生成されるとし、以下のM次元多変量ベクトルに従うとします。
\boldsymbol{w} \sim N(\boldsymbol{0}, \lambda^2I)
一般に多変量ガウス分布に従う確率変数に対し線形変換後の値も多変量ガウス分布に従うので1、$\boldsymbol{y} = \Phi\boldsymbol{w}$の関係から$\boldsymbol{y}$も多変量ガウス分布に従います。
また、$\boldsymbol{y}$が従う多変量ガウス分布の平均ベクトルと共分散行列はそれぞれ以下のようになります1。
平均ベクトル: \boldsymbol{0} \\
共分散行列: \lambda^2\Phi\Phi^T
したがって、
\boldsymbol{y} \sim N(\boldsymbol{0}, \lambda^2\Phi\Phi^T)
上では特徴ベクトル$\boldsymbol{\phi}$の次元をMとして計算しましたが、$M\to\infty$として特徴ベクトルを無限次元に拡張することができます(重み$w$の次元も無限になりますが、出力$\boldsymbol{y}$の分布の導出時に平均化してしまっているので問題なく扱えます)。
カーネル関数
$\boldsymbol{y}$の分布の共分散行列 $\lambda^2\Phi\Phi^T$ の$(i, j)$成分を取り出すと
(\lambda^2\Phi\Phi^T)_{ij} = \lambda^2\boldsymbol{\phi}(x_i)^T\boldsymbol{\phi}(x_j)
となり、共分散行列の$(i, j)$成分は入力$x_i$、$x_j$ の特徴ベクトル $\boldsymbol{\phi}(x_i)$、$\boldsymbol{\phi}(x_j)$の内積の定数倍となっています。
このように特徴ベクトルの内積として表現される関数
k(x_i, x_j) = \boldsymbol{\phi}(x_i)^T\boldsymbol{\phi}(x_j)
をカーネル関数と呼びます。
カーネル関数は特徴ベクトルの内積となっているので、入力$x_i$, $x_j$の特徴ベクトルが似通っている度合いを表していると解釈できます。
カーネル関数の具体例として次のガウスカーネル
k(x, x') = exp(-\beta \|x - x'\|^2)
を考えます。
ガウスカーネルを式変形すると
\begin{align}
k(x, x') &= exp(-\beta \|x - x'\|^2) \\
&= exp\{-\beta(x^2 + x'^2 - 2xx')\} \\
&= exp(-\beta x^2) \cdot exp(-\beta x'^2) \cdot exp(2\beta xx') \\
&= exp(-\beta x^2) \cdot exp(-\beta x'^2) \cdot \sum_{n=0}^\infty \left[ \frac{1}{n!}(2\beta xx')^n \right] \\
&= exp(-\beta x^2) \cdot exp(-\beta x'^2) \cdot \sum_{n=0}^\infty \left[ \frac{1}{\sqrt{n!}}(\sqrt{2\beta}x)^n \right] \left[ \frac{1}{\sqrt{n!}}(\sqrt{2\beta}x^{\prime})^n \right]
\end{align}
したがって以下の関数
\phi_i(x) = exp(-\beta x^2) \cdot \frac{1}{\sqrt{(i - 1)!}}(\sqrt{2\beta}x)^{i - 1}
を用いて、無限次元の特徴ベクトル $\boldsymbol{\phi}(x) = (\phi_1(x), \phi_2(x), \dots )$ を定めるとガウスカーネルは特徴ベクトル$\boldsymbol{\phi}$の内積で与えられ、実際にカーネル関数としての性質を満たしていることがわかります。
出力$\boldsymbol{y}$の分布の共分散行列を求める際には特徴ベクトルの内積を計算する必要がありますが、特に特徴量ベクトルの次元が大きい場合には内積を直接計算するよりもカーネル関数を用いて計算するほうが計算量が大幅に少なく済みます2。このように計算量を削減する方法はカーネルトリックと呼ばれます。
まとめ
ガウス過程において、1次元入力$\{x_1, x_2, ..., x_N\}$に対する出力は以下の多変量ガウス分布によってランダムに生成されます。
\boldsymbol{y} \sim N(\boldsymbol{0}, K) \\
ここで多変量ガウス分布の共分散行列$K$の$(i, j)$成分はカーネル関数$k$と定数$\lambda$を用いて以下のように計算されます。
K_{ij} = \lambda k(x_i, x_j)
上で見たようにカーネル関数は特徴ベクトルの内積で表現できるので、入力$\{x_1, x_2, ..., x_N\}$中の値$x_i$、$x_j$の特徴ベクトルが似ているほど対応する出力$y_i$、$y_j$が高い相関を持ちます。
実装
ガウス過程を実装し、出力のサンプリングを行いました。
計算条件は以下です。
- ガウスカーネル(1次元入力)
- 指数カーネル(1次元入力)
- 周期カーネル(1次元入力)
- ガウスカーネル(2次元入力)
カーネル関数
計算に使用したカーネル関数は以下のようになります。
ガウスカーネル
k(x_1, x_2) = exp\left(-\frac{\|x_1 - x_2\|^2}{\theta} \right)
指数カーネル
k(x_1, x_2) = exp\left(-\frac{\|x_1 - x_2\|}{\theta} \right)
周期カーネル
k(x_1, x_2) = exp\left(\theta_1 cos\left(\frac{\|x_1 - x_2\|}{\theta_2}\right) \right)
コード
ガウス過程からサンプリングを行うコードは以下です。
上記の条件でサンプリングを実行しサンプリングした結果の作図を行い、画像ファイルとして出力しています。
実行環境は以下です。
- python 3.6
- numpy 1.17.0
- matplotlib 3.1.1
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
def gaussian_kernel(x1: np.array, x2: np.array, param: np.array) -> float:
""" ガウスカーネルを計算する。
k(x1, x2) = exp(-|x - x2|^2/param[0])
Args:
x1 (np.array) : 入力値1
x2 (np.array) : 入力値2
param (np.array): ガウスカーネルのパラメータ
Returns:
float: ガウスカーネルの値
"""
return np.exp(-np.linalg.norm(x1 - x2)**2 / param[0])
def exp_kernel(x1: np.array, x2: np.array, param: np.array) -> float:
""" 指数カーネルを計算する。
k(x1, x2) = exp(-|x - x2|/param[0])
Args:
x1 (np.array) : 入力値1
x2 (np.array) : 入力値2
param (np.array): 指数カーネルのパラメータ
Returns:
float: 指数カーネルの値
"""
return np.exp(-np.linalg.norm(x1 - x2) / param[0])
def periodic_kernel(x1: np.array, x2: np.array, param: np.array) -> float:
""" 周期カーネルを計算する。
k(x1, x2) = exp(param[0]*cos(|x - x2|/param[0]))
Args:
x1 (np.array) : 入力値1
x2 (np.array) : 入力値2
param (np.array): 周期カーネルのパラメータ
Returns:
float: 周期カーネルの値
"""
return np.exp(param[0]*np.cos(np.linalg.norm(x1 - x2) / param[1]))
def calc_kernel_matrix(x: np.array, kernel: 'function', kparam: np.array) -> np.array:
""" カーネル行列を計算して返す。
カーネル行列Kの(i, j)成分はkernel(x[i], x[j])
Args:
x (np.array) : 入力値
kernel (function) : カーネル関数
kparam (np.array) : カーネル関数のパラメータ
Returns:
np.array: カーネル行列
"""
# カーネル行列の初期化
mkernel = np.zeros((x.shape[0], x.shape[0]))
for i_row in range(x.shape[0]):
for i_col in range(i_row, x.shape[0]):
mkernel[i_row, i_col] = kernel(x[i_row], x[i_col], kparam)
mkernel[i_col, i_row] = mkernel[i_row, i_col]
return mkernel
def gp_sampling(x: np.array, lm: float, mean: np.array, kernel: 'function',
kparam: np.array) -> np.array:
""" ガウス過程からサンプルした結果を返す。
Args:
x (np.array) : 入力値
lm (float) : 共分散行列の定数λ
mean (np.array) : ガウス過程の平均ベクトル
kernel (function) : カーネル関数
kparam (np.array) : カーネル関数のパラメータ
Returns:
np.array: サンプルした値
"""
# カーネル行列の計算
mkernel = calc_kernel_matrix(x, kernel, kparam)
# 共分散行列の計算
K = lm**2 * np.dot(mkernel, mkernel.T)
# サンプリング
return np.random.multivariate_normal(mean, K)
if __name__ == "__main__":
# 乱数シードの固定
np.random.seed(2)
fig = plt.figure(figsize=(18, 15))
# ガウスカーネル-1次元入力
x = np.linspace(0, 10, 200, endpoint=False)
kparam_list = [np.array([0.25]), np.array([0.5]), np.array([2.5])]
y_list = []
for kparam in kparam_list: # サンプリング
y_list.append(np.array([gp_sampling(x, 1.0, np.zeros(len(x)), gaussian_kernel, kparam) for i in range(3)]))
for i_plot, ys in enumerate(y_list): # 作図
ax = fig.add_subplot(3, 3, 3*i_plot + 1)
for y in ys:
ax.plot(x, y)
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_title('Gaussian Kernel')
# 指数カーネル-1次元入力
x = np.linspace(0, 10, 200, endpoint=False)
kparam_list = [np.array([0.25]), np.array([0.5]), np.array([2.5])]
y_list = []
for kparam in kparam_list: # サンプリング
y_list.append(np.array([gp_sampling(x, 1.0, np.zeros(len(x)), exp_kernel, kparam) for i in range(3)]))
for i_plot, ys in enumerate(y_list): # 作図
ax = fig.add_subplot(3, 3, 3*i_plot + 2)
for y in ys:
ax.plot(x, y)
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_title('Exponential Kernel')
# 周期カーネル-1次元入力
x = np.linspace(0, 10, 200, endpoint=False)
kparam_list = [np.array([1.0, 0.25]), np.array([1.0, 0.5]), np.array([1.0, 2.5])]
y_list = []
for kparam in kparam_list: # サンプリング
y_list.append(np.array([gp_sampling(x, 0.01, np.zeros(len(x)), periodic_kernel, kparam) for i in range(3)]))
for i_plot, ys in enumerate(y_list): # 作図
ax = fig.add_subplot(3, 3, 3*i_plot + 3)
for y in ys:
ax.plot(x, y)
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_title('Periodic Kernel')
fig.tight_layout()
fig.savefig('result1.png')
# ガウスカーネル-2次元入力
x = np.linspace(0, 10, 100, endpoint=False)
y = np.linspace(0, 10, 100, endpoint=False)
xx, yy = np.meshgrid(x, y)
shape_input = xx.shape
xy = np.c_[xx.reshape(-1), yy.reshape(-1)] # 2次元ベクトルの入力
kparam = np.array([.50])
z = gp_sampling(xy, 1.0, np.zeros(len(xy)), gaussian_kernel, kparam).reshape(shape_input)
fig = plt.figure()
ax = Axes3D(fig)
surf = ax.plot_surface(xx, yy, z, cmap='CMRmap', linewidth=0)
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
ax.set_title('Gaussian Kernel')
fig.tight_layout()
fig.savefig('result2.png')
結果
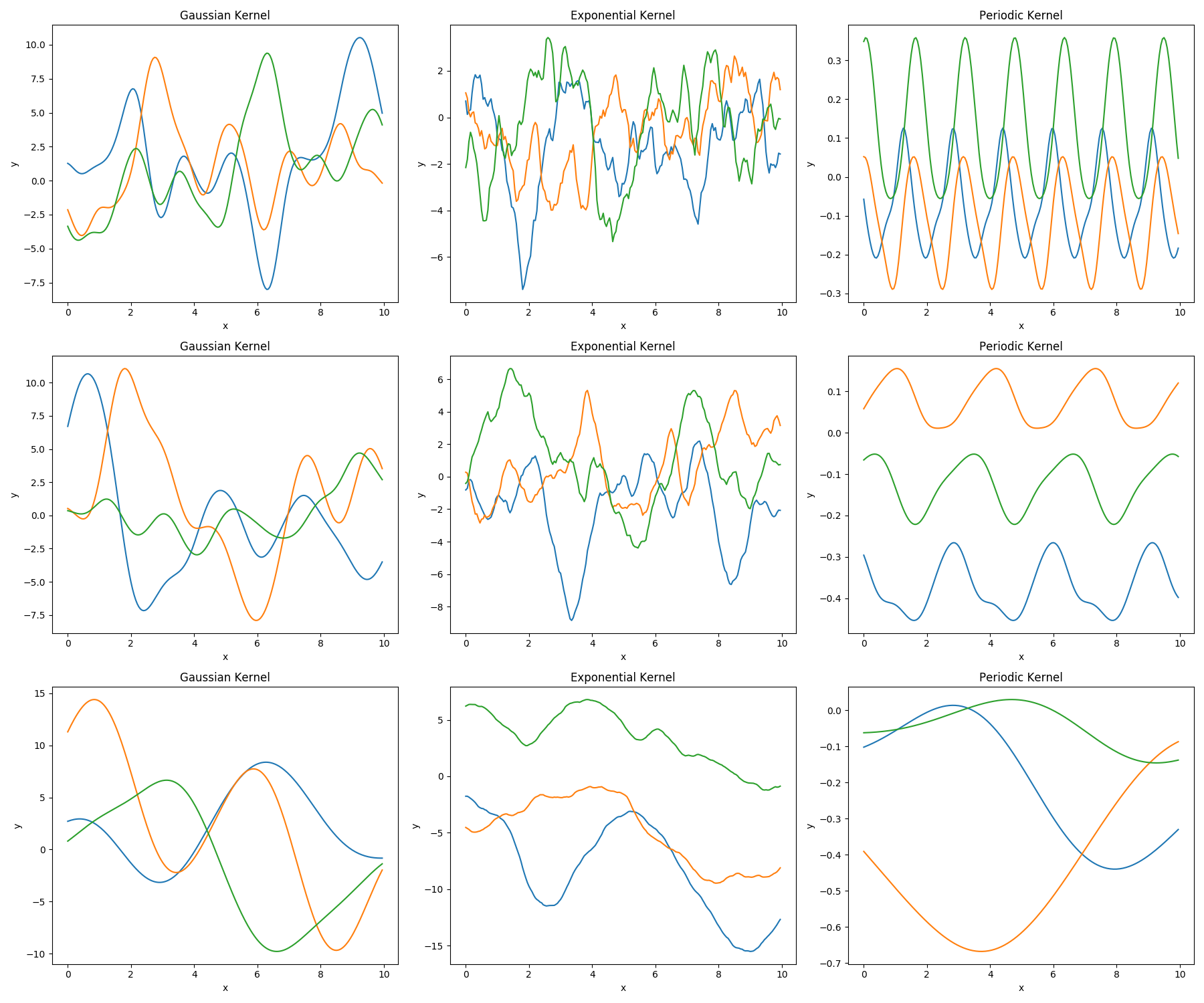
1次元入力に対しガウス過程のサンプリングを行った結果は下図のようになります。
左側の列からガウスカーネル、指数カーネル、周期カーネルを用いた結果に対応しており、各行の図はカーネル関数の入力データ間距離をスケールするパラメータを0.25, 0.5, 2.5としてサンプリングを行った結果です。各条件で3回サンプリングした結果を図示しています。
図を見るといずれの条件も入力に対する出力は隣接入力点の出力に近い(相関がある)値をとっていることがわかります。
また、カーネル関数のパラメータの値を大きくするにつれて図の曲線の振動周期が長くなっていることがわかります。これはパラメータを大きくすることで入力データ点間距離に対するカーネル関数値の値(すなわち、特徴ベクトルの類似度)がより大きくなり、離れた点との相関が強くなるためです。
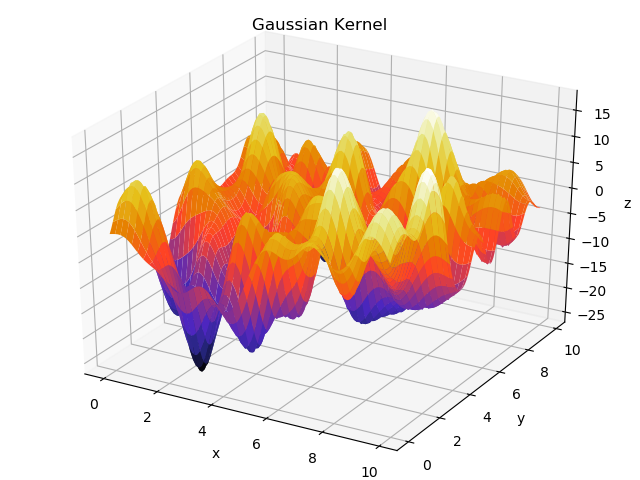
また、2次元入力に対しガウスカーネルを用いたガウス過程からサンプリングした結果は下図のようになります。
注意点
上のコードでは2次元入力のケースとしてサイズが10000のベクトルをサンプリングしており、計算に多少時間がかかります(i7-7660Uで数分程度)。
サンプリングに用いている関数(numpy.random.multivariate_normal)のアルゴリズムは計算量が $O(N^3)$ となっているので3、入力データサイズを増やす場合は計算時間に気をつける必要があります。
参考
- ガウス過程と機械学習
https://www.amazon.co.jp/dp/4061529269 - はじめてのパターン認識
https://www.amazon.co.jp/dp/4627849710
-
http://www.cs.columbia.edu/~liulp/pdf/linear_normal_dist.pdf 一般に多変量ガウス分布に従う変数 $\boldsymbol{x}$ ($\boldsymbol{x} \sim N(\mu_x, \Sigma_x)$)に対して線形変換($\boldsymbol{y} = A\boldsymbol{x}$)を行うと、変換後の変数 $\boldsymbol{y}$ も多変量ガウス分布に従う ($\boldsymbol{y} \sim N(\mu_y, \Sigma_y)$)。ここで $\mu_y=A\mu_x$, $\Sigma_y = A\Sigma_x A^T$ が成り立つ。 ↩ ↩2
-
一般に入力は多次元d。特徴ベクトルの次元をMとするとカーネルトリックを用いることでM次元データの計算をd次元データの計算に置き換えることができる。 d << Mの場合、計算量を大幅に削減できる。 ↩
-
https://stackoverflow.com/questions/40100340/numpy-multivariate-normal-bug-when-dimension-too-high ↩