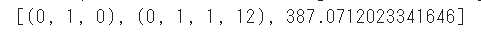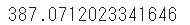初心者による株価予測

Posted at 2024-01-12

このブログはAidemy Premiumのカリキュラムの一環で、受講修了条件を満たすために公開しています

はじめに

Aidemy premiumにて「データ分析講座6ヶ月コース」を受講しました。

Aidemy premiumを受講した理由は、pythonやデータ分析、機械学習を学びそれらを活用した仕事に就きたいと思ったのがきっかけでした。

概要

●　どんな人に読んでほしいか
　　プログラミングやデータ分析に興味がある方。
　　これからプログラミング学習を始めてみようと考えている方。

●　この記事に書く事、わかること
　　SARIMAモデルによる機械学習。

●　この記事で扱わないこと、注意点
　　株価予測を扱いますが、数字上だけのものです。本来なら株価
　　予測は様々な要素を考慮して行いますが、今回はそれらを内容
　　に含んでいません。

目的

●　SARIMAモデルを用いた時系列分析を行い、株価予測をする。今回はMicrosoft社の株価データを用います。
●　学習した内容のアウトプット。また、簡単でも良いのでまずは完成させてみることを第一にしています。

実行環境

●　python 3.10.12
●　Google Colaboratory (Google Calab)

Google Calab上でPythonのバージョンを調べる場合は下記のコードを記述することで確認できます。

バージョン確認コード

! python --version
Python 3.10.12

時系列分析、SARIMAモデルについて

時系列分析、SARIMAモデルについて簡単に説明します。

時系列分析とは

「時間の経過とともに変化するデータを用いて変動要因やパターンを見つけ出し、将来の値を予測する統計的な手法」です。

例えば、東京の毎時間の気温の記録、会社の毎月の売上高の記録などが時系列データといえます。

時系列分析は、その時系列データから会社の売上や商品の売上予測、さらに来店者の予測など、ビジネスにおいて非常に重要な分析技術となります。

時系列データにはトレンド、周期変動、不規則変動の3パターンがあります。

トレンド
データの長期的な傾向を意味します。時間の経過とともにデータの値が上昇または下降していたりする時系列データは「トレンドがある」といいます。

周期変動
時間の経過に伴ってデータの値が上昇と下降を繰り返します。特に1年間での周期変動を「季節変動」といいます。

不規則変動
時間の経過と関係なくデータの値が変動することをいいます。

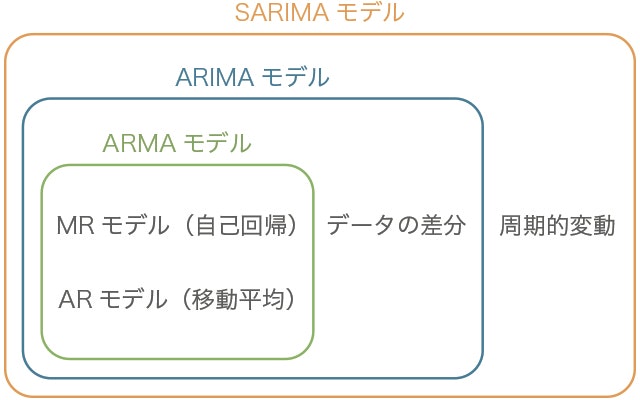
SARIMAモデル

SARIMAモデルを理解するために、まずその他のモデルについて説明します。

●　ARモデル (自己回帰モデル、AutoRegressive Model)
規則的に値が変化していくモデル。
過去の値から回帰的にある時点の値を推定します。
直前のp個の値を用いて次の値を予測するモデルをAR(p)と表現します。

●　MAモデル (移動平均モデル、Moving Average Model)
過去の誤差に影響されるモデル。
過去の誤差を考慮しながらデータの推移を予測します。
直前のq個の値の誤差の影響を受けるモデルをMA(q)と表現します。

●　ARMAモデル (自己回帰移動平均モデル、AutoRegressive Moving Average Model)
ARモデルとMAモデルを組み合わせたモデル。ARMA(p,q)と表せます。
ある時点の出力を、過去の出力と現在及び過去の入力に対する和で表現します。

●　ARIMAモデル (自己回帰和分移動平均モデル、AutoRegressive Integrated Moving Average Model)
ARMAモデルへ原系列を階差系列に変換し適応させたモデル。
非定常過程(データの平均や分散が時間に依存している過程)にも適応可能です。
d時点前との差分をとった場合のARMA(p,q)で構築したARIMAモデルをARIMA(p,d,q)と表します。

●　SARIMAモデル (季節変動自己回帰和分移動平均モデル、Seasonal AutoRegressive Integrated Moving Average Model)
ARIMAモデルを季節周期(s)を持つ時系列データにも拡張できるようにしたモデル。
(p,d,q)のパラメータに加えて(sp,sd,sq,s)のパラメータも持ちます。

株価データの取得

1.使用するライブラリをインポート

株価の取得はyahoo Financeから金融機関データを取得します。

import yfinance as yf
import pandas as pd
import numpy as pn
import matplotlib.pyplot as plt
import datetime
import itertools
import statsmodels.api as sm

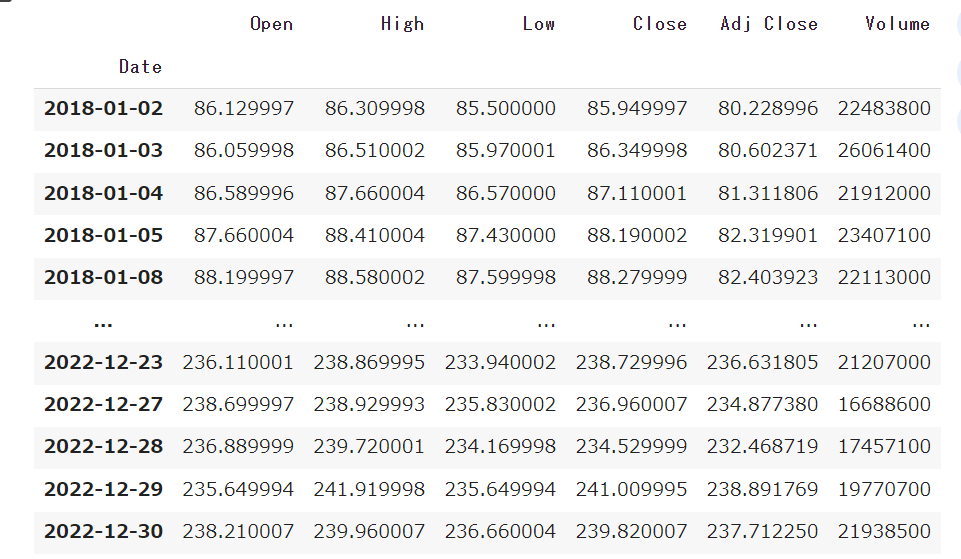
2.株価データの取得

Microsoft社の株価で、今回は2018年~2022年の5年間の期間で取得することにしました。

#ティッカーにMicrosoft社("MSFT")を指定。
#変数dfに株価データを代入。start,endで期間を指定。
ticker = "MSFT"
df = yf.download(ticker, start="2018-01-01", end="2022-12-31", interval="1d")
df

interval(頻度)は日単位、週単位、月単位などを選択できます。
今回は"1d"(1日)としました。

続いて、欠損値の確認をしていきます。
欠損値の有無は下記のコードで確認することができます。

#欠損値の確認
df.isnull().sum()

欠損値はありませんでしたので、このままこのデータを使用していきたいと思います。

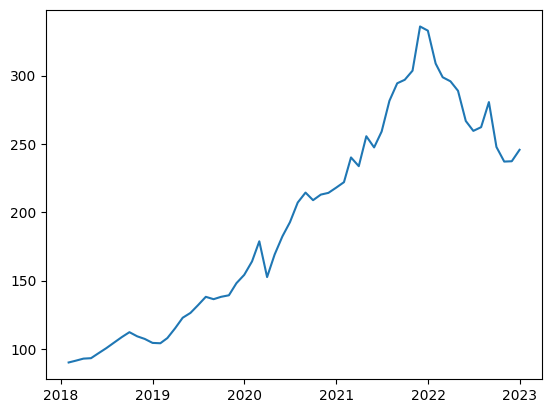
また、終値(Close)の値を使用するため、Closeを抽出しグラフにして可視化します。

#1ヶ月毎のデータに変更しシンプルにする
df = df.resample(rule = "M").mean()
#グラフにして可視化
plt.plot(df["Close"])
plt.show()

3.データの整理

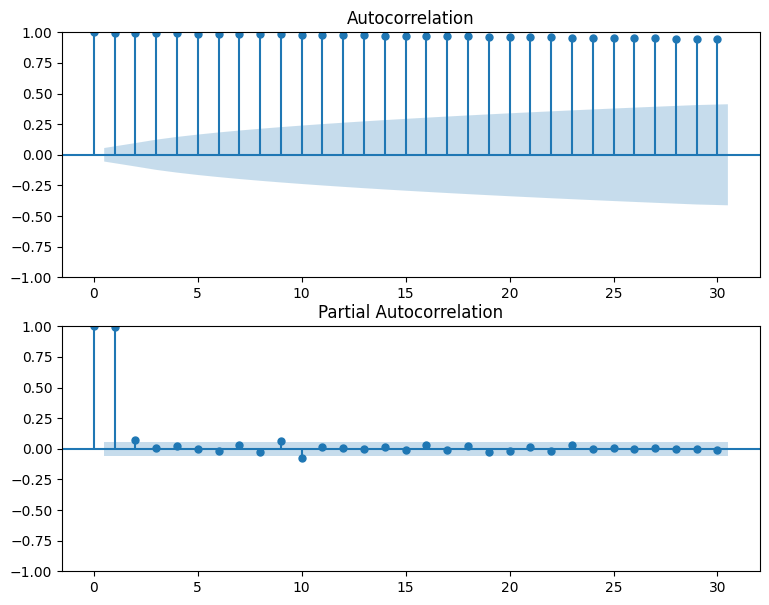
①　自己相関関数・偏自己相関
自己相関係数とは過去の値とどれだけ似ているかを表した値です。
偏自己相関とはある時点のデータが前のデータと相関がある場合にその影響を取り除いて相関を求めたものです。

自己相関関数と偏自己相関を可視化していきます。

#自己相関・偏自己相関の可視化
fig=plt.figure(figsize=(9, 7))

#自己相関係数のグラフを出力
ax1 = fig.add_subplot(211)
fig = sm.graphics.tsa.plot_acf(df["Close"], lags=30, ax=ax1)

#偏自己相関係数のグラフを出力
ax2 = fig.add_subplot(212)
fig = sm.graphics.tsa.plot_pacf(df["Close"], lags=30, ax=ax2)

plt.show()

コレログラムからは周期性は見られないのが分かります。

②　データパターンの確認
データパターンの確認の前に定常性について説明します。

時系列分析において重要な概念が「定常性」です。定常性とは、時間に依らず時系列データの確率分布が変化しないという確率過程の性質を表し、そのような確率過程を定常過程と呼びます。
言い換えると、時間の経過によらず一定の値を軸に同程度の幅で振れて変化すると言えます。

時系列データにおいて、定常性のないデータを分析した結果全く意味のない相関(Aが上がればBも上がる、もしくは下がるという関係)を検出してしまう可能性があります。
時系列データとは時間の経過に沿って変化するデータなので、「時間の経過」という共通項目が無意味な関係を生んでしまいます。このような無意味な相関の事を疑似相関といいます。

このような時系列データの疑似相関を検出しないために、定常性のない時系列は定常性のある時系列にしてから分析を進める必要があります。

時系列データを変換する方法の一つに、季節調整があります。
StatsModelsのtsa.sesonal_decompose()を使用することで、トレンド・季節変動・残差(=原系列-トレンド-季節変動)に分けることが可能です。残差は定常性のある時系列データになります。

sm.tsa.seasonal_decompose(df["Close"], period=12).plot()
plt.show()

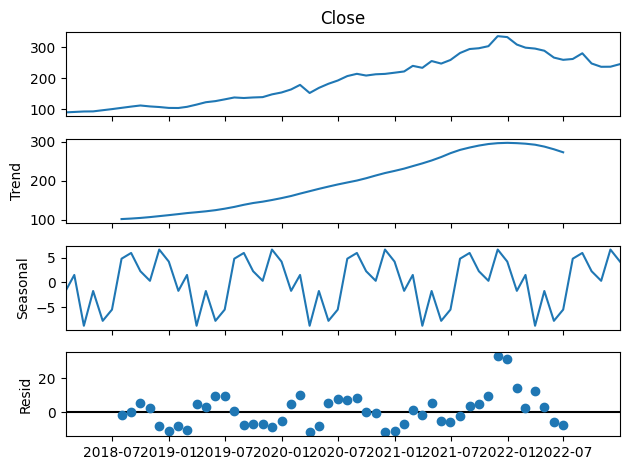
1番上が原系列、2番目がトレンド、3番目が季節性、4番目が残差です。
グラフより、トレンドと季節性があることが分かります。

株価予測の実践

①モデル・パラメータの決定
取得した株価データを整理しパターンの確認をしたところ、トレンド・季節性があることが分かりました。
よって、SARIMAモデルを使って分析を行いたいと思います。

pythonにはSARIMAモデルのパラメータ(p,d,q) (sp,sd,sq,s)を自動で最も適切にしてくれる機能はありません。
そのため、情報量基準(今回はBIC(ベイズ情報量基準))によってどの値が最も適切か調べるプログラムを書きます。
BICの場合はこの値が低ければ低いほどパラメータの値は適切であると理解してください。

def selectparameter(DATA,s):
    p = d = q = range(0, 2)
    pdq = list(itertools.product(p, d, q))
    seasonal_pdq = [(x[0], x[1], x[2], s) for x in list(itertools.product(p, d, q))]
    parameters = []
    BICs = np.array([])
    for param in pdq:
        for param_seasonal in seasonal_pdq:
            try:
                mod = sm.tsa.statespace.SARIMAX(DATA,
                                                order=param,
                                                seasonal_order=param_seasonal)
                results = mod.fit()
                parameters.append([param, param_seasonal, results.bic])
                BICs = np.append(BICs, results.bic)
            except:
                continue
    return parameters[np.argmin(BICs)]

selectparameter(df["Close"],12)

②モデルの構築
最適なパラメータ(p,d,q),(sp,sd,sq,s)が分かったので、モデルを構築していきます。
モデルの構築にはsm.tsa.statespace.SARIMAX(DATA,order=(p,d,q),seasonal_order=(sp, sd, sq, s)).fit()を用います。

#モデルの構築
SARIMA_MSFT = sm.tsa.statespace.SARIMAX(df["Close"],order=(0, 1, 0),seasonal_order=(0, 1, 1, 12)).fit()

print(SARIMA_MSFT.bic)

③モデルの予測データの取得・可視化
モデルの予測データを得ます。
モデル名.predict("予測開始時","予測終了時")とすると予測データが得ることができます。
また、得られたデータを可視化します。

#predに予測データを代入
pred = SARIMA_MSFT.predict('2021-1', '2023-12')

#predと元の時系列データを可視化
#予測データは赤色で表示
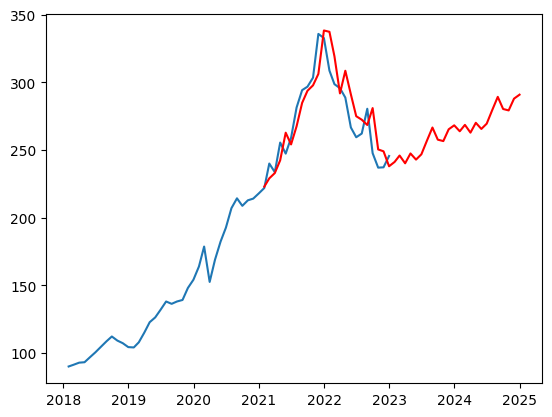
plt.plot(df["Close"])
plt.plot(pred, "r")
plt.show()

予測結果は以下のようになりました。

元のデータと比較すると、予測データに若干の差異がありますが概ね合致しています。
また、2023年以降の株価は緩やかではありますが、上昇していくと予測しています。このペースで行くと、2027年くらいには2022年と同程度の株価になっているのではないでしょうか。(あくまで予測です。)

今後の課題

今回の株価予測はSARIMAモデルを用いた時系列分析を行いましたが、方法は他にもあるので、様々な分析方法を学習して使いこなせるようにしていきたいです。

終わりに

受講始めは、分からないことばかりでしたが、実際にコードを書いてみてエラーなく出力されたときの喜びが学習のモチベーションになっていました。
また、分からない部分やエラーが出た時は、その都度チューターの方達に質問ができるので、挫折することなく学習を進められました。
もちろん、このブログ作成にもお力添えいただいたおかげで完成させることができました。
Aidemy社にはとても感謝しています。

これからも学習を続けていき、さらにレベルアップしていきたいと思います。

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up