AutoCADのポリライン図形とは
- 線分と円弧で構成された、単一の図形。
- PLINE コマンドで作成することができる。
- 線分のみ、円弧のみのポリラインも作成することができる。
- ポリラインの始点と終点をつなげた、閉じたポリラインを作成できる。
ポリラインは各頂点の座標（2D点）と、”ふくらみ” と呼ばれる実数で定義されている。
ふくらみ（英語で bulge）とは
ふくらみが "$0.0$" の場合、そのポリラインの要素は線分を表している。
円弧の場合、その円弧の中心角を $\theta$ （ラジアン単位）とした場合、
$$bulge=\tan\left(\frac{\theta}{4}\right)$$
がポリラインのDXFデータ（Group Code : 42）に格納されている。
円弧が時計回りの場合は "$-$"、反時計回りの場合は "$+$" の値となっている。
DXFデータの例
このDXFデータを見ると、頂点2と頂点3の間の要素が円弧であることがわかる。
この円弧の中心角は $90$度 $\left(=\dfrac{\pi}{2}\right)$ なので、ふくらみの値は、
$$bulge=\tan\left(\frac{\pi/2}{4}\right)=\tan\left(\frac{\pi}{8}\right)\fallingdotseq0.414214$$
となっている。
また、この円弧は頂点2から頂点3に向かって、反時計回りとなっているので、正の数値となっている。
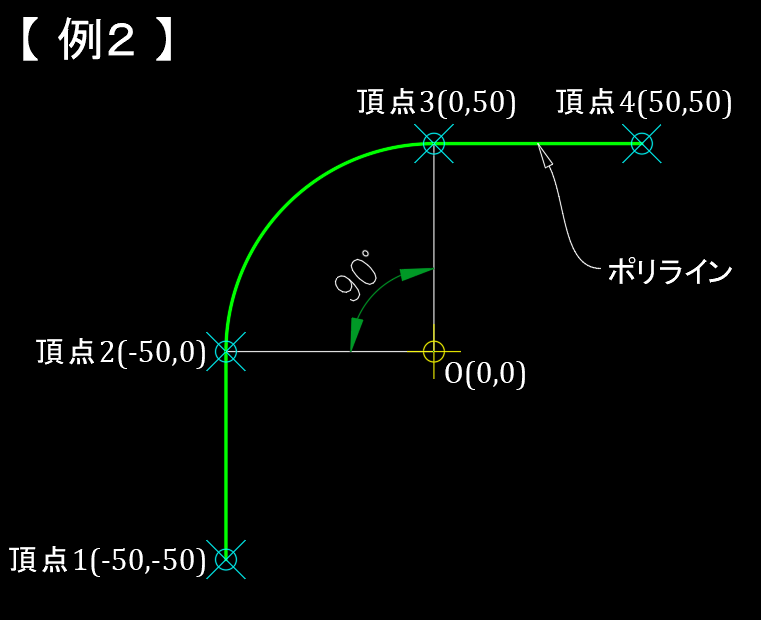
例２は例１の図形をY軸で反転した図形で、ふくらみは頂点2から頂点3に向かって、時計回りとなっているので、
$$bulge\fallingdotseq-0.414214$$
となっている。
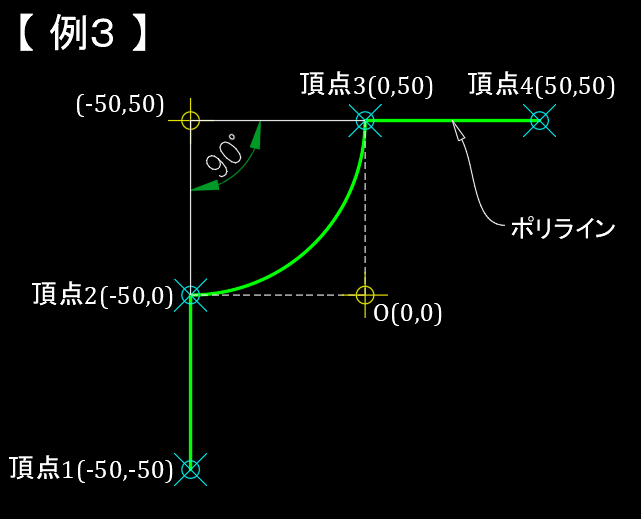
例３は例２と頂点の座標は同じで、ふくらみは頂点2から頂点3に向かって、反時計回りとなっているので、
$$bulge\fallingdotseq0.414214$$
となっている。
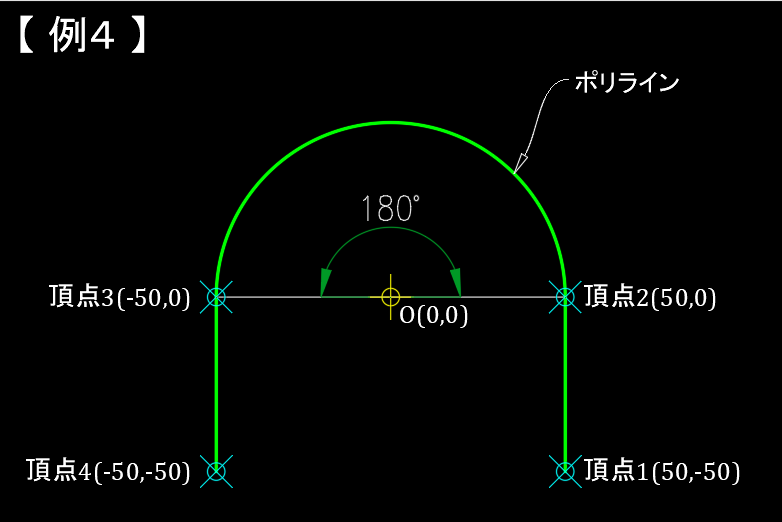
例４の円弧の中心角は $180$度 $(=\pi)$ なので、ふくらみの値は、
$$bulge=\tan\left(\frac{\pi}{4}\right)=1.0$$
となっている。
また、この円弧は頂点2から頂点3に向かって、反時計回りとなっているので、正の数値となっている。
頂点とふくらみ、円弧の計算
AutoCADの円弧は、中心、半径、開始角度と終了角度によって定義されている。
ポリラインの頂点とふくらみ情報から、円弧の定義に使用される数値を計算することができる。
逆に、円弧の定義情報から、ポリラインの頂点とふくらみを計算することもできる。
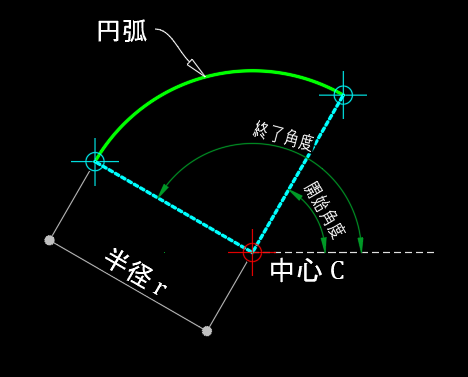
円弧の定義から頂点とふくらみを求める
円弧の中心の座標を $(x_0,y_0)$、半径を $r$、開始角度を $\alpha$、終了角度を $\beta$、とすると
点 $A$ の座標は
$$(x_0+r\cos\alpha , y_0+r\sin\alpha)$$
点 $B$ の座標は
$$(x_0+r\cos\beta , y_0+r\sin\beta)$$
中心角は、
$$\theta=\beta-\alpha$$
よってふくらみは
$$bulge=\tan\left(\frac{\beta-\alpha}{4}\right)$$
となる。
頂点とふくらみから円弧を求める
ふくらみの定義は、円弧の中心角を $\theta$ とした場合、$\tan\left(\dfrac{\theta}{4}\right)$で定義されている。
ふくらみ$(bulge)$ を $b$ とすると中心角は、
$$\theta=4\arctan(b)$$
となる。
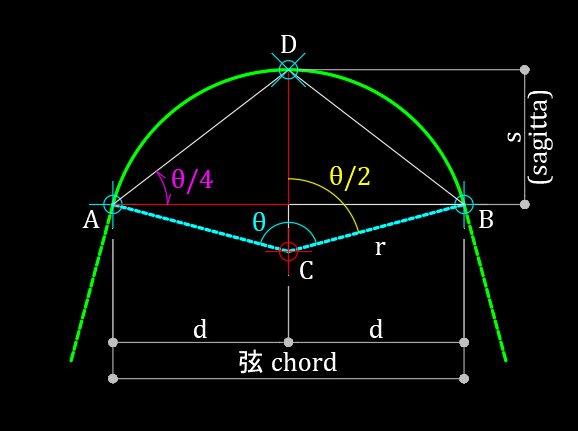
図のように円弧の始点$A$と終点$B$を結んだ弦と、始点$A$ と円弧の中点 $D$ を結んだ線分 $AD$が作る角、$\angle DAB$ の角度が $\dfrac{\theta}{4}$となっている。
ふくらみ $(bulge)$ の定義が $b=\tan\left(\dfrac{\theta}{4}\right)$ なので、
円弧の弦（線分$AB$）の半分の長さを $d$ としたとき、図の $s$ （$sagitta$ と呼ぶらしい）は、
$$s=bd$$
で求めることができる。
円弧の半径を $r$ とすると、三平方の定理より
$$r^2=d^2+(r-s)^2$$
が成り立つ。
この式を展開して整理すると、
$$r=\frac{s^2+d^2}{2s}$$
よって半径 $r$ は、
$$r=\frac{s^2+d^2}{2s}=\frac{d(b^2+1)}{2b}$$
で求めることができる。