単純な閉路

単純な閉路とは

与えられたN個の点をすべて通り、途中で交差せずに出発点に戻るような道を求める。
この道を単純な閉路(simple closed path)とよぶ。

計算の手順

1. 与えられた点の中で、yの値が最も小さい点を求めて基準点とする。（yが同じ場合はxが小さい方にする）
2. 各点と基準点を結んだ線分と、基準点から水平方向の向きに引いた直線とのなす角を計算する。
3. 2で求めた角度が小さい順に点を整列する。
4. 基準点を始点に整列した順に点を結ぶ

計算例

下図のような、点AからHまでの点の集合を考える。

1. yの値が最も小さい点Cを基準点とする。
2. 各点と点Cを結んだ線分と、点Cから水平方向の向きに引いた直線とのなす角を計算する。

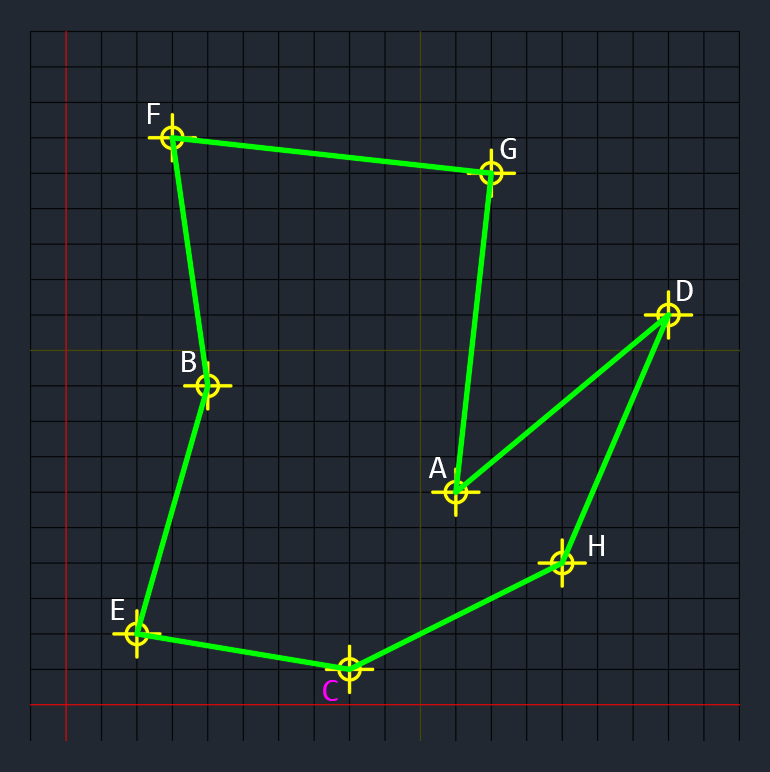3. 2で求めた角度が小さい順に点を整列する。上図によると、C → H → D → A → G → F → B → E の順となる 4. C → H → D → A → G → F → B → E → C の順に点を結ぶ 5. 完成

プログラム

( AutoLISP )
比較用の角度を計算する関数

(defun point:GetComparisonAngle (p q / ax ay dx dy theta)
	(setq dx (- (car q) (car p))
		  ax (abs dx)
		  dy (- (cadr q) (cadr p))
		  ay (abs dy)
	)
	(if (zerop (+ ax ay))
		(setq theta 0)
		(setq theta (/ (* dy 1.) (+ ax ay)))
	)
	(if (< dx 0)
		(setq theta (- 2 theta))
		(if (< dy 0)
			(setq theta (+ 4 theta))
		)
	)
	(* theta 90.)
)

単純な閉路となる順番に点を並べ替える

(defun point:GetSimpleClosedPath (points / basePoint)
	;; 基準点を取得(Y値が最小の点)
	(setq basePoint
			 (car
				 (vl-sort points
					 (function
						 (lambda (p q)
							 (if (= (cadr p) (cadr q))
								 (< (car p) (car q))
								 (< (cadr p) (cadr q))
							 )
						 )
					 )
				 )
			 )
	)
    ;; 基準点との角度を比較して点を並べ替える
	(vl-sort points
			 (function
				 (lambda (p q)
					 (<
						 (point:GetComparisonAngle basePoint p)
						 (point:GetComparisonAngle basePoint q)
					 )
				 )
			 )
	)
)

;; < Example >
(point:GetSimpleClosedPath '((11 6) (4 9) (8 1) (19 11) (2 2) (3 16) (12 15) (14 4)))
;; -> ((8 1) (14 4) (19 11) (11 6) (12 15) (3 16) (4 9) (2 2))