はじめに
ゲーム制作で簡単なアニメーションを実装する際にイージングが便利でよく使いますよね!
私もよく以下のページとにらめっこしてハマりそうなプリセットを使ったり
自分でイージング関数を実装したりしています。
さて、今回は高校数学でも習う対数関数「$logx$」を使ったちょっとしたイージングのチューニング小ネタを紹介します。
対数関数
対数について軽く復習しましょう。
ある数 $x$ を $b^p$ と表した際に、この$p$を「底$b$とする$x$の対数」と呼び
log_{b}x
と表しました。
なので、このような対数があった場合、以下のような数式も成り立ちました。
b^{log_bx}=x
冪関数
続いて冪関数についても軽く見ていきます。
(指数関数ではなく冪関数にしているのは、今回の話題においてこれが都合がいいからです)
x^a
さて、ここで注目したいのが
少なくとも実数の範囲では
- $x$ が $0$ のとき $a\neq0$ ならば、いかなる値だとしても $0^{a}$ は $0$ になります
- 同様に、$x$ が $1$ のとき $a$ がいかなる値だとしても $1^{a}$ は $1$ になります
つまり
冪関数は、$a\neq0$ ならば絶対に$(0, 0)$と$(1, 1)$を通ることが分かります。
任意な点を通る なめらかな曲線
ここで
x^{log_ab}
という関数を考えてみます。
$a$, $b$をそれぞれ
- $0 < a < 1$
- $0 < b < 1$
の範囲とした場合
この関数は、先ほどまで見てきた対数関数、冪関数の性質から
以下の三点をとおるなめらかな曲線であることがわかります。
※a,bが同じ値の場合、直線になる
- $(0, 0)$
- $(a, b)$ (任意の点)
- $(1, 1)$

イージング関数等と組み合わせる
先ほど考えた$x^{log_ab}$という関数。いったい何が嬉しかったのかという
イージング関数自体が
時間軸$t$において始点を$t=0$、終点を$t=1$とした場合
$0$~$1$の範囲での変化とみることができるので

この$t$に$x^{log_ab}$を適用することで、イージング関数を
任意の点を通るくらいにいい感じに歪ませることができます。
例1 イージング関数
例えば、上記のeaseInSineの例でいえば、
だいたい$t=0.6$の時に$0.4$くらいの値を通っていますが
もう少し早く$t=0.5$くらいの時には$0.4$くらいの値を通ってほしいと思ったとします。
それであれば$t$を$t^{log_{0.5}0.6}$にしてしまえばいいのです!
// easeInSine(t); を以下のように修正
easeInSine(pow(t, log(0.6, 0.5)));
※log(a, b)をbを底とした対数関数とする

例2 三角関数
sin関数なんかも歪ませちゃえます。
最大値に到達する時間をもう少し早めてみます。(※減少速度が下がることに注意)
// sin(t * PI); を以下のように修正
sin(pow(t, log(0.5, 0.4)) * PI);
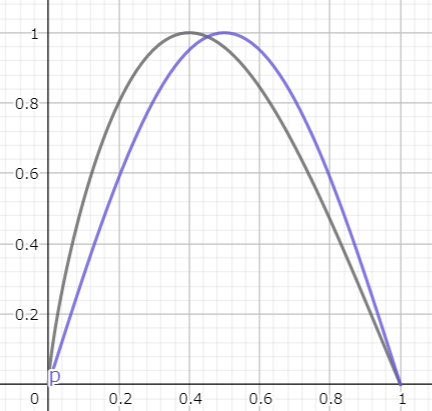
このように、対数関数と冪関数の関係を上手く活用した$x^{log_ab}$を挟むことで、任意の点$(a, b)$をとおるように、他の関数を歪ませることができます。
ゲーム制作では、細かい動きの調整をする機会が多いと思うので、似たようなイージングはあるのだけど、ちょっと理想のタイミングとずれてるなと思った時とかに、いい感じに歪ませることでそれっぽい動きができあがるかもしれません!
おまけ 底を指定する対数関数の実装
なお、プログラミング言語によっては、組み込みで用意されてるlog関数が底の指定ができないこともあると思います。(一般的には底はe?)
その場合は自分で底を指定する対数関数の実装が必要になりますが、
こちらは、高校数学でも習った以下の式により簡単に実装できます。
log_ax=\frac{log_bx}{log_ba}
// aを底とする対数関数
log(x) / log(a)
まとめ
- 対数関数と冪関数の関係を利用した$x^{log_ab}$は任意の点$(a, b)$を通るなめらかな曲線
※($0 < a,b < 1$) - イージング関数等に上記関数を適用することで任意の点をとおるように歪ませることができる
- アニメーション変化の細かいチューニングで活用できる