はじめに
高校数学で習う微分積分の知識をプログラミングで使える時があったりするので、その話
サンプルコードはC++とSiv3Dで書いています。
積分とは
数学科ではないので数学的な説明ははぶきますが、(まちがってるかもですが)
\int f(x)dx
って簡単に言うとあるxの範囲でのf(x)の和なんですね
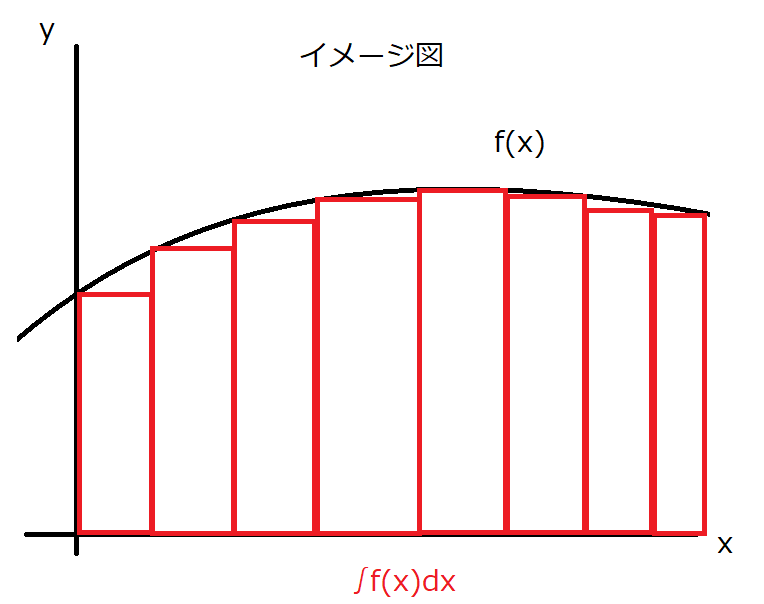
面積を求めるときに積分しましたよね?イメージ図では幅が大きいですが極限まで小さいと考えてもらえればわかりやすいかなと思います。
プログラミングで考えてみる
例えば二次関数
y=0.01x^2+100
にそって動かしたいとした時、普通に考えれば
# include <Siv3D.hpp>
void Main()
{
Graphics::SetBackground(Palette::White);
double x = 0;
double y = 0;
while (System::Update())
{
x += 0.5;
y = 0.01*x*x + 100;
Circle(x, y, 10).draw(Color(Palette::Red, 128));
}
}
で、できますが
微積の考えを利用すると
\frac{dy}{dx} =0.02x\\
y=\int \frac{dy}{dx} dx+100
と考えることもできます。
さて、先ほど積分は和であるといいました。
これはプログラミングでは、メインループで毎フレーム加算することで表現できます。
現在のフレーム数をtとした時
今回の例だと1フレーム事のxの増加量は0.5なので
x=0.5t
になります。
tフレーム目のyの値を知るには
\frac{dx}{dt} =0.5\\
x=\int \frac{dx}{dt} dt\\
\frac{dy}{dt} =0.02x*\frac{dx}{dt}\\
y=\int \frac{dy}{dt} dt+100
と考えることができます。
さきほどの例をこの考えで書き直してみましょう
# include <Siv3D.hpp>
void Main()
{
Graphics::SetBackground(Palette::White);
double x = 0;
double y = 100; //初期値100
while (System::Update())
{
double dxdt = 0.5;
x += dxdt;
y += 0.02*x*dxdt;
Circle(x, y, 10).draw(Color(Palette::Blue, 128));
}
}
積分の部分を毎フレーム加算にし、定数部分は初期値にすることで表現できます。
実際に比較する
紹介した二つの動きを実際に実行して比較してみてください!
ほぼ同じ動きになるはずです。
# include <Siv3D.hpp>
void Main()
{
Graphics::SetBackground(Palette::White);
double x = 0;
double y = 0;
double y2 = 100;
while (System::Update())
{
double dxdt = 0.5;
x += dxdt;
y = 0.01*x*x + 100;
y2 += 0.02*x*dxdt;
Circle(x, y,10).draw(Color(Palette::Red,128));
Circle(x, y2, 10).draw(Color(Palette::Blue, 128));
}
}
さらに微分してもOK
2回微分しても同じ考えで計算できます。
\frac{d^2y}{dt^2}=0.02(\frac{dx}{dt})^2\\
\frac{dy}{dt} =\int \frac{d^2y}{dt^2} dt\\
y=\int \frac{dy}{dt} dt+100
# include <Siv3D.hpp>
void Main()
{
Graphics::SetBackground(Palette::White);
double x = 0;
double y = 0;
double dydt=0;
double y3 = 100;
while (System::Update())
{
double dxdt = 0.5;
x += dxdt;
y = 0.01*x*x + 100;
dydt += 0.02*dxdt*dxdt;
y3 += dydt;
Circle(x, y,10).draw(Color(Palette::Red,128));
Circle(x, y3, 10).draw(Color(Palette::Lime, 128));
}
}
応用例
いろいろ話をしてきましたが、もう少しゲームっぽい話をしてみます。
アクションゲーム等でジャンプを放物線的にしたい時
僕は高校のころ、物理で
変位の微分=速度
速度の微分=加速度
と習いました。
y軸の加速度は重力のみと考えるとすると、
# include <Siv3D.hpp>
void Main()
{
Graphics::SetBackground(Palette::White);
double gravity = 0.3;//重力
double y = 0;
double vy = 0;
double ay = gravity;
while (System::Update())
{
vy += ay;//速度は加速度の積分
if (vy > 10)
vy = 10;
y += vy;//変位は速度の積分
if (y > 400)
y = 400;
if (Input::KeySpace.clicked)
vy = -10;
Circle(320, y, 40).draw(Palette::Red);
}
}
こんな感じで簡単に放物線的なジャンプが作れます。(これだけだと無限ジャンプになるが)
ちなみに、xに加速度をつけると慣性がつけれたりします。
三角関数的に動くやつ
sinの微分はcos
cosの微分は-sinでした
初期位置から100の幅でsin関数的に動くやつを考えてみます。
# include <Siv3D.hpp>
void Main()
{
Graphics::SetBackground(Palette::White);
double y = 240;//初期位置
while (System::Update())
{
auto t = static_cast<double>(System::FrameCount());
/*
y = 100 * Sin(t/10.0)+初期位置;で動く
*/
double vy = 100*Cos(t/10.0)/10.0;//dy/dt
y += vy;
Circle(320, y, 40).draw(Palette::Red);
}
}
この程度なら直接代入でもいい気もしますが、昔ゲームを作っていた時に
敵キャラごとに速度だけ変えて、どのキャラも座標に速度を足していくだけの設計にした時に使えたりしました。
その他
電磁気学とかでもコンデンサーとかで微積がでてきた記憶があるので、シミュレートできると面白そう。(ちなみに僕は電磁気学不可wなので何もわかりません)
まとめ
今回メインループで加算していくことを利用して、直接表現したい動きを微分した形に落とし込むことができました。
式を
\int f(x)dx+C
で表したとき
積分は毎フレーム加算
定数は初期値
で表現することができました。
ただ、実際のゲーム制作において、こういった方法か直接代入する方法どちらがいいのかは自分にもわかっていません。