Rのパッケージroplsでは、pca(principal component analysis:主成分分析)の他に、pls(Patial Least Squre Regression:部分最小二乗法回帰)、opls(orthogonal projections to latent structures:潜在構造に対する直交射影)、さらにそれらの判別分析であるpls-DA, opls-DAが使えます。
PLS回帰は目的変数と説明変数からなる行列データで、説明変数が観測数(サンプル数)よりも多い時、そして説明変数の値の間に相関があって多重共線性が存在する時に特に適しています。oplsはplsの進化版で、目的変数の予測軸とそれに対する直行軸で作成されるために、視認性に優れています。
生化学系のメタボロミクス分析に良く使われているそうです。
線形の多変量解析にはとても便利なので、Rのroplsパッケージを良く使っています。
まずは、パッケージroplsで提供されているデータセット"foods"で試してみましょう。foodsはヨーロッパ16ヶ国の20の食品の消費量の相対値のデータだそうです。
roplsはRの生化学向けライブラリサイトのBioconductorに掲載されています。
roplsのサイト
環境
windows10
R 3.6.1
ropls 1.16.0
roplsのインストール
以下はRのバージョンが3.6向けです。
if (!requireNamespace("BiocManager", quietly = TRUE))
install.packages("BiocManager")
BiocManager::install("ropls")
packageVersion("ropls") #インストールされたroplsのバージョンの確認
Rの旧バージョンでのroplsのインストール方法は以下のリンクを参照ください。
Release versions
パッケージroplsとデータセットfoodsの読み込み
library(ropls)
foods <- data(foods)
str(foods) #データfoodsの確認
rownames(foods) <- foods$country #1列目のcountryをrownamesに指定
foods <- foods[, -1] #1列目を削除
num.col <- ncol(foods) #列数を代入
num.row <- nrow(foods) #行数を代入
データセットfoodsにはヨーロッパの16か国における20品目の食品の消費量の相対値が記載されています。 1列目が国名になっているので、これをrownames(行名)に指定して、1列目を削除しておきます。
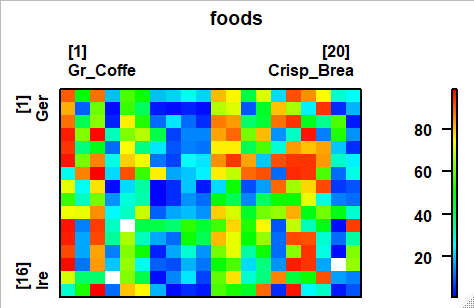
データ行列をヒートマップ風に視覚化
新たに追加されている関数imageFを使います。
imageF(foods)
関数oplsで、pca, pls, opls が選択的に実行できます。
pca 主成分分析
foods.pca <- opls(x = foods, y = NULL, predI = NA, scaleC = "standard")
引数x = foodsで説明変数を指定、y = NULL(デフォルト設定、省略可)で目的変数を指定しないので、pcaを実行します。
predI = NA(デフォルト設定、省略可)で主成分数を自動で決定します。
scaleC = "standard"(デフォルト設定、省略可)でデータの標準化(各説明変数の平均値を0、標準偏差を1として)を指定します。
他に、
"none": no centering nor scaling、
"center": mean-centering only,
"pareto": mean-centering and pareto scaling、
が選択できます。
以下の出力結果がコンソール画面に表示されます。

1行目に分析の種類、2行目にサンプル数と説明変数の数、3行目にデータの標準化について、4行目の"3 (1%) NAS "とは欠損値が3(全データの1%)あるという意味です。
5行目以降に、2つの主成分の寄与率の合計がR2X(cum) = 0.502,
主成分数が pre =2 が表形式で表示されています。
自動的に主成分数が2になっていますが、predI = で主成分数は最大10まで設定できます。
自動設定は以下のルールと記載されています。
the variance is less than the mean variance of all components
(note that this rule requires all components to be computed and can be quite time-consuming for large datasets)
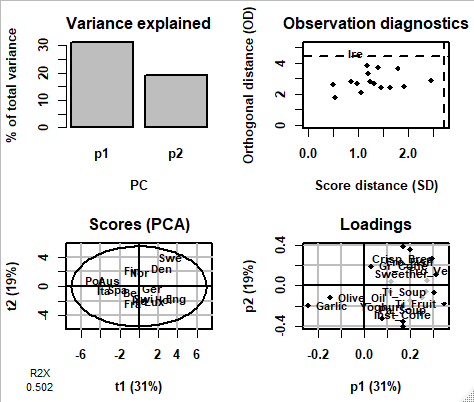
左上図で各主成分の寄与率が示されています。右上図で外れ値のサンプルに確認を行います。横軸のScore distance(SD)で点線より右がわにあるサンプルは外れ値として、削除するか検討候補になります。
左下図はスコアプロット、右下図はローディングプロットになります。
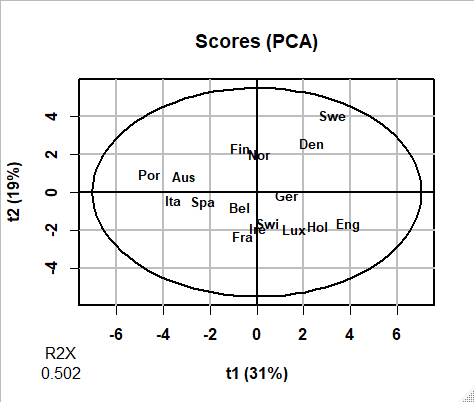
あらためて、スコアプロットとローディングプロットを表示させます。
plot(foods.pca, typeVc="x-score", parCexN = 0.8)
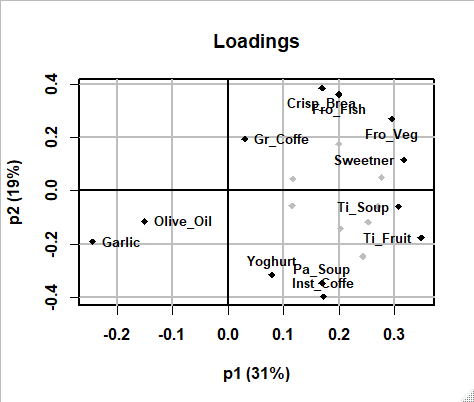
plot(foods.pca, typeVc="x-loading", parCexN = 0.8)
引数 typeVc = でプロットのタイプを指定します。
parCexN = でプロットのテキストの大きさを相対値で指定できます。
スコアプットとローディングプロットから各主成分の特徴を解釈します。
ローディングプログラムロットは各主成分の両端から3つの説明変数(特徴量)の名前を表示してくれます。
第一成分(横軸)は正方向にTi-Fruit(Tin Fruit)、Sweetner、Fro_Veg(Frozen Vegetables)の消費が高く、Galic、Olive_Oilの消費が少ないEng(England)、Swe(Sweden)、HOl(Holland)などと、逆のPor(Portugal)、Ita(Italy)、Aus(Austlia)、Spa(Spain)などを分ける軸になっています。
第二成分(縦軸)も同様に特徴づけして、foodsのデータ全体の差異の主な特徴を把握できます。
この主成分分析の結果を地図上に表示してみると、主成分の地理的な関係を把握したりできます。結果はこちらです。
主成分分析の結果をヨーロッパ地図上で表現してみた。
スクリプトは後日投稿します。
次に、Inst_Coffee を目的変数として、他の食品を説明変数として,pls, opls分析を実行してみます。
まず、Inst_Coffeeの列数を確認します。
colnames(foods)
出力結果

Inst_Coffeeは2列目なので、pls, oplsの目的変数yには2列目を指定し、他の列は説明変数xに指定します。
pls
Inst_Coffe.pls <- opls(x = foods[ , c(1, 3:20)], y = foods[ , 2], predI = NA, orthoI=0, crossvalI = 16, scaleC = "standard")
引数 x = foods[ , c(1, 3:20)] で Inst_Coffee以外の食品の列を説明変数に指定し、 y = foods[ , 2] で Inst_Coffeeの2列目を目的変数に指定します。
plsでは、preI = NA で予測軸の数を自動に設定、orthoI = 0 に設定します。
crossValI = 16 は 過学習を防ぐための交差検証(cross validation)での分割法の設定で、今回はサンプル数が比較的小さいのでleave-one-out法、すなわちサンプルをひとつずつテストデータとして交差検証させるので、サンプル数と同じ16に設定しました。
出力結果

R2x 0.549: は作成されたpls回帰モデルが説明変数の差異の54.9%を説明しているという意味になります。
同様に
R2Y 0.954: はpls回帰モデルが目的変数(Inst_Coffee)の差異の95.4%を説明しています。
Q2 0.579: は交差検証での平均値を示しています。
pre 3 : 作成された予測軸の数は3つです。予測軸の数の決定方法は以下の用に記載されています。
:either R2Y of the component is < 0.01 (N4 rule) or Q2Y is < 0 (for more than 100 observations) or 0.05
otherwise (R1 rule)
pR2Y = 0.05, pQ2 = 0.05: permutation testによるモデルの検定値です。
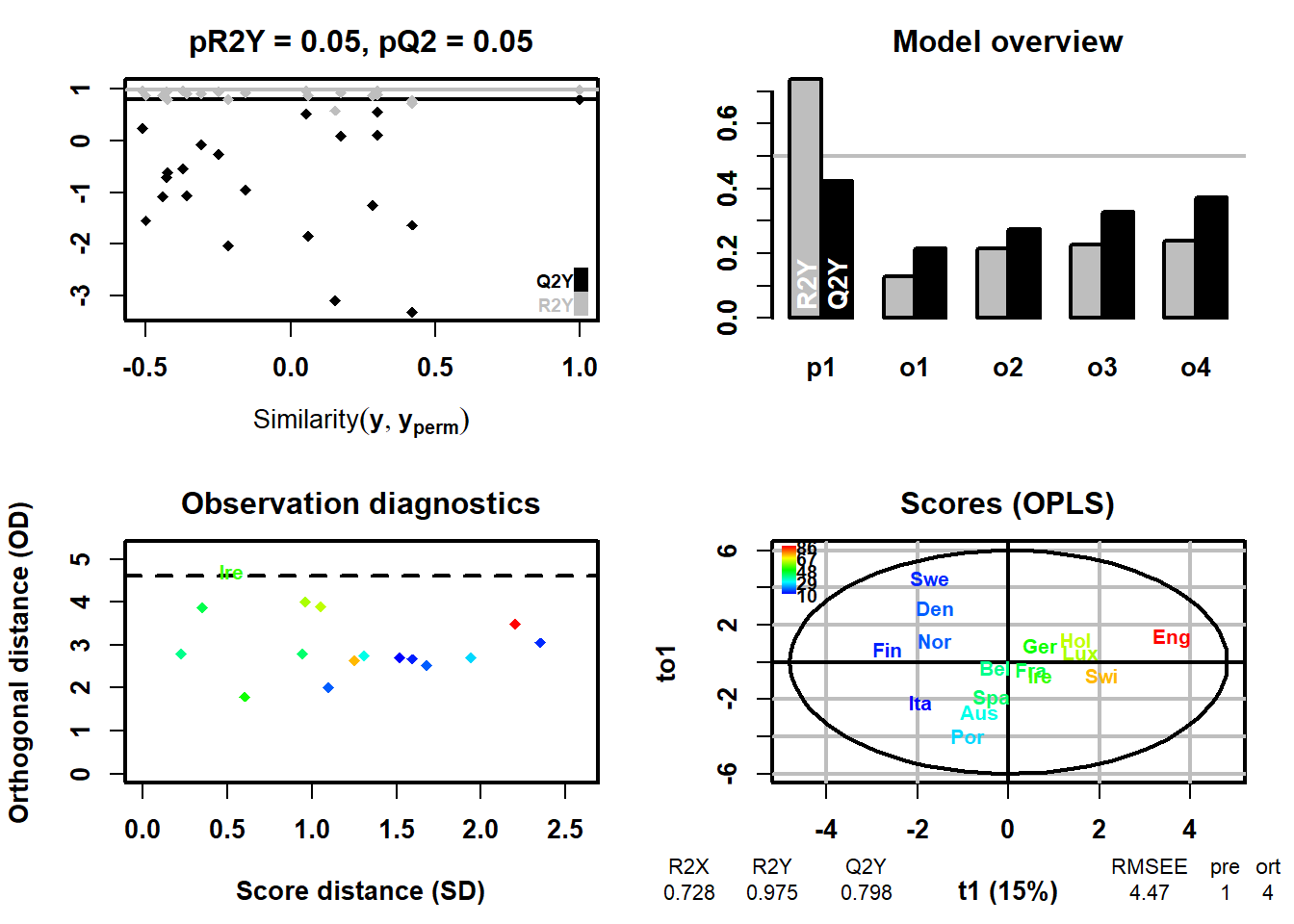
同時にサマリープロットが表示されます。
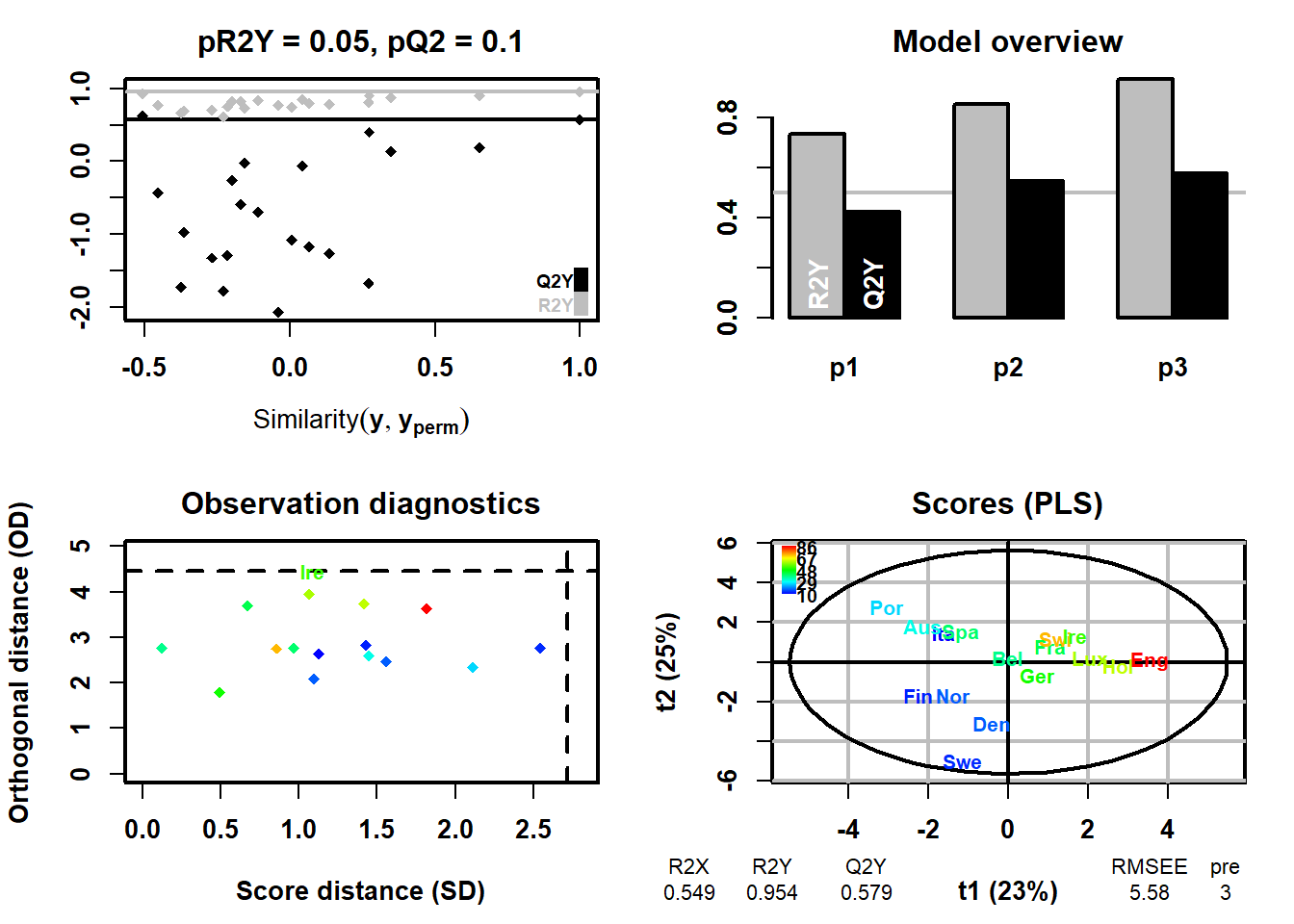
各プロットの詳細は次のopls分析で説明します。
opls
Inst_Coffe.opls <- opls(x = foods[ , c(1, 3:20)], y = foods[ , 2], predI = NA, orthoI=NA, crossvalI = 16, scaleC = "standard")
左上図permutation plot では作成されたOPLS回帰モデルの有意性を確認しますが、目的変数に関する決定係数R2Yのp値が0.05、予測能指標のQ2(Q2Y)のp値が0.05となっています。
右上図overview plotではInst_Coffe消費量の予測軸に対する直行軸が4つ作成されていて、それぞれの軸のR2Y、Q2Yへの寄与が確認できます。直行軸の数の決定については下記のように記載されています。
the number of orthogonal components is automatically computed by using the cross-validation (with a maximum of 9 orthogonal components)
左下図outoutlier plotでは、外れ値のサンプルの有無の確認をしますが、特に外れ値はありません。
右下図x-score plotではスコアプロットが、またプロットの下に作成されたモデルの指標のサマリーが確認できます。
R2X 0.728: 説明変数の差異の72.8%を説明している。
R2Y 0.975: 目的変数(ここではInst_coffeeの消費量)の差異の97.5%を説明できています。大変高い値です。
Q2Y 0.798: 交差検定の結果による予測能が0.798です。これもかなり高い値です。
上記の結果から、ヨーロッパ16か国におけるInst_coffeeの消費量は、他の食品の消費量で良い予測ができそうです。
roplsは様々なプロットや解析結果値を取り出す関数が充実しています。
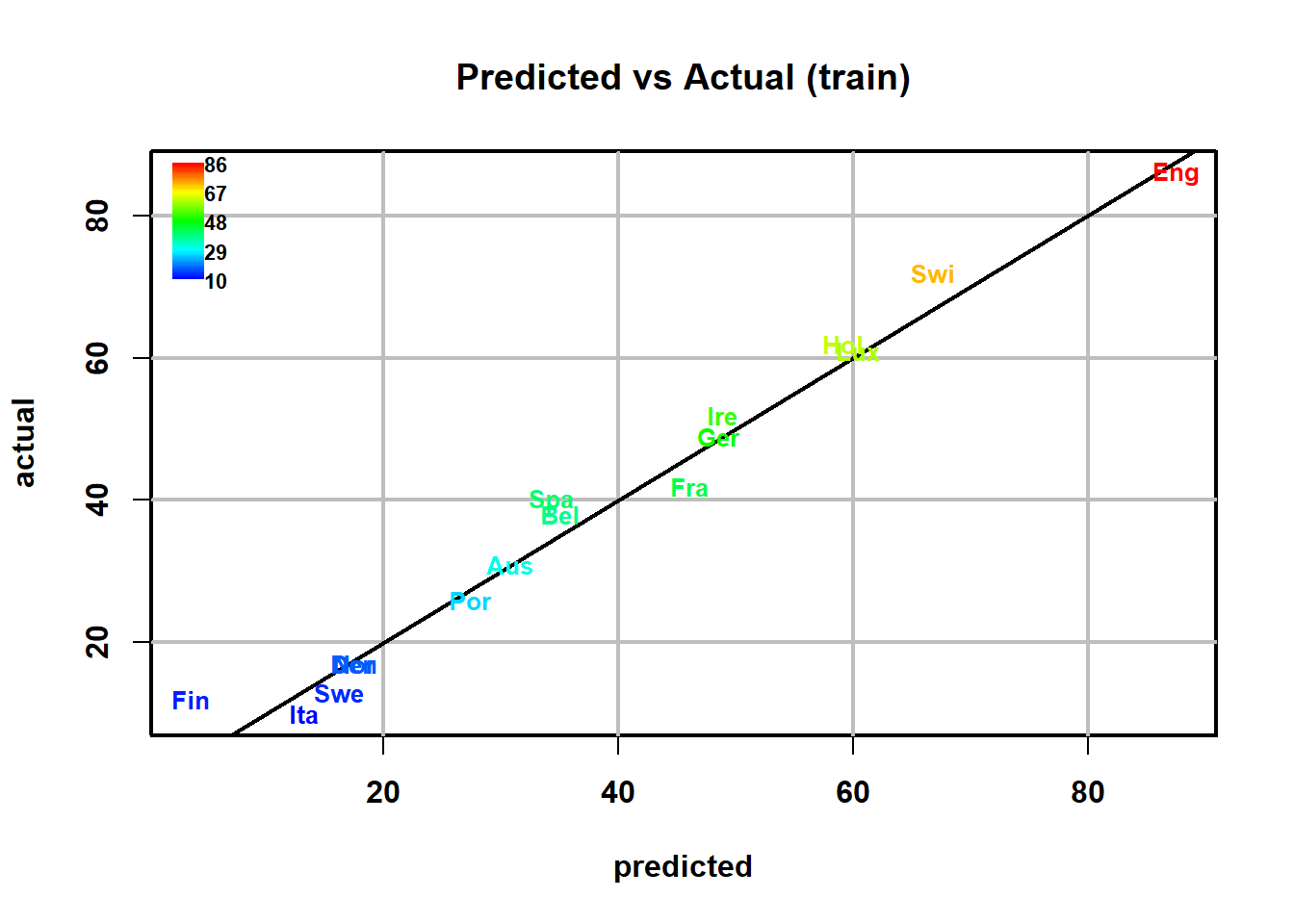
予測値vs実測値のプロットを作成することができます。
plot(Inst_Coffe.opls, typeVc = "predict-train", parCompVi = c(1,2))
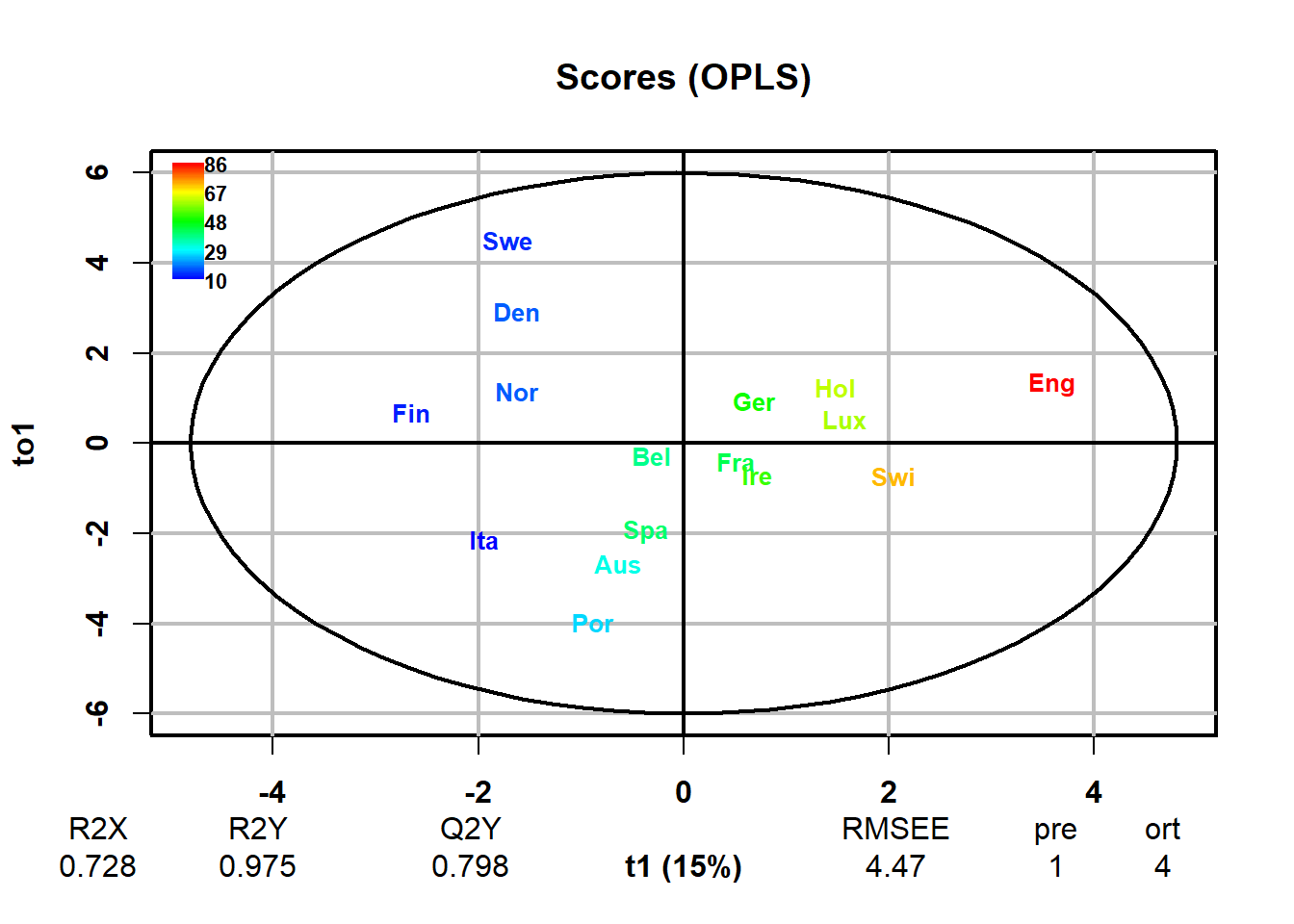
スコアプロットでヨーロッパ各国の関係を見てみましょう。
plot(Inst_Coffe.opls, typeVc = "x-score", parCompVi = c(1,2))
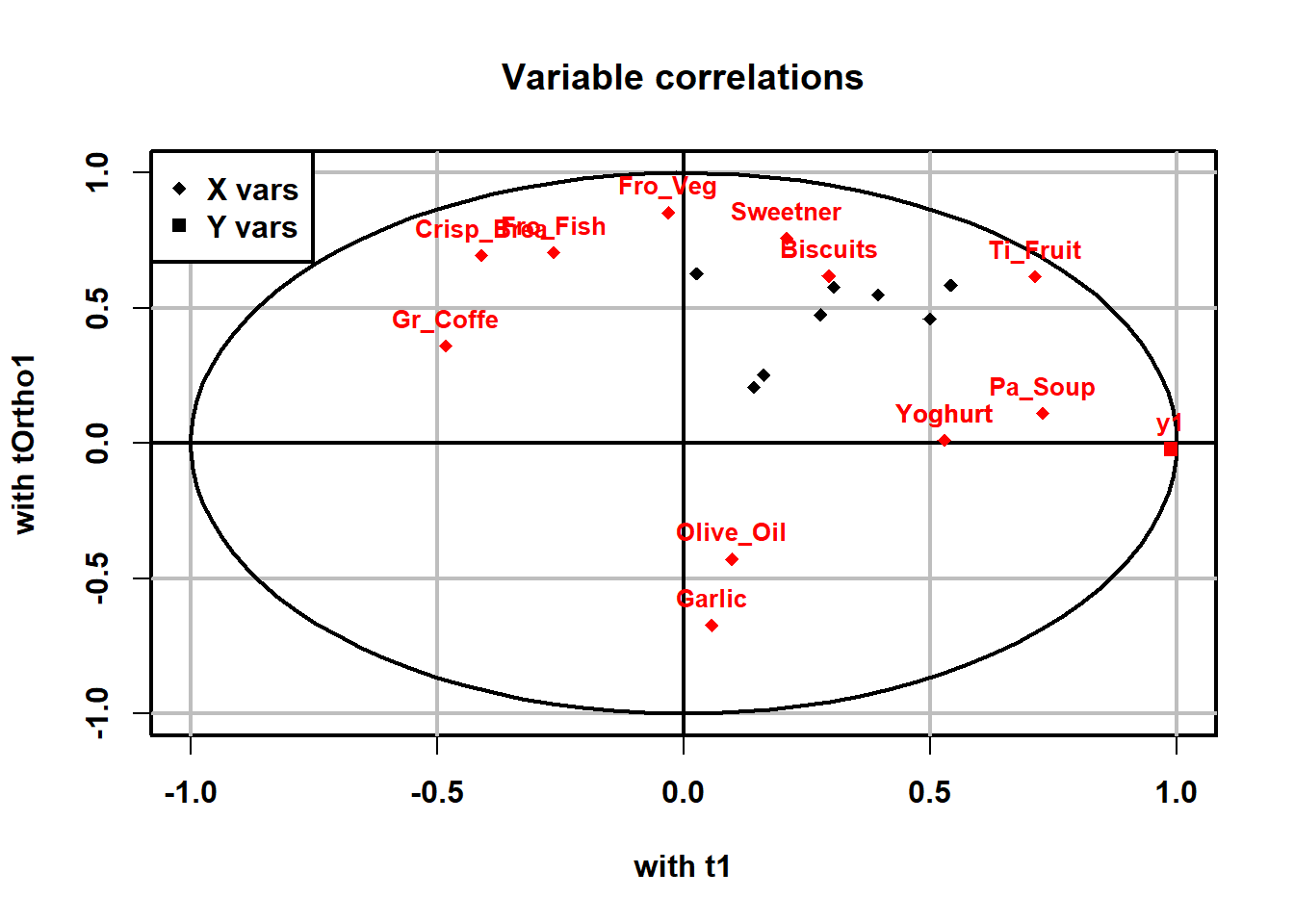
続けて、予測軸、直行軸と各食品との関係が分かり易い、相関プロットを作成してみます。
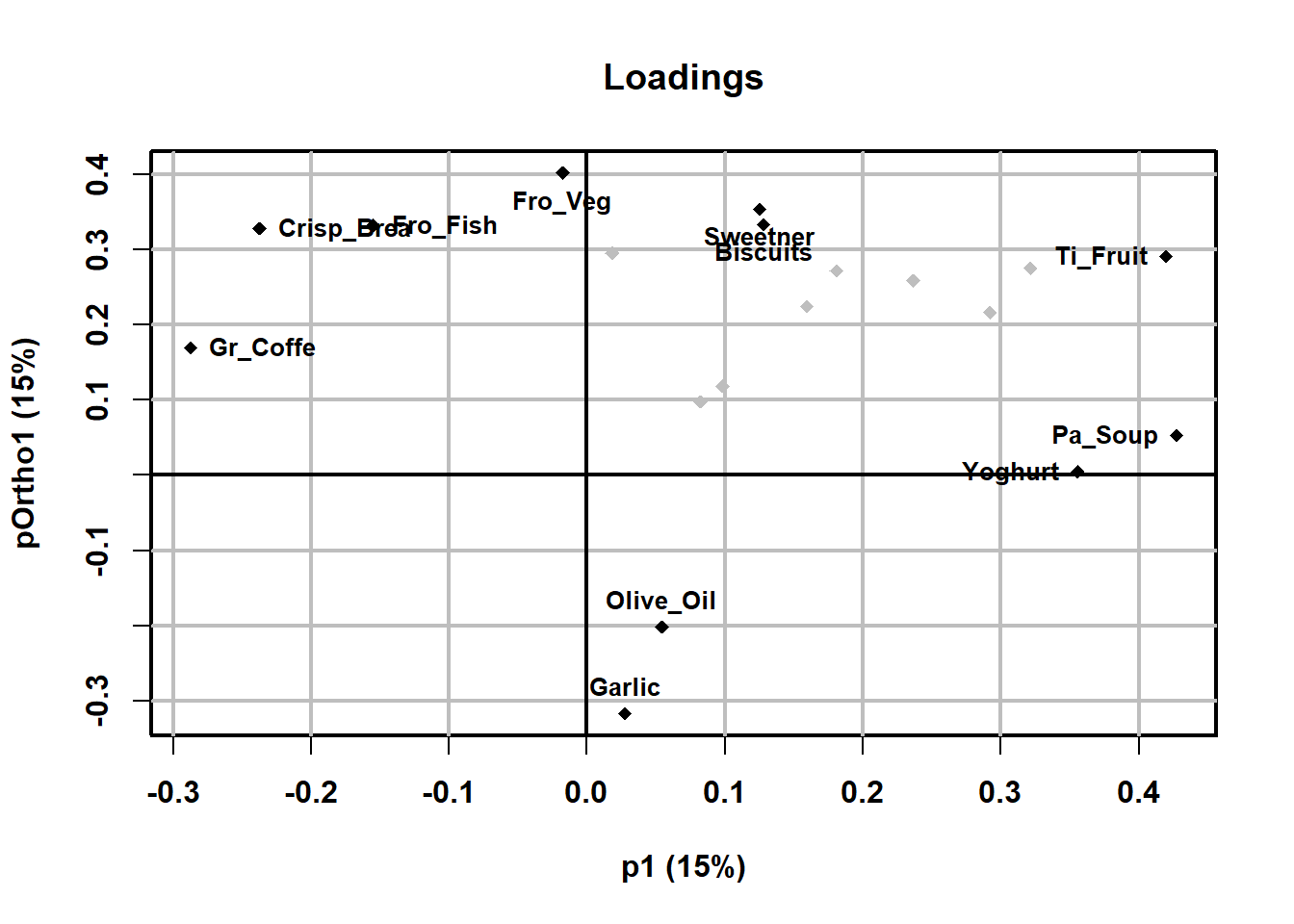
plot(Inst_Coffe.opls, typeVc = "correlation", parCompVi = c(1,2))
目盛りの単位が予測軸、直行軸との相関係数になっています。
このプロットから、Inst_Coffeeの消費の予測軸と正の相関が高いのは、Pa_SoupとTi_Fruit、Yoghurtであり、負の相関にGr_Coffeがあることがわかります。
また、直行軸tOtho1の特徴としては正の相関にFro_Veg、Sweetner、Fro_Fishが負の相関にGarlic、Olive_oilになっています。
スコアプロットと併せて解釈するとそれぞれの国の食品の消費の特徴がわかります。
直行軸は4つありますが、予測軸と2番目の直行軸でプロットしたい場合は、引数をparCompVi = c(1,3) と指定すれば良いです。
ローディングプロットも作成できますが、目盛りの単位以外はほぼ同じプロットが作成されます。
plot(Inst_Coffe.opls, typeVc = "x-loading", parCompVi = c(1,2))