古代の暗号をPythonで実装する

古代の代表的な暗号

シーザー暗号(シフト暗号)

暗号の実装

シーザー暗号はアルファベットを一定の文字数だけずらすことで暗号化する。またシフト数をNとするとROT N と呼ばれる。例えば3のときはROT3である。

caesar_cipher.py

# 暗号化
def encrypt(plain_text, shift_num):
	cipher = ""    # 暗号文
	for char in plain_text:
        if char.isupper():
            cipher += chr((ord(char) - 65 + shift_num) % 26 + 65)
        elif char.islower():
            cipher += chr((ord(char) - 97 + shift_num) % 26 + 97)
        else:
            raise ValueError("plainには英語を入力してください")
          
	return cipher

# 平文
plain  = "draemon"
# shift数,鍵
s = 3

print("Plain Text : " + plain)
print(f"shift_num : {s}")

try:
    print("cipher : " + encrypt(plain, s))
except ValueError as e:
    print(f"***ERROR***{str(e)}")

実行すると

terminal

% python caesar_cipher.py 
Plain Text : draemon
shift_num : 3
cipher : gudhprq

と暗号化できた。

ブルート・フォース・アタックで解読

英語は26文字しかないので、ずらし方は高々26通りしかない。

caesar_decipher.py

# ブルート・フォース・アタックで解読する
def decrypt(cipher_text):  
	for shift_num in range(26):
		answer = ""  # 鍵shift_numで復号したときの結果
		for char in cipher_text:
			# 英語以外のとき
                if not(65 <= ord(char) <= 90 or 97 <= ord(char) <= 122):
                    answer += char
                # 大文字かつシフトした際Aより小さくなるとき 
                elif ord(char) - shift_num < 65 : 
                    answer += chr(ord(char) - shift_num + 26)
                # 小文字かつシフトした際aより小さくなるとき 
                elif ord(char) - shift_num < 97 and ord(char) >=97:
                    answer += chr(ord(char) - shift_num + 26)
                # その他の場合 
                else:                                   
                    answer += chr(ord(char) - shift_num)

		print("鍵" + str(shift_num) + "で復号 → " + answer)


# 暗号文
cipher  = "Gudhprq"

# 解読
decrypt(cipher) 

これを実行すると

terminal

% python caesar_decipher.py
鍵0で復号 → Gudhprq
鍵1で復号 → Ftcgoqp
鍵2で復号 → Esbfnpo
鍵3で復号 → Draemon
鍵4で復号 → Cqzdlnm
鍵5で復号 → Bpyckml
鍵6で復号 → Aoxbjlk
鍵7で復号 → Znwaikj
鍵8で復号 → Ymvzhji
鍵9で復号 → Xluygih
鍵10で復号 → Wktxfhg
鍵11で復号 → Vjswegf
鍵12で復号 → Uirvdfe
鍵13で復号 → Thquced
鍵14で復号 → Sgptbdc
鍵15で復号 → Rfosacb
鍵16で復号 → Qenrzba
鍵17で復号 → Pdmqyaz
鍵18で復号 → Oclpxzy
鍵19で復号 → Nbkowyx
鍵20で復号 → Majnvxw
鍵21で復号 → Lzimuwv
鍵22で復号 → Kyhltvu
鍵23で復号 → Jxgksut
鍵24で復号 → Iwfjrts
鍵25で復号 → Hveiqsr

この中で意味の通るのは鍵3で復号したときである。

単一換字暗号

シーザー暗号はアルファベットをずらして暗号化したが、単一換字暗号はアルファベットを異なるアルファベットに置き換えることで暗号化する。例えば、平文がdraemonのとき、以下の対応表にそって暗号化するとjixborsとなる。

1	2	3	4	5	6	7
a	d	e	m	n	o	r
x	j	b	o	s	r	i

暗号の実装

今回は平文としてスティーブ・ジョブズの名言集の英語の名言を一つにまとめたtextファイルjobs_quote.txtを利用し、単一換字暗号で暗号化する。 ただし、簡単のため、アルファベット(大文字と小文字両方)のみだけで考える。

simple_substitution.py

import random
import re

# 暗号化する関数
def simple_sub_cipher():

    # アルファベットのASCIIのリストを生成する
	alphabets = [65 + i for i in range(26)] + [97 + i for i in range(26)]    
	new_alphabets = [65 + i for i in range(26)] + [97 + i for i in range(26)]

	random.shuffle(new_alphabets)      # ランダムに並び替える
	

	path = 'jobs_quote.txt'         # textファイルのpath
	with open(path) as f:
		words = f.read()      # textファイルの読み込み
		words = re.sub(r'[\W0-9_]', "", words)     # アルファベット以外全て消す

        # aから順に新たなアルファベットに置換していく
		for old, new in zip(alphabets, new_alphabets):
			words = words.replace(chr(old), chr(new))

		print(words)      #暗号化したテキストの表示


simple_sub_cipher()

実行すると

terminal

% python simple*
QPAacTWfDfDATDQTjAcTWaPLWQCPDfaHQcQfTGAAacafTTAQTLTFaHAAacaAacTWQLOaGOCGODcATTAATDaGQWATCGEATTAkDnALDEaCGEfTjATTAQQaODcfTTAQcCcVaHODEaAAaPCGcfTTAWaHQaODfGcATTACjTjAfHDPafWaHffafkTjCACjPafWaHfQaODfjQAjaGQWFWjTWCGEGaATTAWaHOTGOaGODGAfTADaGATDATCGEjATTATfDfDTQQWCLnafATGAVaHOTGAOaGGDOAATDcaAjQaakCGEPaffTfcWaHOTGaGQWOaGGDOAATDLQaakCGEFTOkfTfcjEaWaHTTODAaAfHjAATTAATDcaAjfCQQjaLDTafOaGGDOACGWaHfPHAHfDQLATDaGQWnDfjaGQkGafATTAjQajATIHTfADfaPTFCQQCaGcaQQTfjCGaGDWDTfQAjODfWOTTfTOADfFHCQcCGEECLnQDOTGFDTTfcDfATTGOaLnQDqVaHTTODAafafkTTfcAaEDAWaHfATCGkCGEOQDTGAaLTkDCAjCLnQDbHACAjfafATCACGATDDGcFDOTHjDaGODWaHEDAATDfDWaHOTGLaODLaHGATCGjQAjfDTQQWTTfcAacDjCEGnfacHOAjFWPaOHjEfaHnjfQaAaPACLDjnDanQDcaGAkGaffTTAATDWfTGAHGACQWaHjTafCAAaATDLbDCGEATDfCOTDjALTGCGATDODLDADfWcaDjGALTAADfAaLDHaCGEAaFDcTAGCETAjTWCGEfDODcaGDjaLDATCGEfaGcDfPHQATTAjfTTALTAADfjAaLDnTDOHfDPaffnnQDCjGaAOajAOHAACGEnTDOHfDPaffnnQDCjAaCGGaOTADCAjfTWaHAaPCAjOHffDGAnfDcCOTLDGAnTDaGQWfTWAacaEfDTAfafkCjAaQaODfTTAWaHcaQPWaHTTODGAPaHGcCAWDAkDDnQaakCGEcaGAjDAAQDfjfCATTQQLTAADfjaPATDTDTfAWaHQQkGaffTDGWaHPCGcCAVaHfOHjAaLDfjcfDTLaPTTTnnCDfTGcFDAADfQCPDcaGALaODnfacHOAjWGfCOTQCODjEATWTHGEfWEATWPaaQCjTQfaHQcAfTcDTQQaPLWADOTGaQaEWPafTGTPADfGaaGfCATEaOfTADjKDLDLFDfCGEATTAWaHTfDEaCGEAacCDCjATDFDjAfTWQkGafAaTOaCcATDAfTnaPATCGkCGEWaHTTODjaLDATCGEAaQajDCHTQCAWCjLafDCLnafATGAATTGIHTGACAWLGDTaLDfHGCjLHOTFDAADfATTGAfacaHFQDjEaLDACLDjfTDGWaHCGGaOTADWaHLTkDLCjATkDjQACjFDjAAaTcLCAATDLIHCOkQWTGcEDAaGfCATCLnfaOCGEWaHfaATDfCGGaOTACaGjQGGaOTACaGcCjACGEHCjTDjFDAfDDGTQDTcDfTGcTPaQQafDfcaWaHfTGAAajnDGcATDfDjAaPWaHfQCPDjDQQCGEjHETfDcfTADfafcaWaHfTGATOTTGODAaOTTGEDATDfafQcVaHfACLDCjQCLCADcjacaGAfTjADCAQCOCGEjaLDaGDDQjDjQCPDcaGAFDAfTnnDcFWcaELTfTCOTCjQCOCGEfCATATDfDjHQAjaPaATDfnDanQDjATCGkCGEcaGAQDAATDGaCjDaPaATDfjanCGCaGjcfafGaHAWaHfafGCGGDfOaCODfGcLajACLnafATGATTODATDOaHfTEDAaPaQQafWaHfTDTfATGcCGAHCACaGnTDWjaLDTafTQfDTcWkGaffTTAWaHAfHQWfTGAAaFDOaLDWODfWATCGEDQjDCjjDOaGcTfWbDTWTfcjACOkaPIHTQCAWEaLDnDanQDTfDGAHjDcAaTGDGOCfaGLDGAfTDfDDqODQQDGODCjDqnDOADcQLTjnfaHcaPfTTAfDcaGAcaTjQTLaPfTTAfDcaQcCcGAjDDCAATDGFHACAAHfGDcaHAATTAEDAACGEPCfDcPfaLfnnQDfTjATDFDjAATCGEATTAOaHQcTTODDODfTTnnDGDcAaLDnTDTDTOCGDjjaPFDCGEjHOODjjPHQfTjfDnQTODcFWATDQCETAGDjjaPFDCGETFDECGGDfTETCGQDjjjHfDTFaHADODfWATCGEQAPfDDcLDAaDGADfaGDaPATDLajAOfDTACODnDfCacjaPLWQCPDQPWaHQCODDTOTcTWTjCPCAfTjWaHfQTjAjaLDcTWWaHQQLajAODfATCGQWFDfCETAVaHOTGAjHjATjkOHjAaLDfjfTTAATDWfTGATGcATDGAfWAaECODATTAAaATDLbWATDACLDWaHEDACAFHCQAATDWQQfTGAjaLDATCGEGDf

意味不明な文に暗号化できた。

頻度分析で解読

頻度分析とは文字の頻度を調べてることである。

例えば頻度分析のWikipediaによれば、一般的に1番よく使われているのはeである。2番目にi,3番目にa,4番目にt,5番目にnがくる。

ここで先ほどのjobs_quote.txtを頻度分析してみる。

frequency_analyzer.py

import re

path = 'jobs_quote.txt'  # pathの設定
with open(path) as f:
	words = f.read()   # ファイルの読み込み
	words = re.sub(r'[\W0-9_]', "", words).lower()

	char_set = { alphabet for alphabet in words } # 一文字づつ分ける
	char_freq = { alphabet : words.count(alphabet) for alphabet in char_set }  # 文字の回数を数える

	sorted_char_freq = sorted(char_freq.items(), key = lambda x:x[1],reverse = True)    # 頻度の多い順に並び替え

	print(sorted_char_freq)   # 表示する

実行すると

terminal

% python freq*             
[('t', 285), ('e', 269), ('o', 244), ('n', 172), ('a', 168), ('i', 167), ('s', 128), ('r', 122), ('h', 118), ('l', 92), ('u', 89), ('y', 85), ('d', 84), ('m', 66), ('w', 64), ('c', 60), ('g', 55), ('f', 47), ('p', 39), ('v', 34), ('b', 32), ('k', 23), ('q', 5), ('x', 3), ('j', 1)]

となった。先ほどのWikipediaの頻度分析結果と全く同じではないが、名言であるということも考慮すると結構似ている結果となった。

ちなみにtとeが分かれば英語でよく使われるthe,they,he,getなどが推測しやすくなる。これを地道に頑張っていくと解読できる。

その他の歴史的な暗号

ROT13

シーザー暗号のシフト数を13にしたものである。

平文をxとすると

ROT_{13}(ROT_{13}(x)) = ROT_{0}(x)

アルファベットは26個なのでROT13を2回すると下の文に戻る。
ravine をROT13変換すると enivarなど言葉遊びなどに使われる。

>>> import codecs
>>> codecs.decode('abc', 'rot13')
'nop'

ヴィジュネル暗号

アルファベットを1つずつずらした以下のような表ヴィジュネル方陣と呼ぶ。

例えば平文が'DRAEMON'のとき、鍵を'ABC'とするとDはA行D列のD, RはB行R列のS, AはC行A列のCとなる。平文がが鍵よりも長い場合、鍵を繰り返して使う。つまり次のEはA行E列のEとなる。これを繰り返すとDSCENQNと暗号化される。
鍵の周期(今回なら3)を知られないことが大事である。

ここでa=0, b=1,..., z=26, piは平文のi文字目、Kiは鍵のi文字目, Ciは暗号文のi文字目とすると

C_i = (P_i + K_i)mod26

ちなみに復号化も同じように表すと

P_i = (C_i - K_i)mod26

となる。

この解読方法はカシスキー・テストと鍵推理による解読法がある。

カシスキー・テストは鍵の繰り返しに注目するため、非常に長い(長さが平文の約1/2以上)ときには使えない。

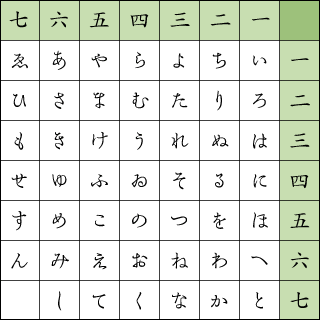
上杉暗号

ヴィジュネル暗号のように、平仮名を7マス四方の表に入れて縦横に数字を割り振り、平仮名に対応する数字で暗号化する。

例えばすねおは七五 三六 四六と暗号化される。