Single responsibility principle
SOLID原則、およびそれに含まれるS:Single responsibility principle(SRP) というものがあります。
一つのクラスは単一の責務だけを持つ。
またはその派生として
クラスを変更する理由は一つでなければならない。
ここで問題となるのが「一つ」とは何か?です
SOLID原則(とSRP)を紹介する記事は沢山ありますが、「じゃあ具体的に一つの責務ってなんだ」かを書いてある記事は見たことがありません。
一つのメソッドしか持たないクラスとか一つの変数しか持たないクラスでしょうか?でもそんなコードは見たことが無いですよね?
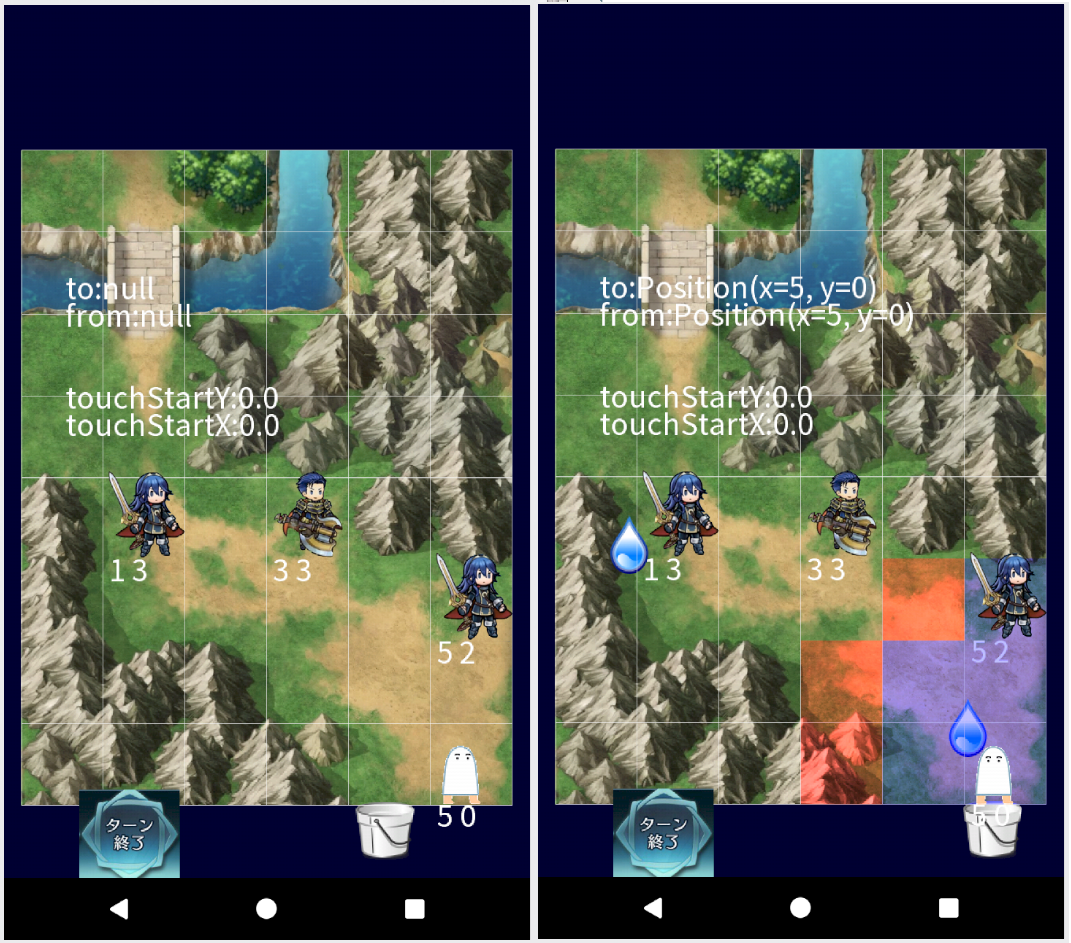
そこで実際にSRPを守りながらモデルを設計してみましょう。今回モデル化するのもやはりファイアーエムブレムヒーローズ(FEH)ですが、今回はそのUI、将棋盤のような画面をモデル化します。なぜなら、この「将棋盤」というのは将棋という他のゲームのルールの再利用であり、今後も他のゲームで採用されることがあり、正しくモデル化すれば他のゲームでも同じモデルが再利用できるからです。
最終的にはこうやってAndroidで動かせるようになるところまで解説する予定です。
あなたは「もっとも抽象的な盤」に何をすることができるか?
さて将棋盤をモデル化するので将棋盤の実物が欲しいところですが、普段から将棋盤が手元にある人は少ないんじゃないでしょうか。そこで盤のような紙で代用しましょう。紙とそれよりは小さな何かを用意してください。鉛筆とか消しゴムとか。
さてここで問題です。「盤」と「それよりは小さな何か」でできることはなんでしょうか?
正解は「盤の上にそれを載せる」「盤の上に載っているそれを取り除く」です。
「何か」ではなく「鉛筆」であれば紙に何か書いたりもできるのでしょうが、「何か」では書くことができるかもわからないのでできません。真に抽象的なオブジェクトはそれに何ができるかが限定されていないので事実上何ができるとも言えません。
事実上何もできません…が、すべてのオブジェクトは他のオブジェクトと関連付けられる可能性があることが知られています。今のところ「どんなオブジェクトとも関連付けられないオブジェクト」は見つかっていません。また、オブジェクトと関連付けられるということは関連付けないこともできるということです。すべてのオブジェクトは直接的または間接的に関連してるとか色々な言い方があるのですが全部同じことです。
そして、関連の仕方はオブジェクトの種類(クラス)によります。特定のクラスではない何らか(Any)のオブジェクト(Object)は「何らかの関連」を持つことになります。
今回は片方が「盤」であることが決まっているので、「何かを載せる/載せない」という形で関連付ける/付けないことができるという事でいいでしょう。
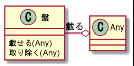
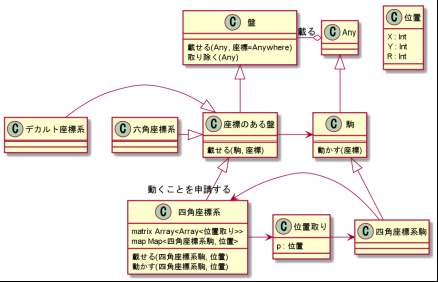
よってクラス図はこんな感じになります。
このように抽象化することで「関連付ける」単一の機能だけに絞りましたがメソッドとしては一つにはなりませんでした。無理して「関連付ける/付けない」を「関連付ける/Null付ける」にすると1メソッドで書けるのですがこれは「関連がNullとはどういうことか?」という新たな問題を引き起こします。なぜ二つのメソッドなのに許されるかは別の話の後のほうが分かりやすいので後述することにしてこのまま進めます。
あなたは盤上の駒を動かすことができるか?
さて、盤の上には何かを載せることができることが分かりました。
ですが将棋というのは駒を並べるところが始まりで、交互に駒を動かして遊ぶものです。では、盤上に載せた「何か」は動かすことができるでしょうか?
あなたが(真面目なことに)紙と「何か」を用意していたら、紙に載せた「何か」を動かせることがわかるでしょう。これで解決ですね!…とはもちろんいきません。
いや動かせるといえば動かせるのは確かなのですがどう動いたかを確認する方法が無いのです。
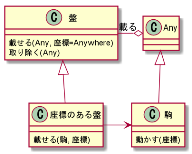
つまり、「何か」を動かすには「どこからどこへ動いたかわかる盤面が必要」という事になります。具体的には「座標のある盤」ならばどこからどこへ動いたかわかるのでこれを作ることになります。
ではさっそく「座標のある盤」を作りたいところですが…
「座標のある盤」とは「座標を持っている盤」のことでしょうか?つまりメンバーとして座標を持っている盤という合成(コンポジション)になるのでしょうか?仮にそうであるとすれば座標は盤の部分になる、盤から座標を分離することができるという事になります。これはちょっと想像がつきませんね。
もっとわかりやすいのは「座標が存在しないため何処か指定せずにおくことができる盤」に「座標が存在し、必ずいずこかに置かなければいけない盤」という制限を加えることです。つまり、座標があるという事は座標という部分を持つのではなく座標に束縛されるという制限を追加することになり、座標のない盤を継承して座標のある盤を作るという事です。一般に継承よりは合成を使おうという話になっていますが、このように制限や束縛を追加したいときは合成は使えません。合成は分割できるものにしか使えないのです。
ところでこの記事の冒頭、SRP「クラスを変更する理由は一つでなければならない」を覚えていますか?
この「座標のある盤」は「どこからどこへ動いたかわかる」ようにしたいというたった一つの理由から作成されるものですので、まさにこの条件にふさわしいものだといえるでしょう。
あなたは盤上の駒をどこへ動かすのか?
長くなりましたが盤を継承して「座標のある盤」を作れば解決ですね!
と言いたいところですがまだ問題はあります。座標が駒の位置を示すものだという事は決まりましたが「具体的に座標とは何か」がまだ決まっていないのです。
将棋盤なので9x9の升目を持った格子状の座標なのですが、ボードゲームでよく使われる座標は数種類というかぶっちゃけ「三角形」「四角形」「六角形」のいずれの升目を持つ、または升目ではなく座標軸を持つデカルト座標系があるという事が知られています。
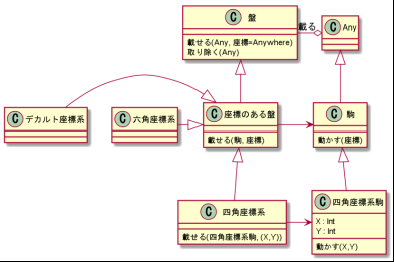
よって「座標のある盤」をさらに継承して「特定の座標系を持つ盤」を作るのでクラス図はこうなります。これを「特化」と言います。あ、座標のある盤を抽象クラスにするの忘れてた…
駒を置いたり移動したりすることは座標系によらずできますが、じゃあどこに動くかという座標のほうは具体的な座標系によるので「座標のある盤」のメソッドではまだわかりません。のでこれは抽象メソッドとなります。
常識的に考えるなら将棋盤をモデル化する際には座標のない盤はあまりにも役に立たないので無視してこの座標を持つ/特定の座標系を持つ盤からスタートしていいでしょう。
ところで座標系を持つ盤があったとして、そこに配置した駒の座標は誰が管理すべきでしょうか?盤が持ってもいいのですが駒ごとにそれぞれの座標に位置するので駒が持つのが自然に見えますね。今までは特に場所を指定せずにおかれていた「何か」であったのでこれに座標を追加して「駒」にしましょう。これが囲碁だったら駒ではなく石のような気もしますがそこはちょっと目をつぶって「配置された何かは駒である」という事にしてしまいましょう。
ところで駒が座標を持つことにしましたがこの場合の具体的な座標は普通格子状にしろデカルト座標系にしろ縦横/XYで表現されます。あれ?変数が二つある…これもSRP違反でしょうか?
一つの責務の一つとは one ではなく individual (分解できない)
簡単な言葉ほどニュアンスが違ったり実は難しい概念であるというのはよくある話で、「一つ」というのもそのうちの一つです。
形而上学的な意味で「一つ」というのは「カウントして一つ」という意味ではなく、「それ以上分解できない一つ」という意味です。
つまりXとYで変数が二つあるか?というのは間違いで、XとYの組は分解できるか?というのが正しい問いとなります。先述した「関連付ける・付けない」も「関連付けないだけの何か」に分解することができないため、一つとしていいということですね。
XY平面をXとYに分けることができるか?は私は数学が分からないので数学者に聞いて欲しいですが、縦しかなく横幅のない将棋盤、幅が1ならともかく幅が0の将棋盤はもはや将棋盤の部分ですらなく、駒を載せることもできません。
よって将棋盤としての存在は縦と横を分解することはできないと考えるべきでしょう。
これでXとYは一つの組という事で分解することができず、オブジェクト中に共存していいという事が分かりました。他にもないでしょうか?どうせ分解できないものならこの機会に入れておきたいものです。
将棋の駒を見る限り向き、方向があるようです。チェスのポーンは見た目では向きが無い気もしますが進む方向は相手陣地のみなのでやはり向きがあるといえるでしょう。FEHに向きはありません…敵と味方で顔の向いている方向は違いますが移動の際には向きは関係ありません。が、これは無いというより向きはどうでもいいと考えるべきでしょう。数学的にもある座標からある座標を引いたものは方向として扱われるので向きはあるといえるでしょう。方向がどうでもいいゲームは存在するでしょうが、方向が存在しえない将棋盤はないので駒は向きを持っても良いという事になりそうです。
とりあえずXYと向きを合わせて「位置」とでもしましょうか。
向きはRとでもしましょう。デカルト座標系ならばラジアンを使うところでしょうが、ゲームではある方向を0として右もしくは左回りに1枡ごとに番号を割り振るのが一般的かと思います。六角形でも同じ構造が使えます。一周は四角では0-3または斜めを入れて0-8、六角では0-5になります。
なお向きは使わないゲームも多いので初期値0を入れてしまってもいいでしょう。いっそのこと使わないうちはなくてもいいです。必要になってから項目を追加しても全く困りません。
data class 位置(x : Int, y : Int, r : Int = 0)
大きさもほとんど問題になることはないですが、大きさのない将棋盤なるものは存在しえないのであっていいでしょう。駒が複数の枡にまたがったり逆に複数の駒が一つの枡に共存することもあります。デカルト座標系のゲームだったら専有面積や当たり判定があることのほうが多いでしょう。これも使わないゲームのほうが多いので使うまでなくていいでしょう。
ただしここで大問題が発生します。例えば-1とか盤の外に配置できるか?同じ場所に別の駒が存在し得るか?という問題です。
オブジェクトは自分の債務を持つが必ずしも決定権は持たない
一つの枡に複数の駒を入れられるか入れられないというのは個々のゲームにおけるルールでしかありませんが、破ることも例外を設けることも許されないルールです。
仮に駒が自分の位置を自由に設定することができる場合、いつかそれは他の駒の位置とぶつかるでしょう。また単に盤外は乗せたことにならないでしょう。つまり駒は自分の位置を決めてはいけません。
fun 駒.move(p : 位置) {
this.p = p
}
みたいなコードは誰でも「駒.move(位置(0,0))」を実行できるため書いてはいけないという事になります。実際にこの構造にすると「未初期化なのでとりあえず0,0に置く駒」が続出して0,0に多くの未初期化駒が積みあがることになります。
じゃあどうするのかっていうと private にして外部からのアクセスを禁止します。
class 駒(var p : 位置){
private fun move(p : 位置){
this.p = p
}
class 将棋盤{
fun move(o : 駒, p : 位置){
if (盤内のとき && 他の駒が無いとき) {
o.move(p)
} else {
throws Exception
}
}
}
}
move()をprivate にすると同時に将棋盤もprivate にします。private にすることで同じ内部のオブジェクトである将棋盤からしか位置を変更できなくなります!
メソッドを特定のクラスにのみ公開する言語機能が欲しい…JavaならProtectedで同じパッケージに限定できたのに……いや流石にこれはやりすぎですね。
もっと簡単な解決方法はいくつかあります。
コメントで使用不可にするのが一番簡単な解決方法でしょう。
/** 将棋盤専用。駒自身からですら使用禁止 */
fun 駒.move(p : 位置) {
this.p = p
}
正しくモデル化すればコメントは要らないなんて言う人もいますが「そのデータを誰が管理するのか」は言語機能に負うところが大きいので正しくモデル化できるとは限りませんのでコメントで補う必要があります。しかも西洋人はオブジェクトは属性を持ち、その属性を管理する責任を持つというメタモデルを作ってしまったのでたまに変なことになります。例えばJavascriptとかで必要ないのにやたらClassを作ろうとしたりプロパティをprivateにしたがったりします。
実をいうと物体が位置を属性として持つという認識自体が間違いというか最初に「物体が位置を属性として持つ」と言ったのはアリストテレスですが、同時に「複数のオブジェクトの関係をオブジェクトの属性とすると片方を変更したときにもう片方も正しく変更される保証がなくて上手くいかないわテヘペロ」とも言ってます。だいたい2500年前の話です。
ある空間に複数のオブジェクトが存在する場合は空間がオブジェクトへの支配権を持つほうが簡単にモデル化できます。
その場合、位置というのはある空間における存在は位置にMapできるっていうのが正しい表現になるでしょうか?とりあえずやってみましょう。
class 将棋盤{
data class 位置取り(val o : 駒?, val p : 位置)
val map = mapOf<駒, 位置>()
val matrix = MutableList<MutableList<位置取り>>
fun move(o : 駒, p : 位置){
if (盤内のとき && 他の駒が無いとき) {
val old = at(o)
matrix[p.x][p.y] = 位置取り(o, p)
matrix[old.p.x][old.p.y] = 位置取り(null, p)
map[o] = p
} else {
throws Exception
}
fun at(o : 駒) : 位置? = map[o]
}
こんな感じで将棋盤に位置情報を格納したほうが簡単に実装出来ますし構造も単純になります。位置とオブジェクトが直接Mapされるため、位置は物理的に空間側が持ちコントロールを持ってるという違いだけでオブジェクトの属性であるのとほぼ同義です。
このとき利便性のためmatrixとmap、の両方で位置取りを保持したいところです。移動によくあるバグとして「元の位置と先の位置の両方に存在する」ってのがあるため元の位置から駒を除去したりするのに使います。2重にデータを持つことになりますが、同じ場所で「のみ」変更する分には最小単位のトランザクションとなり、問題は滅多に発生しませんし簡単にテスト出来ます。
同じエリアに複数の駒が配置できる場合はエリアが保持する駒が当然複数になります。
繰り返しますが、これは位置関係の支配権を空間側が持っているからこんな面倒な話になるのであり、オブジェクトがどこに配置してもOKだったり重なったりしてたりしてもいいなら単純にオブジェクト側に位置を持たせていいでしょう。
ゲーム的には駒を動かすときに駒から盤へ動きを申請する形にすると「駒を特定の位置へ動かす」「それを盤が判定する」の両立ができますし、返り値として駒側に位置を返すことで駒も自分の位置を知ることができます。他のオブジェクトにより移動させられることもあるためその位置の正しさは限定的ではありますが、画面表示に使うとか使い道は結構あります。
余談ですが、今回は枡ですがデカルト座標系でもこの構造が有効です。特に大きさを持ち、オブジェクト同士が重ねられないときは位置関係を盤がコントロールしなければなりません。
また、速度的にも有用なことがあります。具体的にはシューティングゲームを作る際には当たり判定が必要になるのですが、これが弾幕系だと画面内に数百の弾が飛び交う事になり全ての弾の当たり判定をとるとめっちゃ重くなります。そこで画面をMatrixに区切って弾を格納し、自機に近い弾とだけ判定するようにします。例えば画面を16x16の256分割し、自分とその周りで9マス内にある弾とだけ判定をすれば対象は期待値で9/256となり判定回数がそれなりに減らせます。
これで将棋盤上のどこにでも(他の駒が無ければ)移動できるようになりました!
…でも将棋にしろFEHにしろどこにでも駒を動かせるゲームじゃないですよね?
じゃあ「どこに駒を動かせるか?」は誰の責務でしょうか?
まあこれは常識的に考えて駒の責務になりますよね。「歩は一歩前に進める」とかそういう話です。つまり駒は「自分の移動範囲を管理できる」という責務を持ちます。
じゃあ駒を継承して「移動制限をもった駒」を作りたいところですが移動制限があるにしろその実装は駒の種類によるので直接継承は避けたいところです。
例えば、将棋の駒を使ってチェスを遊ぶこともできなくはありません。将棋の駒が無ければ紙に書いたって良い。つまり、盤上の駒と駒の種類は実のところ別のものです。
駒が移動範囲を持つ、だが移動範囲は駒の種類による。という構造にして移動範囲の計算を駒の種類に移譲するほうが分かりやすいでしょう。移動範囲というよりいっそ「駒の能力」にしときましょうか。この形にしたほうが駒はそのままで能力を取り換えたりできますし融通が利きます。例えば駒が成るときは成っているかを判定するよりは駒の能力を取り換えてしまったほうが早いです。
というわけで移動する駒を設計したいところですが予想より長くなったので区切ります。これだけ書いてまだコード数行か参ったな…!