Python で自動微分 & 非線形力学系の数値計算

非線形力学の分野で, 固定点の安定性を議論する際に線形安定性解析を行います. 例えば Brusselator 方程式 を例に取ると, その力学系は次式で表されます ( $a,b$ は正の定数 ) .

\begin{equation}
\begin{aligned}
&\dot{x} = f(x,y) = a-(b+1)x+x^2y\\
&\dot{y} = g(x,y) = bx-x^2y
\end{aligned},\qquad x,y\ge 0
\end{equation}

この方程式系の固定点を $(x,y)=(x^*,y^*)$ とおくと, 線形安定性解析により固定点 $(x^*,y^*)$ における安定性は次のヤコビアンの行列式と対角和を計算することにより議論できます.

\begin{equation}
\frac{\partial (f,g)}{\partial (x,y)}=
\left(\begin{aligned}
&\frac{\partial f(x,y)}{\partial x}&\frac{\partial f(x,y)}{\partial y}\\
&\frac{\partial g(x,y)}{\partial x}&\frac{\partial g(x,y)}{\partial y}\\
\end{aligned}\right)_{\begin{aligned}x=x^*\\y=y^*\end{aligned}}
\end{equation}

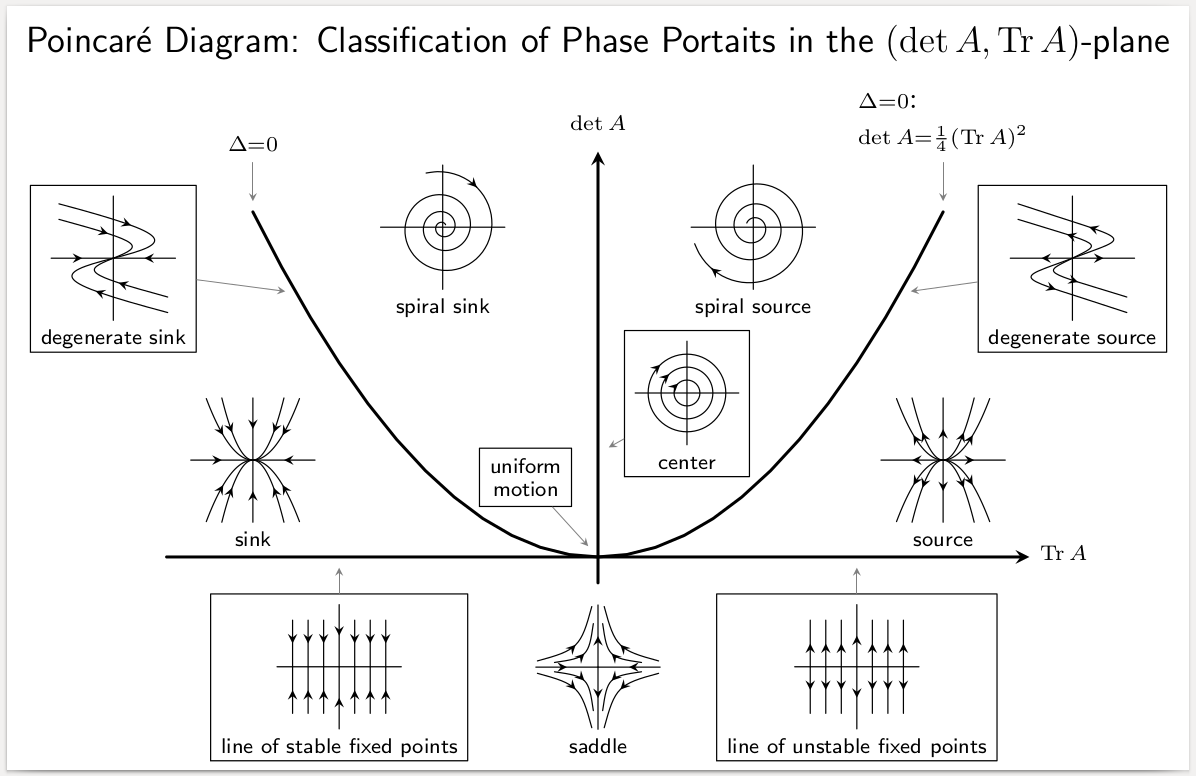
次の図は, 固定点における対角和と行列式の値によりその固定点の安定性を分類するダイアグラムです.

遊びで様々な 2 変数の非線形力学系を数値計算する際, その方程式毎に関数 $f(x,y),g(x,y)$ を解析的に偏微分してプログラムに記述するのは少々面倒です. そのため今回は, 偏微分の計算をプログラムに行わせるために二重数による自動微分を用いました. python で二重数を用いるために作成した module ( dual.py ) のソースはこちらに上げておきます. 以下が任意の $x,y$ における対角和と行列式を計算するために定義した関数です.

from dual import *

def calc_trace_determinant2(x,y):
    det = fx(x,y)*gy(x,y)-fy(x,y)*gx(x,y)
    tr = fx(x,y)+gy(x,y)
    return tr,det

def fx(x,y):
    return dual(f(dual(x,1),y)-f(x,y)).im

def fy(x,y):
    return dual(f(x,dual(y,1))-f(x,y)).im

def gx(x,y):
    return dual(g(dual(x,1),y)-g(x,y)).im

def gy(x,y):
    return dual(g(x,dual(y,1))-g(x,y)).im

# Brusselator 方程式の場合, f, g は次のように定義する.
# 引数x, yにはスカラーを指定してください.
def f(x,y):
    return a-(b+1)*x+x**2*y

def g(x,y):
    return b*x-x**2*y

また, 線形安定性解析では固定点における対角和と行列式の値を知りたいため, ニュートン法を用いて次の関数により固定点の座標を取得しました.

import numpy as np

def newton_method2(f,g,x_range,y_range,epsilon=10**(-13),limit=10**4):
    x_min,x_max = x_range
    y_min,y_max = y_range
    x = np.random.rand()*(x_max-x_min)+x_min
    y = np.random.rand()*(y_max-y_min)+y_min
    err_x,err_y = 1,1
    count = 0
    while err_x>epsilon or err_y>epsilon:
        _,det = calc_trace_determinant2(x,y)
        dx = (fy(x,y)*g(x,y)-f(x,y)*gy(x,y))/det
        dy = (gx(x,y)*f(x,y)-g(x,y)*fx(x,y))/det
        x = x+dx
        y = y+dy
        err_x = np.abs(dx)
        err_y = np.abs(dy)
        count += 1
        if count>limit:
            raise RuntimeError("count exceeded limit @ newton_method2.")
    return x,y

次の図は, 以上までの関数を用いて Brusselator 方程式に対して固定点におけるヤコビアンの対角和と行列式を計算し, パラメータ $a,b$ を変えつつ tr-det 平面に描画したものです.

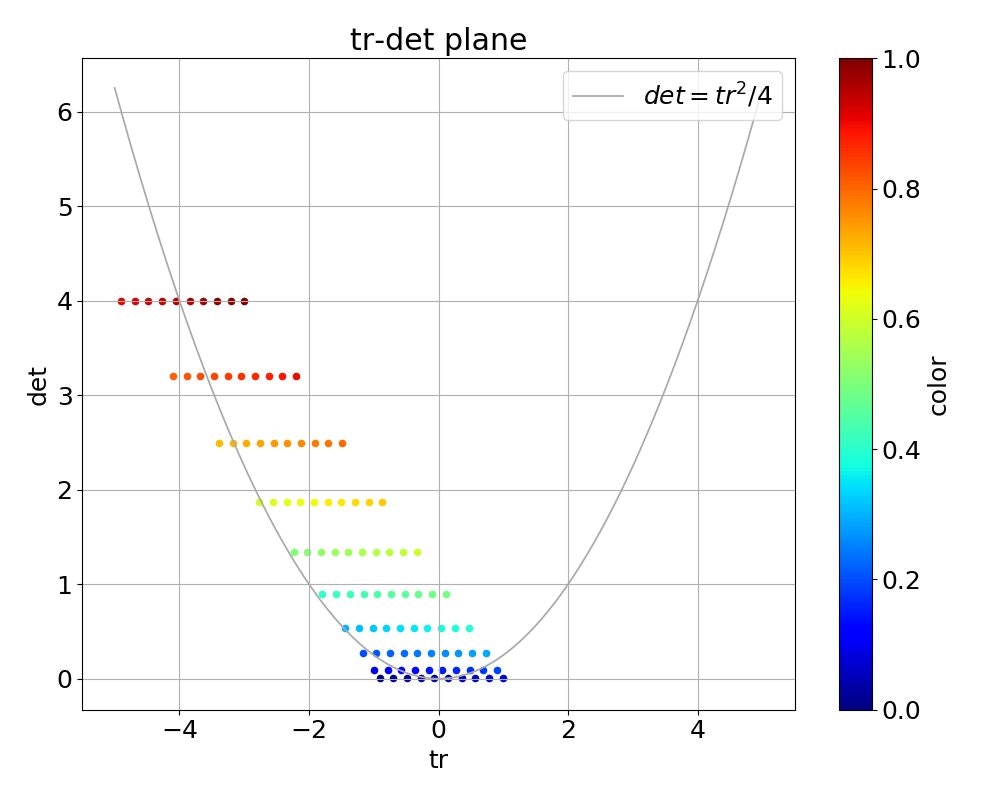
ここで, 上図中の $color$ は次式で計算しています.

\begin{align}
&\hat{a} = \frac{a-a_{min}}{a_{max}-a_{min}},\qquad
\left\{\begin{aligned}
&a\in A=\{a_m\}_{1\le m\le M}\\
&a_{min}=\mathrm{min}\;A\\
&a_{max}=\mathrm{max}\;A
\end{aligned}\right.\\
&\hat{b} = \frac{b-b_{min}}{b_{max}-b_{min}},\qquad
\left\{\begin{aligned}
&b\in B=\{b_n\}_{1\le n\le N}\\
&b_{min}=\mathrm{min}\;B\\
&b_{max}=\mathrm{max}\;B
\end{aligned}\right.\\
&color = \frac{M\hat{a}+\hat{b}}{M+1},\qquad 0\le color\le 1
\end{align}

数値計算では $a_{min}=b_{min}=0.1$, $a_{max}=b_{max}=2$, $M=N=10$ としました.

tr-det 平面を描くだけでは自動微分の恩恵をあまり感じないため, x-y 平面上に固定点を描画してパラメータを変化させた際に固定点の安定性がどうなるかを色で表す gif アニメを最後に掲載します.　gif アニメでは, 固定点の安定性は黒で安定, グレーでセンター, 白で不安定としています.

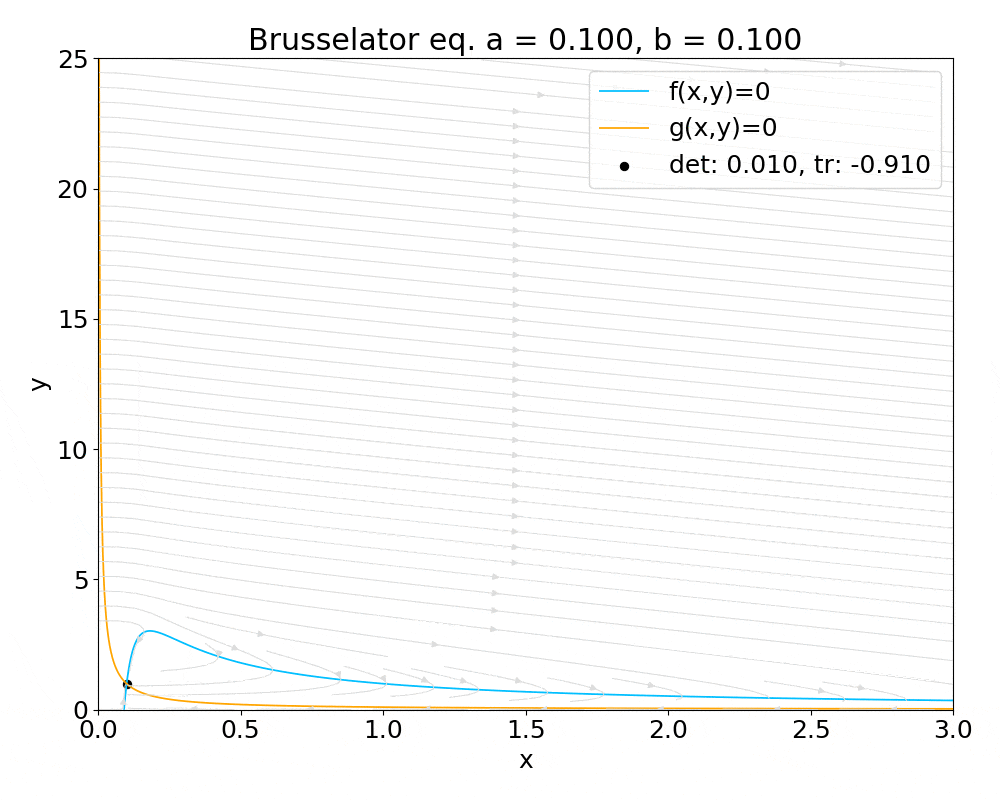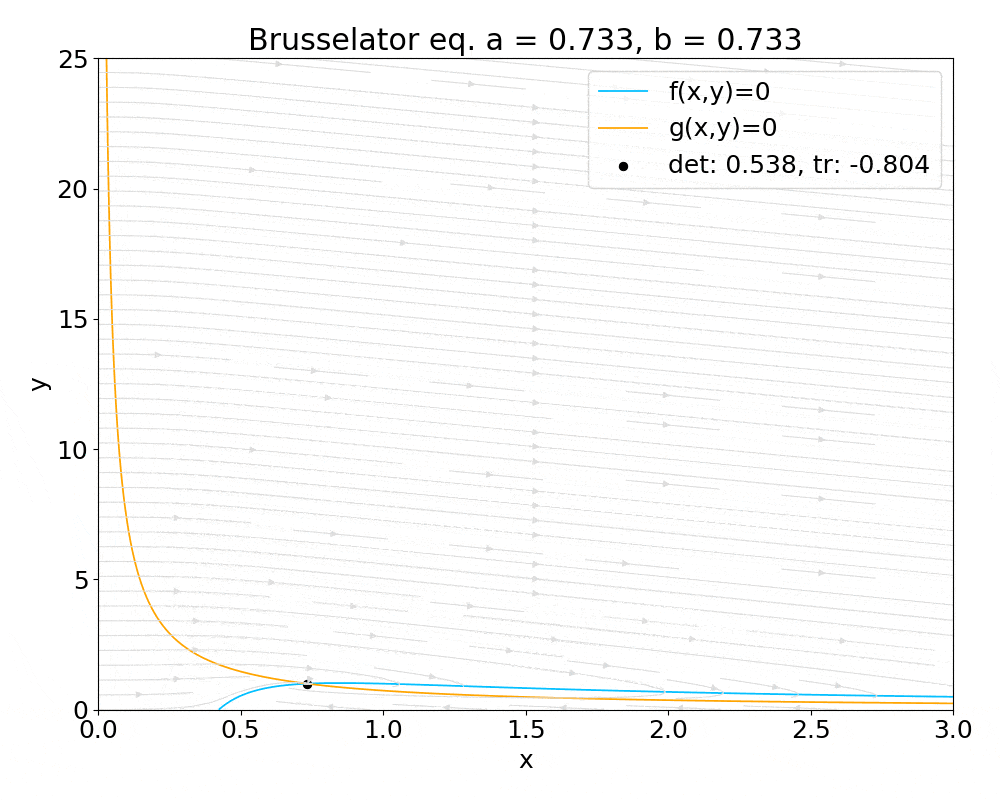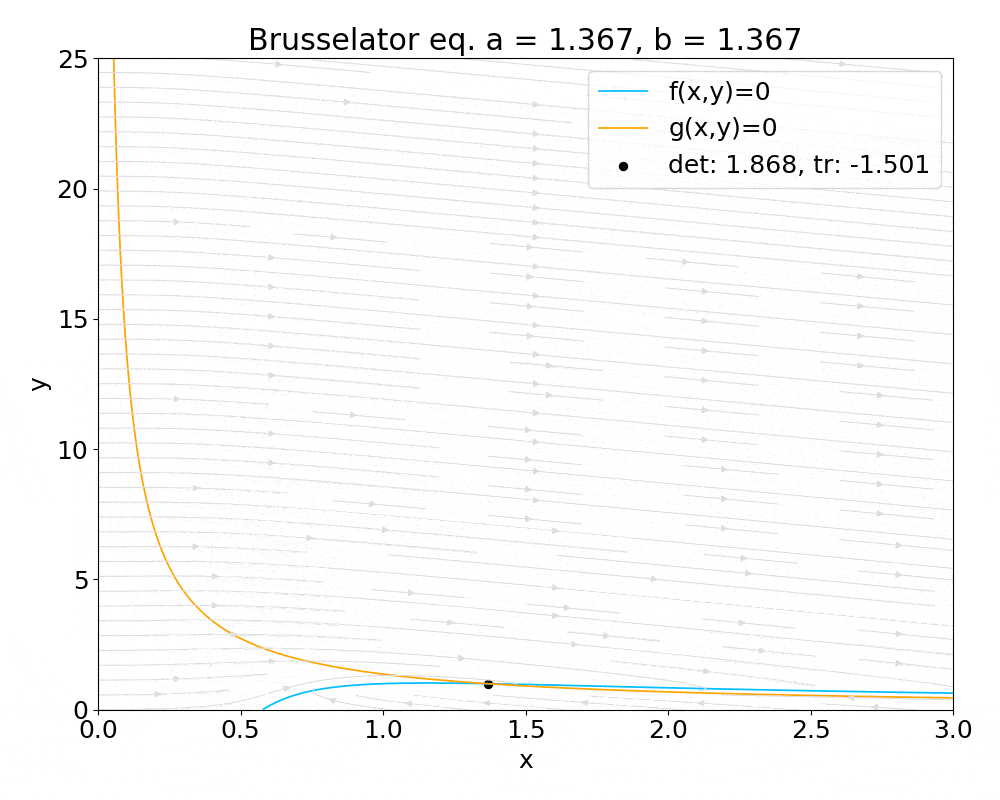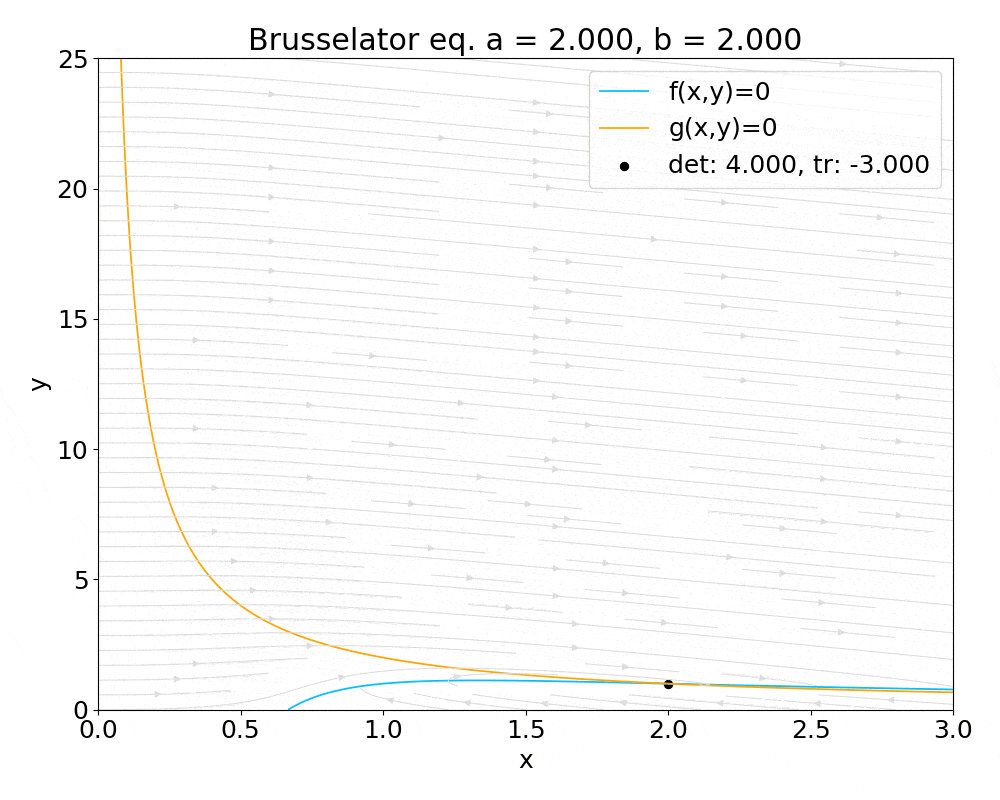
実際に線形安定性解析でdual.pyを利用する場合は、sample2.pyを参考にしてください。