今更強化学習を勉強したっていい

この記事は何か

タイトルの通りです。
強化学習を勉強しようと思ってから長い月日が過ぎたので、書きはじめました。
勉強しながら書くのでだんだん言っていることが変わる可能性があります。
おそらく定性的な議論ばかりして定量的な事をいいません。

なぜ

筆者は趣味で botトレーディング¹ をしています。
結果は鳴かず飛ばずですが、かなり楽しくやっております。
botはよく手入れをしている時は勝てるのですが、すぐに賞味期限が来て高速お金配りシステムへと変貌します。
Qラーニングは、せめて取引の手法がきまっているならその変数調整くらいは自動でやってほしいよねということで、諸々検討しているうちの一つです。

やること

いきなり複雑な系を扱うよりはまずイメージを掴みたかったので下記を題材として進めていきます。

Qラーニングとは

まず人為的に報酬を設定し、適当に初期化した行動規範に従って行動して結果的に得られた報酬をもって行動規範を更新する学習です。
状態-行動 空間の評価値 Q(s,a) を報酬に基づいて計算する手法と言えるかと思います。
系に外乱がなければsにaを作用した結果は確定しているので、sにaを作用した結果をs_aとすると実質Q(s_a) であり盤面を単純に評価しているのに違いなさそうです。

整理

まず前提としてある方針がきまっている(はじめは適当にinit)。
その方針を修正していくのが学習。

名前	表記	説明
状態idx	t	場面を指定するインデックス 関数に与えて返却値を得る
状態	s(t)	状態、至った経緯が行動判断に必要であれば 盤面が同じでも別状態として考えるのが良さそう
行動	a(t)	tのときに取る行動
行動報酬	r(t)	場面tでa(t)を行うことで得られる報酬
累積報酬	R(t)	これから得られることが期待できる報酬合計 ※累積報酬は将来の報酬
割引率	γ	n場面後に起こるgood,badを伝搬する上での重み 0 < γ < 1
行動評価関数	Q(s,a)	状態sにおいてaを選んだときのRを返却する 本来行動指針は決まっているのでs(t)においては指針におけるベストなa(t)しか選ばれないはずだが、例えば別のアクションを取ったときに残りは方針に従った仮定のR'(t)を表していると言えそう

手順

Goでやっていきます。ざっくりと書くと以下になるかと思います。

1. 行動評価関数Q(s,a)を定義する
2. マルバツゲームを作る
3. Q(s,a)を更新する

1. 行動評価関数Q(s,a)を定義する

行動評価関数についておさらいしましょう。
Q(s,a) は場面 s で a_1, a_2, .. を行ったときに期待できる報酬であり、
言い換えれば s における行動 a の評価値となります。
もらえる報酬が高い a を選択した方が勝ちやすいので、s において取れる行動 a_1, a_2, .. をすべて代入した上で一番高い値を出した a が、現状の Agentの最適と思える手となるかと思います。
報酬に関しては下記のように設定します。

結果	報酬値
勝	1
負	-1
引分	0

とりあえず s,a を引数として評価値を返してくれる関数を定義すればよさそう。
func Q(s, a int) float64
一旦最もシンプルに上記で行きます。特徴量がーとか、modelがーとか言う話は今回は対象外です。

s, aの計算に関して

下記のように定義する。
s : null, ○, ✗ の3進数として左上から順に9桁の値を10進数化したものを s
a : 設置:1, それ以外:0 の2進数として左上から順に9桁の値を10進数化したものを a

2. マルバツゲームを作る

参照元²

我々は強化学習を勉強していたはずでは、、
https://github.com/TTRSQ/CircleCrossGame
作りました。
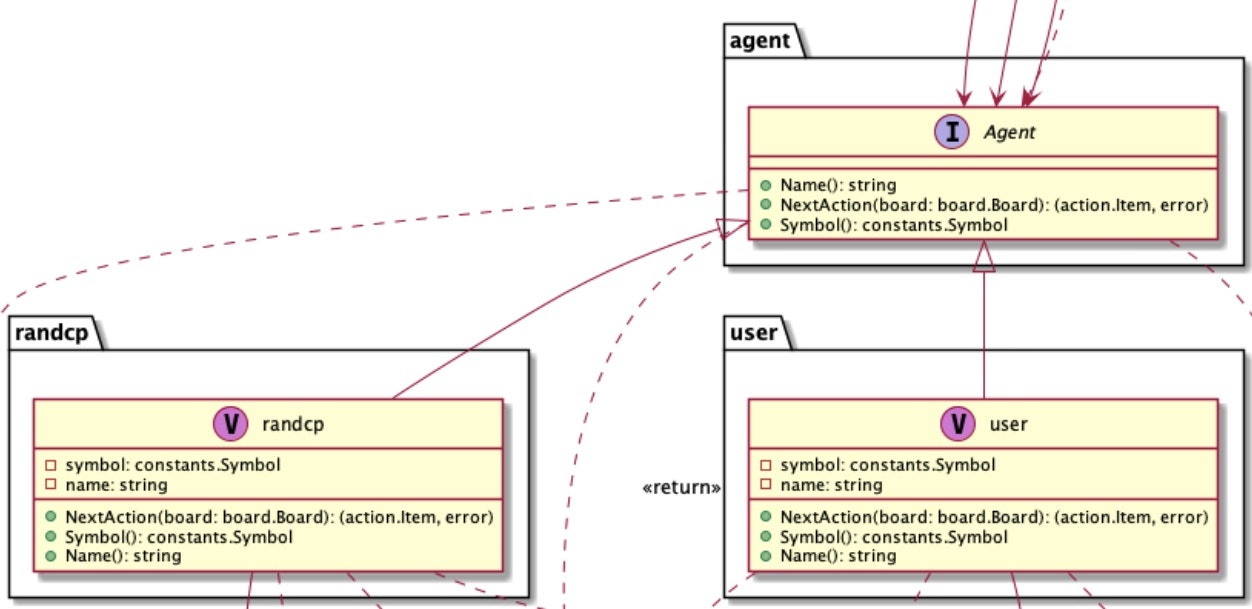
readmeに自動生成したごちゃごちゃしたumlがありますが、今回触るのは下記の部分だけになるかと思います。interface である Agent の具体的な実装として user(手動), randcp(ランダムなcp)があります。

Agent の具体実装として qLearning を実装します

• 盤面を渡されて次のアクションを返す NextAction()
• 固有名を返す Name()
• 自身の担当が ○ か ✗ かを返す Symbol()

この3つを満たしていれば良いので、ここだけ従って後は全部無視していきます。

qLearning.go

type qLearning struct {
	qf      qLearning.qFunc
}

func (q *qLearning) NextAction(board board.Board) (*action.Item, error) {
	stPos := q.calcStatus(board)
	acts := board.CanPutPoints()
	point := -100000.0
	act := []int{}
	for i := range acts {
		actPos := q.calcAct(acts[i][0], acts[i][1])
		pi := q.qf.Value(stPos, actPos)
		// なるべく数値の高いactを選ぶ
		if pi > point {
			point = pi
			act = acts[i]
		}
	}
	return action.NewItem(act[0], act[1], q.symbol)
}

雰囲気上のようになるかと思います。（Name, Symbolは割愛）

3. Q(s,a)を更新する

ゲームを何度もさせながら、勝敗が決まったタイミングで報酬を伝搬させていきます。

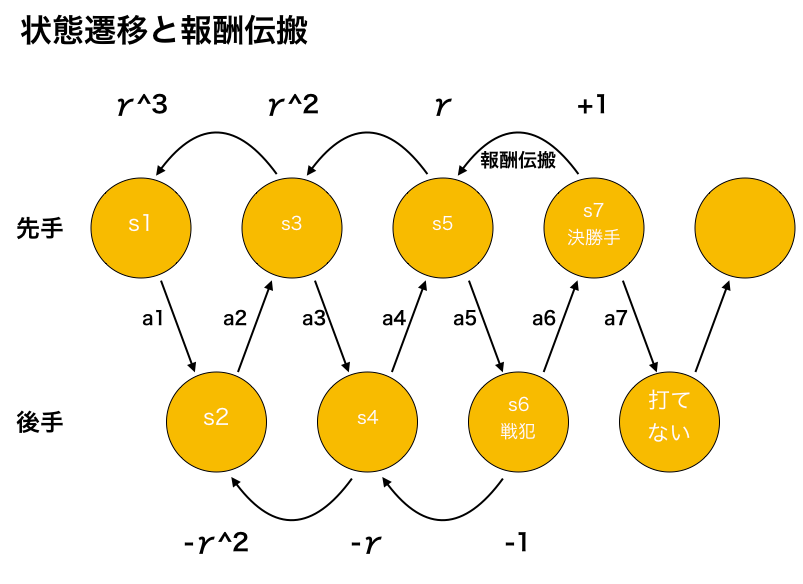
• 1ゲームは先手から始まる最大9ターン
• s1 -> s9 のように状態遷移していく

上記の図では7ターン目に先手が勝利しているので、
Q(s7, a7) に +1 加点
Q(s5, a5) に γ 加点
Q(s3, a3) に γ^2 加点
Q(s1, a1) に γ^3 加点
のようなQ関数の更新が発生します。
同時に負けた方にも遡って加算していきます。
Q(s6, a6) に -1 加点
Q(s4, a4) に -γ 加点
Q(s2, a2) に -γ^2 加点

上記を愚直に実装したものです。
https://github.com/TTRSQ/qLearnAgent
学習中に起こる状態のバリエーションを上げるために1/5の確率で適当に打つように実装しています(ε-greedy)。

結果

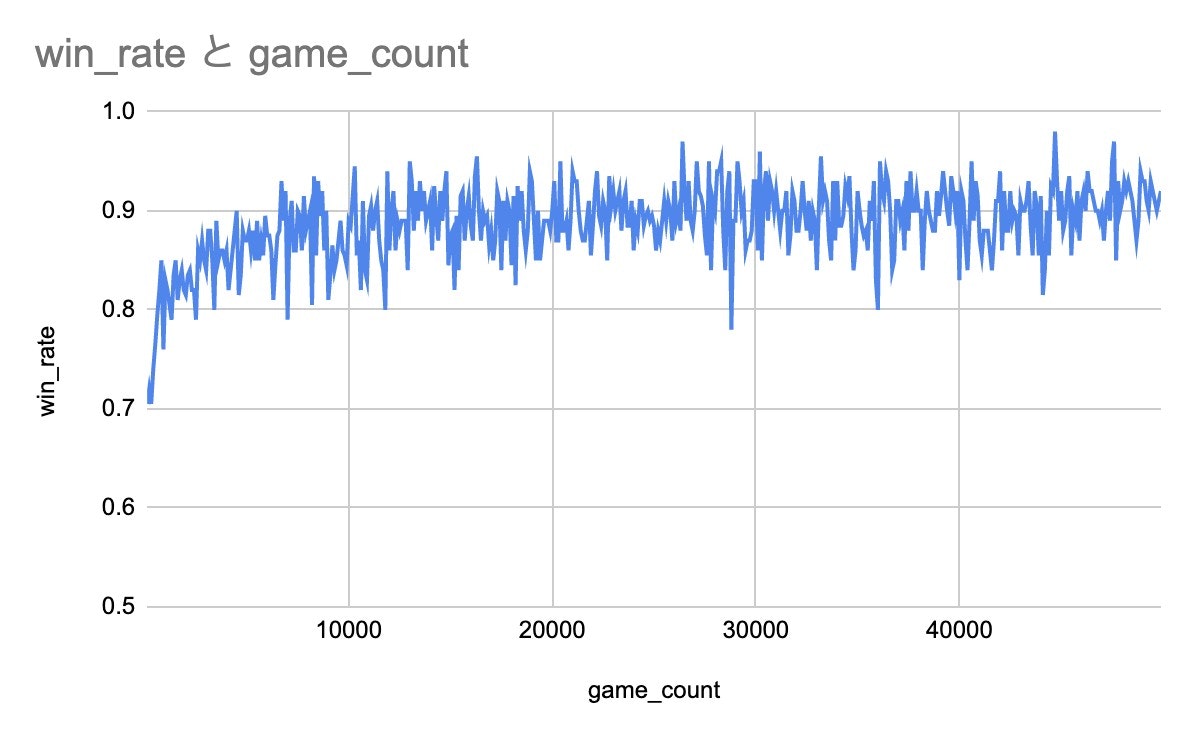上記は5万回学習を行いつつ直近100回の勝率をプロットしたものです。
勝率は90％そこそこで収束しています。20%の確率で適当に打っていることもあり、そんなもんだと思います。

改善

学習初期から終期にかけて、適当に打つ確率を 100% -> 0％ と線形で減らしてみます。

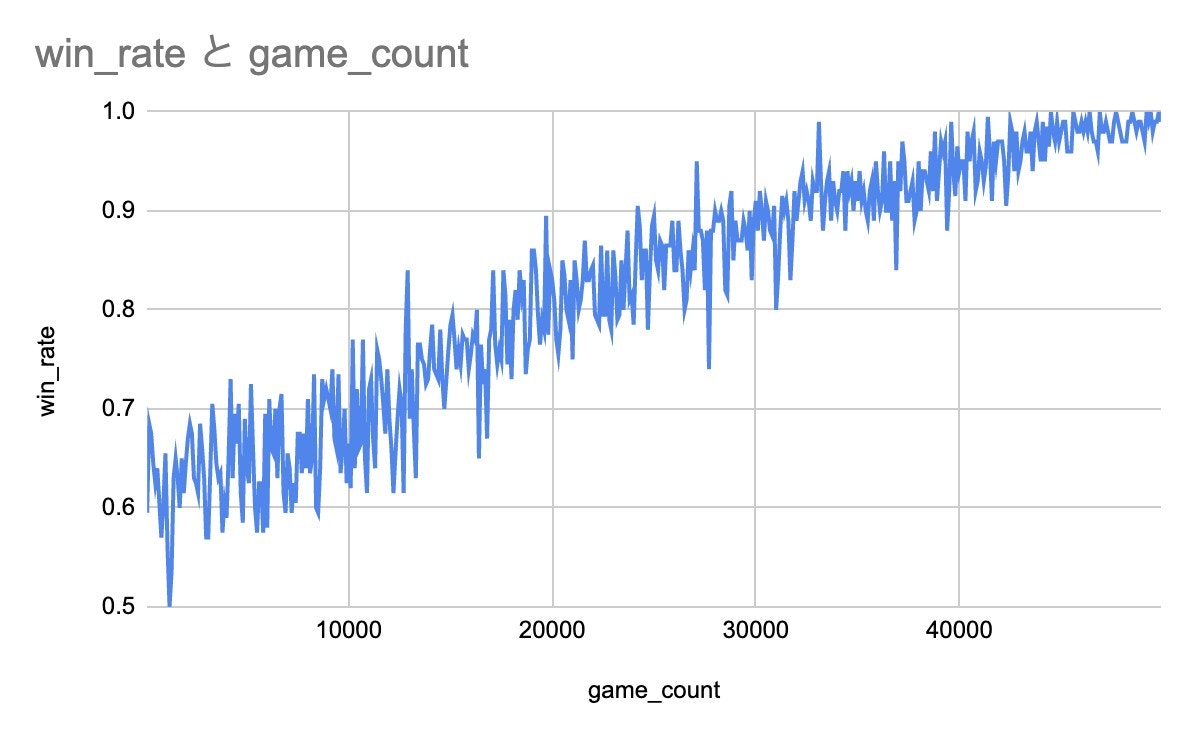
4万ループ目の時点で前者と同じ20％のランダムですが、勝率の改善が見られるように思います。

実際後者は初手で必ず中央に手を設置するようになりました。
どのように学習データを散らすかはかなり重要そうですね。

1. システム連動できる取引所で自動売買するシステム(bot)を運用してお金を得たり失ったりすること。 ↩

2. 『魁!!男塾』第19巻 ↩