この記事はシェーダーアドベントカレンダー Advent Calendar 2019 16日目です。
https://qiita.com/advent-calendar/2019/shader-advent-calender-2019
15日目は@songofsaya_さんの「80年代ゲーセン筐体っぽいレトロ調の画面をUnityシェーダーで作る。」
http://sayachang-bot.hateblo.jp/entry/2019/12/11/231351
でした。
はじめに
フラグメントシェーダによる描画の練習として、フラクタル図形の描画に取り組んだ際の話を書きます。
今回扱うフラクタル図形は
の二つです。
それではやっていきましょう!
フラクタルとは
フラクタルとは、一部が全体に対して相似であるような図形のことをいいます(厳密な定義を筆者は知りませんが、上に挙げたような図形のことです)。
反復関数系
反復関数系とは、フラクタル図形の描画に使われる手法です。
シェルピンスキーのギャスケット
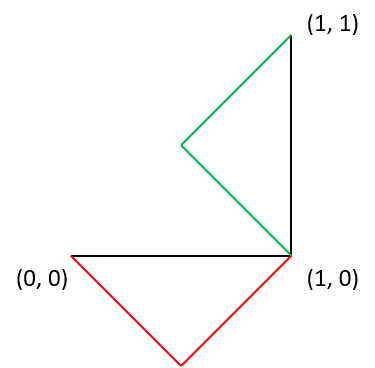
シェルピンスキーのギャスケットでは次の3種類の関数を使います
- 1/2に縮小(下の図の黄色の三角形)
- 1/2に縮小して(1/4, 1/2)平行移動(下の図の赤色の三角形)
- 1/2に縮小して(1/2, 0)平行移動(下の図の緑色の三角形)
これをCanvas2Dで描画するためのJavaScriptコードを次に示します。
const ctx = canvas.getContext('2d');
function f(dot, count) {
if (count == 0) {
ctx.beginPath();
ctx.arc(dot.x * 500, dot.y * 500, 0.5, 0, 2 * Math.PI, true); // キャンバスサイズは500x500の想定
ctx.stroke();
} else {
dot = dot.scale(1 / 2);
f(dot, count - 1);
f(dot.translate(1 / 4, 1 / 2), count - 1);
f(dot.translate(1 / 2, 0), count - 1);
}
}
f(new Dot(0.5, 0.5), 7); // 7回適用させるのでcountに7を指定する
初期点(0.5, 0.5)から初めて、3つの関数のいずれかを7回適用させた後の点をキャンバスに描画しています。7回適用すると、$ 3^7 = 2187 $ 通りの点が描画されます。適用回数を増やすと指数関数的に組み合わせが増加するので注意が必要です。実行結果を下に示します(Canvas2Dでは下方向がy軸プラス方向なので、三角形が下向きになっています)。
ドラゴン曲線
ドラゴン曲線では次の2種類の関数を使います。縮小や平行移動以外に回転操作が含まれます。
- 1/√2に縮小して時計回りにπ/4回転(下の図の赤色の線)
- 1/√2に縮小して時計回りに3π/4回転し、(1, 1)平行移動(下の図の緑色の線)
これをCanvas2Dで描画するためのJavaScriptコードを次に示します。
function f(dot, count) {
if (count == 0) {
ctx.beginPath();
ctx.arc(dot.x * 500, dot.y * 500, 0.5, 0, 2 * Math.PI, true);
ctx.stroke();
} else {
dot = dot.scale(1 / Math.sqrt(2));
f(dot.rotate(- Math.PI / 4), count - 1);
f(dot.rotate(- Math.PI * 3 / 4).translate(1, 1), count - 1);
}
}
f(new Dot(0.5, 0.5), 15);
実行結果
フラグメントシェーダでの実装
上記で示したコードをフラグメントシェーダで表現するとどのようになるでしょうか。
※ 実行環境はWebGL 2.0を想定しています
※ シェーダはGLSL ES 3.0で記述しています
シェルピンスキーのギャスケット
フラグメントシェーダではピクセル単位での処理となります。
知りたいのは、(0.5, 0.5)を対象ピクセルの座標近くに移動させる反復関数の適用順番があるかどうかということです。ここでは、(安直ですが)虱潰し探索を行います。
GLSLでは再帰関数が使えないため、$ 3^{depth} $($depth$は再帰の深さ)までインクリメントし、インクリメントした値を3進数として扱い、3進数の各桁でどの反復関数を使うかを決定します。対象ピクセル座標に対して反復関数の逆操作を行うことで(0.5, 0.5)に近い座標が求まればピクセルを黒で塗ります。
ピクセル毎に、$ depth \times 3^{depth} $回のループが回ることになるので、かなり効率は悪いです。
# version 300 es
precision mediump float;
out vec4 color;
const int depth = 7;
// built-inのpowはfloatを返すので、intを返すpowを自前で用意
int my_pow(int a, int b) {
int _a = a;
for (int i = 0; i < b; i++) {
_a *= a;
}
return _a;
}
void main() {
color = vec4(0.0, 0.0, 0.0, 1.0);
vec2 p = gl_FragCoord.xy / 500.0; // スケールを[0-1]x[0-1]に調整
for (int i = 0; i < my_pow(3, depth); i++) {
int _i = i;
vec2 _p = vec2(p);
for (int j = 0; j < depth; j++) {
int c = _i % 3;
_i /= 3;
switch (c) { // 反復関数の逆操作
case 0:
_p = _p * 2.0;
break;
case 1:
_p = (_p - vec2(0.25, 0.5)) * 2.0;
break;
case 2:
_p = (_p - vec2(0.5, 0.0)) * 2.0;
break;
}
}
if (distance(_p, vec2(0.5)) < 0.5) {
return;
}
}
discard;
}
実行結果を下に示します。
ドラゴン曲線
基本的な部分はシェルピンスキーのギャスケットと同じです。回転操作が必要なので、回転行列を返す関数を追加しています。
# version 300 es
precision mediump float;
out vec4 color;
const int depth = 15;
const float PI = 3.1415926535;
int my_pow(int a, int b) {
int _a = a;
for (int i = 0; i < b; i++) {
_a *= a;
}
return _a;
}
// 回転角に対して回転行列を返す関数
mat2 rotate_matrix(float theta) {
return mat2(
cos(theta), sin(theta),
- sin(theta), cos(theta)
);
}
void main() {
color = vec4(0.0, 0.0, 0.0, 1.0);
vec2 p = gl_FragCoord.xy / 500.0;
mat2 r1_4 = rotate_matrix(PI / 4.0);
mat2 r3_4 = rotate_matrix(PI * 3.0 / 4.0);
for (int i = 0; i < my_pow(2, depth); i++) {
int _i = i;
vec2 _p = vec2(p);
for (int j = 0; j < depth; j++) {
int c = _i % 2;
_i /= 2;
switch (c) {
case 0:
_p = r1_4 * _p * sqrt(2.0);
break;
case 1:
_p = r3_4 * (_p - vec2(1.0)) * sqrt(2.0);
break;
}
}
if (distance(_p, vec2(0.5)) < 0.5) {
return;
}
}
discard;
}
実行結果
負荷軽減
お察しの通り、上記のコードは非常に効率の悪いものとなっています。
(0.5, 0.5)を対象ピクセルの座標近くに移動させる反復関数の適用順番があるかどうか を簡単に求めることができれば、負荷を格段に下げることができます。
シェルピンスキーのギャスケットの場合、次のような書き方をすることでループを$ depth $回だけに削減できます。
# version 300 es
precision mediump float;
out vec4 color;
const int depth = 7;
void main() {
color = vec4(0.0, 0.0, 0.0, 1.0);
vec2 p = gl_FragCoord.xy / 500.0;
// 余計なところに色を塗らない
if (dot(p, vec2(1.0, 0.5)) > 1.0 ||
dot(p, vec2(0.0, -1.0)) > 0.0 ||
dot(p, vec2(-1.0, 0.5)) > 0.0) {
discard;
return;
}
for (int i = 0; i < depth; i++) {
// ここの条件で、反復関数を選択する
if (dot(p, vec2(1.0, 0.5)) < 0.5) {
p *= 2.0;
} else if (dot(p, vec2(0.0, -1.0)) < -0.5) {
p = (p - vec2(0.25, 0.5)) * 2.0;
} else if (dot(p, vec2(-1.0, 0.5)) < -0.5) {
p = (p - vec2(0.5, 0.0)) * 2.0;
} else {
discard;
return;
}
}
}
実行結果
まとめ
- フラグメントシェーダでもフラクタル図形を描画できた
- ここで紹介したやり方だと負荷が大きい
- シェルピンスキーのギャスケットなどの一部の図形はフラグメントシェーダで効率よく描画できる
- ソースコード置き場: https://github.com/ttk1/sac-2019
誰かドラゴン曲線を効率よく描画する方法を教えてください。
17日目は@songofsaya_さんの「ノイズについて書きたい。」の予定です。