この記事の目的
この記事の目的
**焼きなまし法(Simulated Annealing:シミュレーテッド・アニーリング)**を応用し、組合せ最適化問題の代表的な問題の一つの巡回セールスマン問題を解きます。
さらに、計算モデルとしてボルツマンマシンモデルを採用し、Pythonでプログラミングを行い、最適解を求めます。
 焼きなまし法の理論について
焼きなまし法の理論について
ここで取り上げる焼きなまし法に関する数式や基本理論については、下部「出典」に記載の参考書「最適化アルゴリズム」(P120~)に詳細の説明がありますので、ここでは割愛させて頂きます。
主にプログラミングを中心に記事にしたいと思います。
 簡単な巡回セールスマン問題
簡単な巡回セールスマン問題
巡回セールスマン問題として、こちらで取り組んだ問題と同じ問題を使用します。
■遺伝的アルゴリズム(GA)とそのライブラリ(vcopt)で巡回セールスマン問題を解く
https://qiita.com/ttlabo/items/9b00a29702d1205f6996
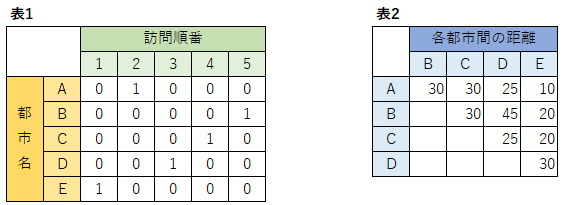
以下のような、各行が都市名、各列が訪問の順番を示す表1を考えます。
ある順番である都市を訪れる場合は表の値が1、訪れない場合は値が0となります。
例えば表1では、巡回する順番は、都市E→都市A→都市D→都市C→都市B→都市Eとなります(最後は出発した都市に戻ります)。
また、表2に各都市間の距離を定義します。
これらの5都市を回る(対称型)巡回セールスマン問題(TSP:Travelling Salesman Problem)にボルツマンマシンモデルを適用して問題を解きます。
 目的関数のエネルギー式(ハミルトニアン)の立式
目的関数のエネルギー式(ハミルトニアン)の立式
参考書から引用すると、焼きなまし法の基本的な考え方は以下と定義されます。
焼きなまし法の基本的な考え方
目的関数$f(x)$: 系のエネルギー(ハミルトニアン)
$f(x)$の変数$x$: ある確率分布に従って変化する系の状態
温度パラメータ$T$: 状態遷移確率を制御する変数上記について、温度パラメータ$T$を高い値から低い値に徐々に変化させる
ことによって$f(x)$の安定点(最小値)を探索する。
ここで、目的関数であるハミルトニアンを定義する必要があります。
ハミルトニアンは、その値が最小になったときに最適解が求まるように工夫して立式します。
例えば、問題を解く際に相応しくない経路や違反条件を取ったときにハミルトニアンの値が大きくなるような項を追加します。この項をペナルティ項と呼びます。
今回の問題では、ハミルトニアン$H$として以下を考えます。
\begin{eqnarray}
ハミルトニアン H &=& H_A + H_B\\
H_A &=& 各都市間の距離を求める項\\
H_B &=& ペナルティ項
\end{eqnarray}
まず、$H_A$について考えます。都市$i$、都市$j$の距離を$d_{i,j}$とし、変数$x$を表1の各マスに合てはめ、$x_{i,k}$とします。ここで、$x_{i,k}$は都市$i$に対して$k$番目に訪問するかどうかを決定する変数です。訪問するなら1、訪問しないなら0をとる変数で、バイナリー変数と呼びます。
航路の合計は、都市$i$を$k$番目に訪れ、都市$j$を$k+1$番目に訪れた際の距離$d_{i,j}$を順番に加算して行けば良いので、$H_A$を以下のように定義します。
H_A = K_1\sum_{i=1}^{5}\sum_{j=1}^{5}\sum_{k=1}^{5}d_{i,j}x_{i,k}x_{j,k+1} … 式(1)
上式で$K_1$は定数とします。
3番目の$\sum$(シグマ記号)における$k$の取る範囲について注意が必要です。$k$=5の時、シグマ計算の対象となる$x$は$x_{i,5}x_{j,6}$となり、6番目に訪問する都市が必要になります。本問題では、最初に訪問した都市(1番目)に戻ることとします。
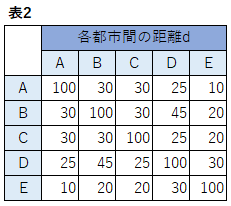
ここで、同じ都市を続けて訪れることができないので、$d_{i,i}$の値を大きく設定して、$H_A$の値が大きくなることで解として選択されないようペナルティを付与します。つまり、$d_{1,1}$,$d_{2,2}$,,,$d_{5,5}$についても値を設定します。また、表2の左下の空白部分についても都市間の組み合わせを考え距離を設定します。対称行列のように設定すれば良いです。よって、表2を以下のように再定義します。
次に、$H_B$について考えます。
表1について、それぞれの行、列ごとに含まれる1の数は1個、0の数が4個です。
これは同じ都市を複数回訪問したり、同時に複数の都市を同じ訪問順番で訪れることがないということになります。
つまり、各行、各列ごとの和は必ず1となります。もし1でない場合は値が大きくなるペナルティ項として考えればよく、$H_B$を以下とします。
H_B = K_2\Biggl[\sum_{i=1}^{5}\bigg(\sum_{k=1}^{5}x_{i,k}-1\bigg)^2 + \sum_{k=1}^{5}\bigg(\sum_{i=1}^{5}x_{i,k}-1\bigg)^2\Biggl] … 式(2)
上式で、$K_2$についても定数とします。
$H_A$と$H_B$を定義しましたので、ハミルトニアン$H$は以下となります。
H = K_1\sum_{i=1}^{5}\sum_{j=1}^{5}\sum_{k=1}^{5}d_{i,j}x_{i,k}x_{j,k+1} + K_2\Biggl[\sum_{i=1}^{5}\bigg(\sum_{k=1}^{5}x_{i,k}-1\bigg)^2 + \sum_{k=1}^{5}\bigg(\sum_{i=1}^{5}x_{i,k}-1\bigg)^2\Biggl] … 式(3)
 プログラムのアルゴリズムを考える
プログラムのアルゴリズムを考える
参考書をもとにしてアルゴリズムを作成していきます。
まず、ボルツマンマシンモデルの根幹となる以下の論理式を考えます。
以下の式はギブス・ボルツマン分布と呼ばれ、物理学(統計力学)において、温度と気体などの粒子系の振る舞いを記述する式です。$f(x)$は系のエネルギー、$T$は温度に相当するパラメータです。
g(x,T) = \frac{1}{\sum_{x}^{}exp\big(\frac{-f(x)}{T}\big)}exp\big(\frac{-f(x)}{T}\big) … 式(4)
ボルツマンマシンモデルの計算では、温度$T$を0に近づけていきます。
温度を0に近づけることで、マルコフ連鎖のエルゴード定理(参考書P123)により一つの平衡状態分布に近づけることができ、最適解が求まります。
ここで、上記の温度$T$について以下のように時刻$t$の関数として定義します。温度を下げる代わりに$t$を変化させて計算を行います。
T(t) = \frac{k}{ln(t+2)} … 式(5)\\
(t=0,1,2,...)
上式で$k$は定数、$ln$は自然対数です。
温度Tを下げるごとに系のエネルギー(ハミルトニアン)が変化しますので、このエネルギーが変化した際に、その変化を取り入れるかどうかを判定する指標を設定します。
この指標は受理確率と呼ばれます。受理確率は、ギブス・ボルツマン分布の式(4)と以下の受理関数$F_B$から、以下の式ように導きます(参考書P129)。
ここで、$A(x,y)$を受理確率、$E(x)$または$E(y)$は系のエネルギー(ハミルトニアン)、$g(x,T)$はギブス・ボルツマン分布式とします。$x$はエネルギーの変化前の状態、$y$はエネルギーの変化後の状態です。
受理確率 A(x,y) = F_B\bigg(\frac{g(y,T)}{g(x,T)}\bigg)\\
= \frac{1}{1+exp\big(\frac{E(y)-E(x)}{T}\big)} … 式(6)\\
受理関数 F_B(s) = \frac{s}{1+s}
必要な式が揃いましたので、アルゴリズムを構築します。
プログラムの初期条件を考えます。
時刻$t$は上記の通り、0から始まり、インクリメントして1ずつ大きくしていきます。インクリメントはループ処理の中で行うとし、ループ回数をloopとします。$t$は0からloop-1まで変化します。
2次元配列型変数$x$の初期状態を考えます(Pythonプログラム上はdict型としています)。
$x$はそれぞれの都市を訪問するかしないか決める変数で、決定変数と呼びます。
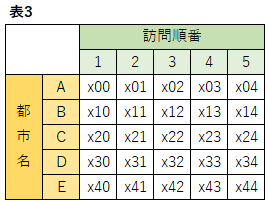
0または1を取るバイナリー変数であり、今回は下図のように5x5の2次元配列と考えます(インデックス番号を0始まりとしています)。
この決定変数配列$x$を初期化します。初期化の方法は、0または1をランダムに設定するようにします。
初期化処理後、ループ処理を開始します。
このループ処理は温度を下げることに相当します。
ループの回数は変数loopで保持させますが、具体的な回数に決まりはありません。プログラムの動作状況により決めます。
まず、温度$T$を取得します。温度$T$は式(5)で決定します。
決定変数$x$の中からランダムに一つを選択します。
$x$は5x5行列の2次元配列なので、x方向y方向にそれぞれランダムな座標$(i,j)$を取得します。
ランダムに取得した$x(i,j)$の値を反転させます。反転するとは、$x(i,j)$の値が1なら0に、0なら1に変えることです。
この$x(i,j)$を反転させることを「状態を変化させる」と言います。
状態を変化させたときに系のエネルギー(ハミルトニアン)がその前後でどう変化するかを計算し、その変化を取り入れるかどうかを判断します。
本プログラムでは、状態を変化させた2次元配列を$y$として新規に確保します。
この変化を取り入れるかどうかを決める確率を受理確率と呼びます(参考書P128)。受理確率は式(6)で算出します。変化前の状態(系のエネルギー)が$E(x)$、変化後の状態が$E(y)$です。系のエネルギー(ハミルトニアン)は式(3)で計算します。
上記の変化について受理確率がある閾値を超えたら受理し、超えない場合は受理しないとします。受理するとは、ランダムに選択した$x(i,j)$の値の反転を受け入れること、受理しないとは$x(i,j)$の値をそのままにするという意味です。
プログラムでは、閾値をjuri_hanteiという変数で設定します。また、受理する場合は、2次元配列$y$を$x$に移し替えます。
受理確率により変化後の状態の設定をしたら、時刻を一つ先に$t=t+1$として進めます。
上記のループを繰り返します。
ループが終了した時点での$x$が最終的な解となります。
 アルゴリズムの整理
アルゴリズムの整理
上述のアルゴリズムを下図のように手続き順に整理しました。
1. 変数の定義
ループ回数をloop=50000とする。
都市間の距離di,jを定義する。
ハミルトニアンの定数K1,K2を定義する。
温度を決めるための定数k(式5)を定義する。
k1,k2及びkの値はプログラムの動きを見ながら決定する。
受理確率による受理判定の閾値juri_hanteiを定義する。
juri_hanteiの値はプログラムの動きを見ながら決定する。
2. 初期化
時刻t=0とする。
変数x(2次元配列)の各要素に0または1をランダムに設定する。
プログラムで使用する関数を定義する。
3. ループ処理開始
式(5)より温度Tpを取得する。
ランダムにx[i,j]を選択する。1次元(y軸)方向i、2次元(x軸)方向jそれぞれで
ランダムに特定してx[i,j]を選択する。
xと同じ要素数(次元数)でx[i,j]の値のみが反転(0ならば1、1ならば0)し、
その他の値はxと同じである2次元配列yを作成する。
受理確率(式6)を算出する。
受理確率が閾値を超えた場合、xにyを代入する。(そうでないならxはそのままで何もしない)
t=t+1とする。
ループの開始位置に戻る。
4. 結果取得
最終的に得られたxを最適解として画面に表示する。
総距離を計算して画面に表示する。
 プログラムの実装
プログラムの実装
今回のプログラミングは以下としました。
import random
import math
# =====================================================================
# 1. 定数定義
# =====================================================================
# ループ回数
loop = 50000
# 距離の定義
d = [
[100, 30, 30, 25, 10],
[ 30, 100, 30, 45, 20],
[ 30, 30, 100, 25, 20],
[ 25, 45, 25, 100, 30],
[ 10, 20, 20, 30, 100]
]
# 2次元配列xの1次元(y方向)の要素数
len_x_y = 5
# 2次元配列xの2次元(x方向)の要素数
len_x_x = 5
# ハミルトニアンの定数
k1 = 0.01
k2 = 1
# 温度を決めるための定数
k = 5
# 受理確率により受理するかどうかを判定する閾値
juri_hantei = 0.05
# =====================================================================
# 2. 初期化
# =====================================================================
# 時刻の初期化
t = 0
# 2次元配列の要素について、ランダムに0,1を設定する
x = {}
for i in range(len_x_y):
for j in range(len_x_x):
x[i,j] = random.randint(0,1)
# =====================================================================
# 関数定義
# =====================================================================
# ハミルトニアン
def H(x):
HA = 0
sumA = 0
sumB = 0
for i in range(len_x_y):
for j in range(len_x_y):
for k in range(len_x_x):
k_from = k
if k == len_x_x - 1:
k_to = 0
else:
k_to = k + 1
sumA += d[i][j] * x[i,k_from] * x[j, k_to]
HA += k1 * sumA
sumB1 = 0
for i in range(len_x_y):
for k in range(len_x_x):
sumB1 += x[i,k]
sumB += sumB1 * sumB1
sumB1 = 0
sumB2 = 0
for i in range(len_x_y):
for k in range(len_x_x):
sumB2 += x[i,k]
sumB -= 2 * sumB2
sumB2 = 0
for i in range(len_x_y):
sumB += 1
sumB3 = 0
for k in range(len_x_x):
for i in range(len_x_y):
sumB3 += x[i,k]
sumB += sumB3 * sumB3
sumB3 = 0
sumB4 = 0
for k in range(len_x_x):
for i in range(len_x_y):
sumB4 += x[i,k]
sumB -= 2 * sumB4
sumB4 = 0
for k in range(len_x_x):
sumB += 1
HA += k2 * sumB
return HA
# 温度関数の定義
def T(t):
T = k / math.log(t + 2)
return T
# 受理確率の算出
def A(x,y,T):
tmp = H(y) - H(x)
A = 1 / (1 + math.exp(tmp / T))
return A
# =====================================================================
# 3. ループ処理
# =====================================================================
while t < loop:
# 温度を取得する
Tp = T(t)
# 2次元配列xからランダムに一つを選択する(ランダムな座標i,jの取得)
r_i = random.randint(0,len_x_x - 1)
r_j = random.randint(0,len_x_x - 1)
# ランダムに一つ選択した座標のみ反転させた、状態yの2次元配列yを作成する。
y = {}
for i in range(len_x_y):
for j in range(len_x_x):
if i == r_i and j == r_j:
# 反転する
y[i,j] = -1 * (x[i,j] - 1)
else:
y[i,j] = x[i,j]
# 受理確率を算出
juri = round(A(x,y,Tp), 2)
# 時刻変数と受理確率を表示
print('t=',t,'juri=',juri)
# 受理確率により受理するかどうかを判定する
if juri >= juri_hantei:
x = y
print('▼受理しました。')
# 時刻tを進める
t = t + 1
# =====================================================================
# 4. 結果表示(訪問都市)
# =====================================================================
print('----- 結果表示 -------')
for i in range(len_x_y):
line = ''
for j in range(len_x_x):
line += ' '
if x[i,j] == 1:
line += 'o'
else:
line += '-'
print(line)
# =====================================================================
# 5. 結果表示(総距離)
# =====================================================================
# 訪問する都市を保持するリスト
city = []
for k in range(len_x_x):
for i in range(len_x_y):
if x[i,k] == 1:
city.append(i)
# 最後に訪問した都市から最初に訪問した都市へ帰還する経路を追加する
city.append(city[0])
# 総距離を計算する
td = 0
for c in range(len(city) - 1):
td += d[city[c]][city[c+1]]
print('total distance:', td)
 実行結果の検証
実行結果の検証
焼きなまし法(Simulated Annealing:シミュレーテッド・アニーリング)で得られる解は近似解であり、厳密解ではありません。反復して計算を行い最終的により良い解を決定します。この解を最適解と呼びます。
よって、反復回数などにより得られる最適解が毎回多少異なることがあります。
反復計算を何度か行い、最も良く出現する解を最終的な最適解として結論します。
今回の最適解は以下でした。
都市の巡回順を都市Eを始点としてE→A→D→C→B→Eと回れば良いことがわかりました。ちなみに、都市Aを始点にするとA→D→C→B→E→Aとなります。
総距離は110です。
特に今回苦労した点は、ハミルトニアンに関する変数k1とk2、温度に関する変数k、閾値juri_hanteiの決定でした。
k1とk2の大小関係を上手く調整しないとペナルティ項が有効に働かず、巡回経路が重複したり、訪問都市数が少ない解が出ました。
温度に関する変数kをちょうど良い値に設定しないとexp関数の処理でオーバーフローが出たり、受理確率が小さすぎて判定できない事象が出ました。
閾値juri_hanteiをちょうど良い値にすることで、ループ処理50000回のうち前半は状態変化を受理する回数が多く、後半はハミルトニアンが収束したため受理する回数が少なくなるように処理のシナリオを理想的な形に収めることができました。
終わり
 出典
出典
 関連情報
関連情報
■Blueqatで簡単な頂点被覆問題を解く
https://qiita.com/ttlabo/items/b4ab222ef9c5ee99233c
■Blueqatでナップサック問題を解く一例
https://qiita.com/ttlabo/items/537564c90056a6d56879
■遺伝的アルゴリズム(GA)とそのライブラリ(vcopt)で巡回セールスマン問題を解く
https://qiita.com/ttlabo/items/9b00a29702d1205f6996
■GoogleのOR-Toolsでナップサック問題を解く - 組合せ最適化問題の基礎を実践
https://qiita.com/ttlabo/items/bcadc03004418f32f49d
■[第1回] 最適化とは? - 数理最適化を学ぶ勉強資料
https://qiita.com/ttlabo/items/e6970c6e85cce9ff4e34
 ご意見など
ご意見など
ご意見、間違い訂正などございましたらお寄せ下さい。