機械学習で使用する評価関数のまとめ

この記事の目的

機械学習では、入手したデータを評価したり、これらのデータを元に算出した予測値の良し悪しを評価する際に、何らかの関数を用いて評価を行います。
評価のための関数は評価関数と呼ばれ、それぞれのケースに相応しい評価関数が用いられます。
この記事では、これらの様々な評価関数を詳しく学ぶとともに、どのようなケースに用いられるかも確認します。

機械学習の種類

評価関数を学ぶ前に、まず機械学習にはどのような種類があるかを確認します。
これらの種類に応じて評価関数も使い分けが行われます。

ここでは主に以下のような種類を取り扱います。
　(1)回帰
　(2)二値分類
　　(2-1)混同行列を用いた二値分類
　　(2-2)確率を予測値とする二値分類
　(3)多クラス分類(マルチクラス分類)

(1)回帰で使用される評価関数

RMSE(二乗平均平方根誤差)

　RMSE：Root Mean Squared Error
　評価関数の値(誤差)をE(x)とすると、

E(x) = \sqrt{\frac{1}{n}\sum_{i=1}^{n}(x_i-\hat{x_i})^2}\\
n：データ数\\
x_i：i番目の実測値(正解値)\\
\hat{x_i}：i番目の予測値

<解説>
　・回帰タスクで最もよく使用される評価関数
　・正解値と予測値の差の二乗和平均の平方根を取ったもの
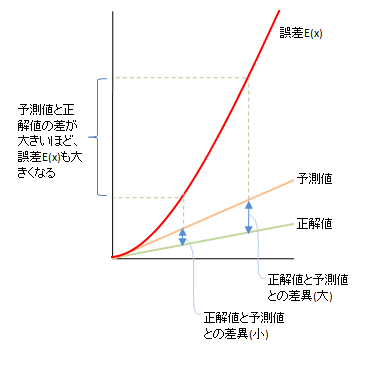
　・予測値と正解値の差の二乗を取るため、その差が大きいほど誤差E(x)に大きな
　　影響を与える(図1)
　・外れ値が誤差E(x)の値を大きく引っ張るため、なるべく除外しておく

図1
　予測値と正解値の差が大きいほど、誤差E(x)も大きくなる

Python関数

　Pythonのscikit-learnライブラリでのRMSE関数の使用方法

RMSE関数

sklearn.metrics.mean_squared_error(x_true, x_pred, sample_weight=None, multioutput='uniform_average', squared=True)
# x_true：正解値のデータ
# x_pred：予測値のデータ
# 3番目以降のパラメータは省略可

RMSLE(二乗平均平方根対数誤差)

　RMSLE：Root Mean Squared Logarithmic Error
　評価関数の値(誤差)をE(x)とすると、

E(x) = \sqrt{\frac{1}{n} \Big\{ \log (1+x_i) - \log (1+\hat{x_i}) \Big\}^2}\\
n：データ数\\
x_i：i番目の実測値(正解値)\\
\hat{x_i}：i番目の予測値

<解説>
　・回帰タスクの代表的な評価関数
　・正解値と予測値の対数差の二乗和平均の平方根を取ったもの
　・予測値が正解値より小さい場合、誤差E(x)に大きな影響を与える
　・予測値が正解値より小さく、さらにその差が大きくなるほど、誤差E(x)の値を
　　大きく引っ張る(図2)

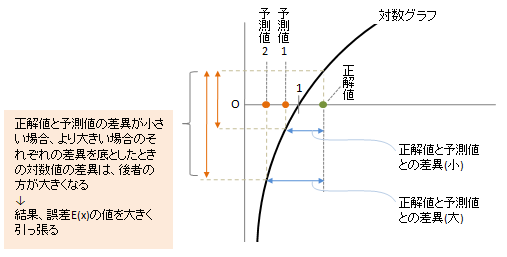
図2
　予測値が正解値より小さく、さらにその差が大きくなるほど、誤差E(x)の値を大きく引っ張る
　→対数グラフの特徴から、グラフが左に近づくほど(xが0に近づくほど)y軸下方向に大きく下がるため

Python関数

　Pythonのscikit-learnライブラリでのRMSLE関数の使用方法

RMSLE関数

sklearn.metrics.mean_squared_log_error(x_true, x_pred, sample_weight=None, multioutput='uniform_average')
# x_true：正解値のデータ
# x_pred：予測値のデータ
# 3番目以降のパラメータは省略可

MAE(平均絶対誤差)

　MAE：Mean Absolute Error
　評価関数の値(誤差)をE(x)とすると、

E(x) = \frac{1}{n}\sum_{i=1}^{n}|x_i - \hat{x_i}|\\
n：データ数\\
x_i：i番目の実測値(正解値)\\
\hat{x_i}：i番目の予測値

<解説>
　・回帰タスクでよく使用される評価関数
　・正解値と予測値の差を二乗しないため、差にばらつきがあっても比較に利用しやすい
　・上記の理由から、外れ値の影響は比較的小さい

Python関数

　Pythonのscikit-learnライブラリでのMAE関数の使用方法

MAE関数

sklearn.metrics.mean_absolute_error(x_true, x_pred, sample_weight=None, multioutput='uniform_average')
# x_true：正解値のデータ
# x_pred：予測値のデータ
# 3番目以降のパラメータは省略可

決定変数

　決定変数$R^2$は以下のように定義されます。

R^2 = 1 - \frac{\sum_{i=1}^{n}(x_i-\hat{x_i})^2}{\sum_{i=1}^{n}(x_i-\bar{x})^2}\\
n：データ数\\
x_i：i番目の実測値(正解値)\\
\hat{x_i}：i番目の予測値\\
\bar{x}：正解値の平均

<解説>
　・回帰分析の当てはまりの良し悪しを確認する指標値
　・値が1に近いほど予測精度が高い(最大値は1)
　・分母は平均値との差で、偏差を意味する
　・分子はRMSEと同様の計算内容であり、その値(誤差)が小さいほど良い
　・分子の値が小さいほど、$R^2$は1に近づく

Python関数

　Pythonのscikit-learnライブラリでの決定変数$R^2$の使用方法

R2関数

sklearn.metrics.r2_score(x_true, x_pred, sample_weight=None, multioutput='uniform_average')
# x_true：正解値のデータ
# x_pred：予測値のデータ
# 3番目以降のパラメータは省略可

(2-1)混同行列を用いた二値分類の評価関数

まずは混同行列について確認します。

混同行列とは、モデルが予測した二値分類の結果を正解データと突き合わせて結果を評価する真理表です。
この表は以下のように4つの領域に分けられ、それぞれ領域(状態)は真陽性(True Positive)、偽陰性(False Negative)、偽陽性(False Positive)、真陰性(True Negative)と呼ばれます。

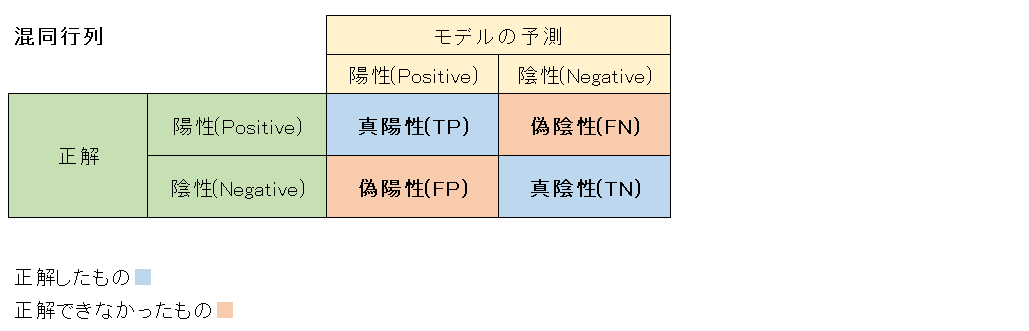
4つの領域のそれぞれの意味について、参考書(本記事下部の出典参照)では以下のように書かれています。

　・ネコを正しくネコと推測できている状態：真陽性(TP)
　・ネコではないものを正しくネコではないと推測できている状態：真陰性(TN)
　・イヌを誤ってネコと推測している状態：偽陽性(FP)
　・ネコを誤ってイヌと推測している状態：偽陰性(FN)

ここで、「真／偽」や「陽／陰」などそれぞれの状態(言葉)の意味を見てみましょう。

真／偽、陽／陰	意味
真	推測結果が正解したことを意味します。
偽	推測結果が不正解したことを意味します。
陽	モデルが当たりと推測したものを意味します。平たく言うと「分類したところ、これは当たりだろう」とモデルが判断したものです。
陰	モデルが外れと推測したものを意味します。平たく言うと「分類したところ、これは違うだろう」とモデルが判断したものです。

正解率と誤答率

　正解率(Accuracy)、誤答率(Error Rate)は以下のように定義されます。

Accuracy = \frac{TP+TN}{TP+TN+FP+FN}\\
Error Rate = 1 - Accuracy

<解説>
　・正解率、誤答率が単独で使用されることはあまりありません。

Python関数

　Pythonのscikit-learnライブラリでのAccuracyの使用方法

Accuracy関数

sklearn.metrics.accuracy_score(x_true, x_pred, normalize=True, sample_weight=None)
# x_true：正解値のデータ
# x_pred：予測値のデータ
# 3番目以降のパラメータは省略可

適合率(精度)と再現率

　**適合率(または精度：Precision)**は以下のように定義されます。

Precision = \frac{TP}{TP+FP}

<解説>
　・陽性(Positive)と予測されたデータのうち、実際に陽性(Positive)だったデータの割合を
　　示す指標
　・モデルが当たりと判断したもののうち、本当に当たりだった割合
　・適合率と精度(Precision)は同じ

　**再現率(Recall)**は以下のように定義されます。

Recall = \frac{TP}{TP+FN}

<解説>
　・実際の陽性(Positive)データのうち、モデルが正解することができたデータの割合
　・たくさんある陽性データのうち、どれくらい取りこぼしなく網羅することが
　　できたかを示す指標
　・どれくらいしっかり当てられるか、正解を見つけ出せるか、見極めができるか
　・この値が高いほど、誤った判断が少ないことを意味する
　・精度(Precision)と再現率(Recall)はトレードオフの関係となる

Python関数

　Pythonのscikit-learnライブラリでのPrecisionの使用方法

Precision関数

sklearn.metrics.precision_score(x_true, x_pred, labels=None, pos_label=1, average='binary', sample_weight=None, zero_division='warn')
# x_true：正解値のデータ
# x_pred：予測値のデータ
# 3番目以降のパラメータは省略可

　Pythonのscikit-learnライブラリでのRecallの使用方法

Recall関数

sklearn.metrics.recall_score(x_true, x_pred, labels=None, pos_label=1, average='binary', sample_weight=None, zero_division='warn')
# x_true：正解値のデータ
# x_pred：予測値のデータ
# 3番目以降のパラメータは省略可

F1-Score / Fβ-Score

　F1-Scoreは以下のように定義されます。

\begin{align}
F1-Score &= \frac{2}{\frac{1}{Recall}+\frac{1}{Precision}}\\
&=\frac{2・Recall・Precision}{Recall + Precision}\\
&=\frac{2TP}{2TP+FP+FN}
\end{align}

<解説>
　・精度(Precision)と再現率(Recall)の調和平均
　・精度(Precision)、再現率(Recall)それぞれ単独で使用することよりも、調和平均を
　　指標として用いることが一般的
　・F1値と呼ぶ

　Fβ-Scoreは以下のように定義されます。

\begin{align}
F_\beta-Score &= \frac{(1+\beta^2)}{\frac{\beta^2}{Recall}+\frac{1}{Precision}}\\
&=(1+\beta^2)\frac{Precision・Recall}{(\beta^2+Precision)+Recall}
\end{align}

<解説>
　・F1-Scoreをもとに、再現率(Recall)をどのくらい重視するかを表す係数βで調整した
　　評価指標(精度と再現率のバランスを係数βで調整する)

Python関数

　Pythonのscikit-learnライブラリでのF1-Scoreの使用方法

F1-Score関数

sklearn.metrics.f1_score(x_true, x_pred, labels=None, pos_label=1, average='binary', sample_weight=None, zero_division='warn')
# x_true：正解値のデータ
# x_pred：予測値のデータ
# 3番目以降のパラメータは省略可

　Pythonのscikit-learnライブラリでのFβ-Scoreの使用方法

F1-Score関数

sklearn.metrics.fbeta_score(x_true, x_pred, labels=None, pos_label=1, average='binary', sample_weight=None, zero_division='warn')
# x_true：正解値のデータ
# x_pred：予測値のデータ
# 3番目以降のパラメータは省略可

(2-2)確率を予測値とする二値分類の評価関数

ここでは、分類タスクにおいて、Aクラスに入るかBクラスに入るかを求めるケースではなく、Aクラスに入る確率、またはBクラスに入る確率が得られるケースで、その確率の精度を評価する指標を取り扱います。

LogLoss(対数損失)

　評価関数の値(誤差)をE(x)とすると、

\begin{align}
E(x) &= -\frac{1}{n}\sum_{i=1}^{n}\big\{ x_i\log p_i + (1-x_i)\log (1-p_i) \big\}\\
&= -\frac{1}{n}\sum_{i=1}^{n}\log \acute{p_i}\\
\end{align}\\
n：データ数\\
x_i：陽性(Positive)かどうかの真偽値(陽性は1、陰性は0)\\
p_i：i番目のデータが陽性と予測した確率\\
\acute{p_i}：正解を予測している確率

<解説>
　・誤差E(x)の値が低いほど予測精度が高い
　・予測した確率値の度合い(乖離)も結果に反映される
　・陽性(Positive)である確率を低く算出したにも関わらず正解が陽性の場合や、
　　反対に、陽性である確率を高く算出したにもかかわらず正解が陰性(Negative)の
　　場合は大きなペナルティが与えられる

Python関数

　Pythonのscikit-learnライブラリでのLogLossの使用方法

LogLoss関数

sklearn.metrics.log_loss(x_true, x_pred, eps=1e-15, normalize=True, sample_weight=None, labels=None)
# x_true：正解値のデータ
# x_pred：予測値のデータ
# 3番目以降のパラメータは省略可

AUC(対数損失)

　AUCを解説する前に、ROC曲線について確認します。

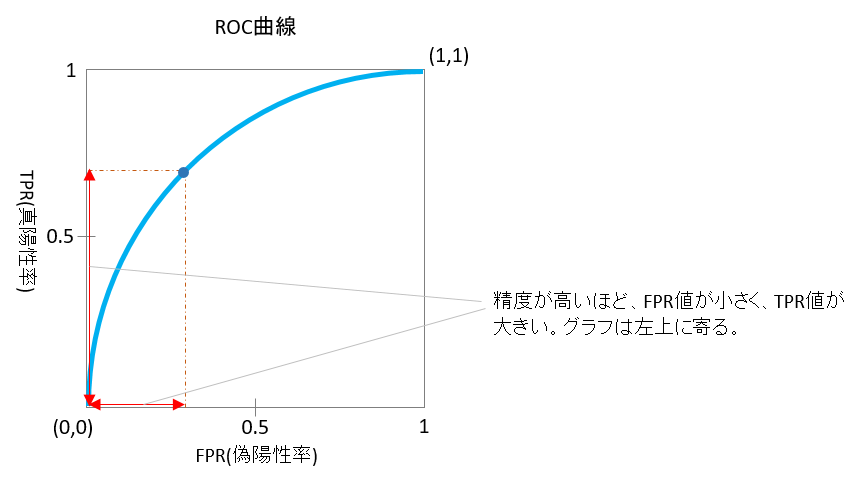
　ROC曲線(Receiver Operating Characteristic)(または推測曲線)とは、
　　縦軸にTPR(真陽性率：True Positive Rate)、横軸にFPR(偽陽性率：
　　False Positive Rate)を描いたものです。

　　特徴は、
　　(1)図3の通り、原点(0,0)と右上の交点(1,1)を結ぶ線
　　(2)精度が高く偽陽性率が低い状態は、グラフは左上に寄る
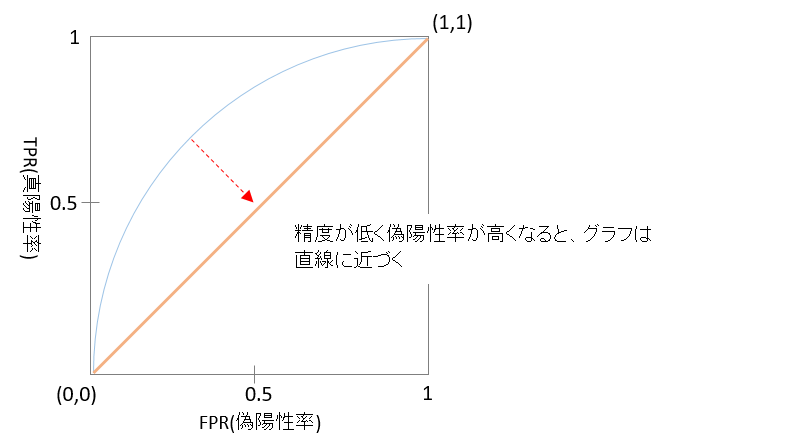
　　(3)精度が低く偽陽性率が高くなると、グラフは直線に近づく

図3

　AUC：Area Under the Curve
　AUCはROC曲線の曲線の下部の領域の面積を意味します。

　
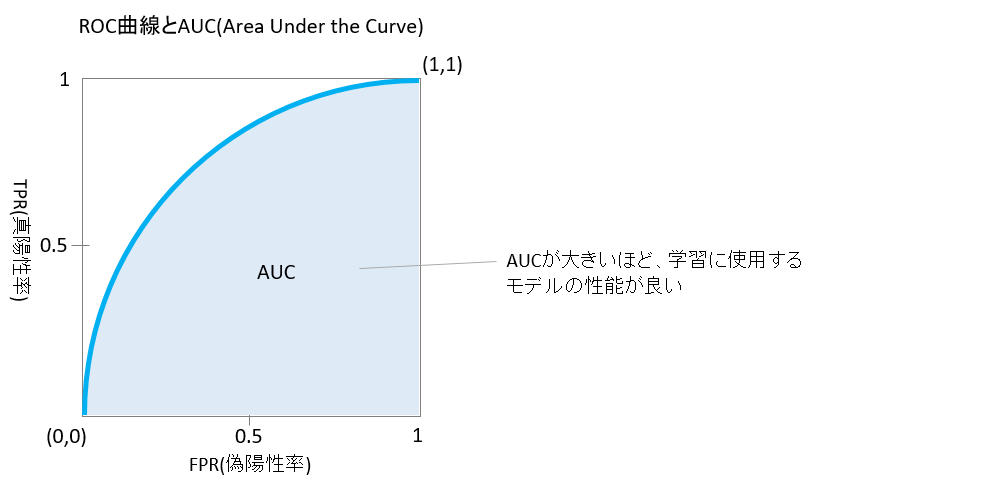
<解説>
　・精度が高いほどROC曲線が左上に寄るため、AUC(面積)も大きくなる
　・AUCが大きいほど、学習に使用するモデルの性能が良い

Python関数

　Pythonのscikit-learnライブラリでのAUCの使用方法

ROC_AUC関数

sklearn.metrics.roc_auc_score(x_true, x_pred, average='macro', sample_weight=None, max_fpr=None, multi_class='raise', labels=None)
# x_true：正解値のデータ
# x_pred：予測値のデータ
# 3番目以降のパラメータは省略可

(3)多クラス分類(マルチクラス分類)の評価関数

多クラス分類(マルチクラス分類)は、分類先のグループ(クラス)が3つ以上ある場合の分類タスクです。評価関数は基本的に二値分類の関数を応用したものとなります。

Multi-Class Accuracy(他クラス正解率)

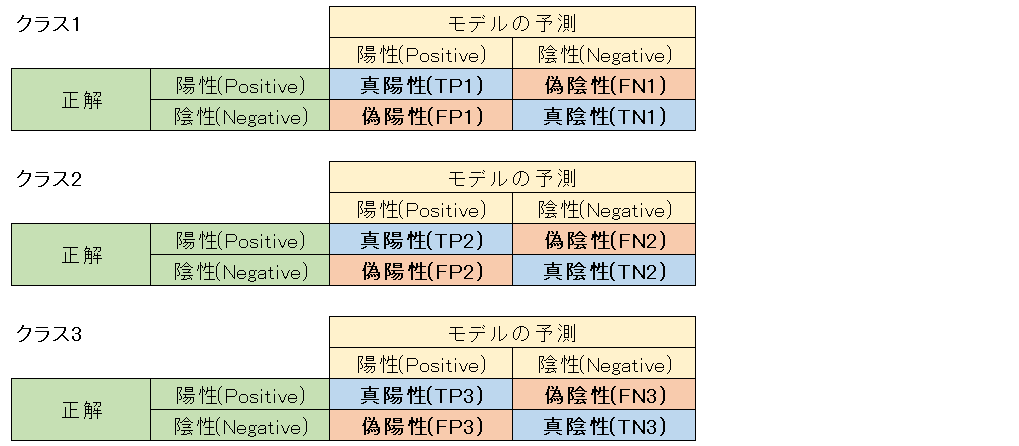
　例として、3つのクラスが存在する場合に、それぞれのクラス1～3の混同行列を考ると図4のようになります。

図4

　Multi-Class Accuracyは以下のように定義されます。

Multi-Class Accuracy = \frac{1}{3}\bigg( \frac{TP_1+TN_1}{TP_1+TN_1+FP_1+FN_1}+\frac{TP_2+TN_2}{TP_2+TN_2+FP_2+FN_2}+\frac{TP_3+TN_3}{TP_3+TN_3+FP_3+FN_3}\bigg)

Python関数

　Pythonのscikit-learnライブラリでのMulti-Class Accuracyの使用方法

Multi-Class_Accuracy関数

sklearn.metrics.accuracy_score(x_true, x_pred, normalize=True, sample_weight=None)
# x_true：正解値のデータ(クラスをまたぐ)
# x_pred：予測値のデータ(クラスをまたぐ)
# 3番目以降のパラメータは省略可

Multi-Class LogLoss(他クラス対数損失)

　Multi-Class LogLoss(他クラス対数損失)は以下のように定義されます。

Multi-Class LogLoss = -\frac{1}{n}\sum_{i=1}^{n}\sum_{j=1}^{m}x_{ij} \log p_{ij}\\
n：データ数\\
m：クラス数\\
x_{ij}：i番目のデータがjクラスに属するかどうかの真偽値(属する場合は1、属さない場合は0)\\
P_{ij}：i番目のデータがjクラスに属する予測確率

Mean-F1、Macro-F1、Micro-F1

　二値分類で使用するF1-Scoreを他クラス分類用に拡張した評価関数です。
　Mean-F1、Macro-F1、Micro-F1の3つを確認します。

評価関数	内容
Mean-F1	データごとにF1-Scoreを求め、その平均を取ったもの
Macro-F1	各クラスごとのF1-Scoreを求め、その平均を取ったもの
Micro-F1	各データの予測値からTP,TN,FP,FNそれぞれをカウントし、これらの混同行列からF1-Scoreを求めたもの

Python関数

　Pythonのscikit-learnライブラリでのMean-F1,Macro-F1,Micro-F1の使用方法。
　Mean-F1の場合はaverage='samples'、Macro-F1の場合はaverage='iacro'、
　Micro-F1の場合はaverage='micro'とします。、

Mean-F1,Macro-F1,Micro-F1関数

sklearn.metrics.f1_score(x_true, x_pred, lables=None, pos_label=1, average='binary', sample_weight=None, zero_division='warn')

出典

■参考書
「Kaggleで学んでハイスコアをたたき出す！Python機械学習＆データ分析」
　チーム・カルポ著／秀和システム

ご意見など

ご意見、間違い訂正などございましたらお寄せ下さい。