コンピュータとオセロ対戦5 ～n手先まで読んで返す～

前回

今回の目標

前回までで、（しようと思えば）n手先まで読んで返すプログラムはできました。
しかし無駄な関数が多いので削っていきたいと思います。
ここで紹介しているプログラムが、前回までで言っていた「完成版」です。

ここから本編

方針

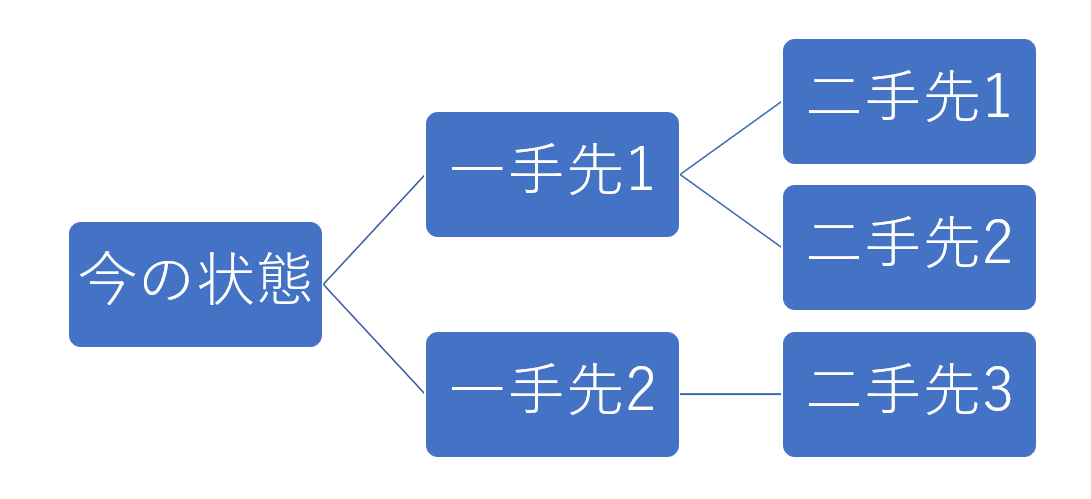
方針としては変わらず、下図のように全ての手を考え、最終的に最も有利になる場所に置くことです。

プログラムでどう実現する？

まず構造体はなくします。
なぜかというと、盤面をいちいち保存しておく必要はなく、重要なのはスコア（自分の駒の数-相手の駒の数）だからです。
次に再起関数を作ります。
一手増えるごとに関数の数まで増やしていると大変だからです。

上図において、最終的な地点ではその場でのスコアを返し、途中の部分では帰ってきたスコアの平均を返します。こうして、最終的に「今の状態」で、平均値が高い所へ駒を置くことで強くなるのではないかと考えました。

mainの上に書くやつ

無駄な関数を減らすには、思考用のcheckと普段用のcheck、思考用のputと普段用のput・・・と分けずに、それぞれ一つの関数で実現させることが必要になります。
それを考えると下のようになりました。
なお、「READ_NUM」は「n手先まで読んで返す」の「n」にあたる部分です。
print関数はなぜかprintbに改名しました。

nhand.c

#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include <stdbool.h>

#define READ_NUM 5
#define SIZE 8
#define NONE 0
#define BLACK 1
#define WHITE 2

bool check(char board[SIZE][SIZE], int line, int col, bool turn);
bool all_none(char board[SIZE][SIZE]);
void count_last(char board[SIZE][SIZE]);
int count(char board[SIZE][SIZE], bool turn);
int check_all(char board[SIZE][SIZE], bool turn);
void setup(char board[SIZE][SIZE]);
void printb(char board[SIZE][SIZE]);
void que(int * line, int * col);
void put(char board[SIZE][SIZE], int line, int col, bool turn);
void think(char board[SIZE][SIZE], int * line, int * col, bool turn);
int board_add(char board[SIZE][SIZE], int line, int col, bool turn, int num);

基本的な関数の使い方

ほぼすべての関数で二次元配列が渡されていますが、この引数が「シミュレーション中の盤面」なのか「メインの、普通に表示されるほうの盤面」なのかで関数の働きが変わります。
checkやputなどは、引数の種類によってやることが変わるという感じです。

think

今までと同様、think関数の中にboard_add関数を入れます。
thinkは今までとあまり変わりません。
置けるところを探してboard_add関数を呼び出し、スコアを受け取り、最終判断までしています。

nhand.c

void think(char board[SIZE][SIZE], int * line, int * col, bool turn){
    int i, j;
    int score = 0, max_score = -SIZE * SIZE, run_num = 0;
    int line_num[SIZE << 1], col_num[SIZE << 1];

    for (i = 0; i < SIZE; i++){
        for (j = 0; j < SIZE; j++){
            if (check(board, i + 1, j + 1, turn)){
                score = board_add(board, i + 1, j + 1, turn, 0);
                if (score > max_score){
                    run_num = 0;
                    max_score = score;
                    line_num[run_num] = i;
                    col_num[run_num] = j;
                }else if (score == max_score){
                    run_num++;
                    line_num[run_num] = i;
                    col_num[run_num] = j;
                }
            }
        }
    }

    if (run_num > 0){
        run_num = rand() % (run_num + 1);
        line_num[0] = line_num[run_num];
        col_num[0] = col_num[run_num];
    }

    *line = line_num[0] + 1;
    *col = col_num[0] + 1;

    return;
}

board_add

再起関数にしたことで、前よりは短くなったと思います。
やっていることとしては、

1. 新しい盤面を作り、今の盤面をコピペする
2. コピペした盤面の指定された位置に駒を置く。
3. もしこの関数が指定回数呼び出されていたら、この時のスコアを返して終了。
4. また置けるところを探し、board_add関数を呼び出す。
5. もしその先に置けるところがなかったら、その段階でのスコアを返す。

という感じです。

nhand.c

int board_add(char board[SIZE][SIZE], int line, int col, bool turn, int num){
    int i, j;
    int score = 0, run_num = 0, score_ele;
    char board_leaf[SIZE][SIZE];
    char * line_array;

    for (i = 0; i < SIZE; i++){
        line_array = board_leaf[i];
        for (j = 0; j < SIZE; j++){
            line_array[j] = board[i][j];
        }
    }
    put(board_leaf, line, col, turn);

    if (num == READ_NUM) return count(board_leaf, false);

    for (i = 0; i < SIZE; i++){
        for (j = 0; j < SIZE; j++){
            if (check(board_leaf, i + 1, j + 1, turn)){
                score_ele = board_add(board_leaf, i + 1, j + 1, !turn, num + 1);
                if (score_ele == -1) score_ele = count(board_leaf, false);
                score += score_ele;
                run_num++;
            }
        }
    }

    if (run_num == 0) return -1;

    return score / run_num;
}

フルバージョン

この中から「nhand.c」を探してください。

実際にやってみる

6手先を超えると計算に時間がかかるようになり、9手先くらいでまともにプレイできなくなりました。
5手先くらいが限界だと思います。
今までよりは強かったですが、人相手に安定して勝てるような実力はありませんでした。
また、「READ_NUMの値を大きくすればするほどつよいのでは？」と思いましたがそうでもなかったです。

次回は

実はここから先の計画はあまりなく、

• 人工知能でやってみる案
• 入力ではなく、クリック操作でプレイできるようにする案

があります。
次回何をするかはまだ確定してません。

(追記)　後者のクリック操作のほうをしました。
次回