※コメントでの助言、大変ありがとうございました。13までは予定がありましたので14以降で反映させていただきます。
今回の目標
前回決めた方針を煮詰め、より実際に使える形にしていきたいです。
ここから本編
データ集め方法の検討
まずは前回決めた方針を少しいじり、より正解率が上がらないか試します。
それぞれの案で前回のプログラムを少し変更したものを使っています。
前回の学習結果 turnnum_and_num_
参考までに前回の学習結果。
LogisticRegression:
train score: 0.38835591599907693
test score: 0.39589262364433503
DecisionTreeClassifier:
train score: 0.41779579995384564
test score: 0.38643181293746637
KNeighborsClassifier:
train score: 0.39761975406323147
test score: 0.36374125067302515
改善案1 turnnum_and_num_all
前回、print関数内のfor分の繰り返し数統一のためボードが埋まることなく終わった試合のデータは使いませんでしたが、よく考えたらそんなことをする必要はない気がしたのですべてのデータを使ってみました。
正解率はほぼ変わらない結果になりました。
LogisticRegression:
train score: 0.38835591599907693
test score: 0.39589262364433503
DecisionTreeClassifier:
train score: 0.41779579995384564
test score: 0.38643181293746637
KNeighborsClassifier:
train score: 0.39761975406323147
test score: 0.36374125067302515
改善案2 tunnnum_and_num_very
今度は、ボードが埋まることなく終わった時のデータ、つまり圧勝したデータのみを集めてみました。
そうそうないことなので前回のようにたまたま埋まらなかったデータを集めるわけにもいかず、下に示すプログラムによって荒業で1000勝分のデータを集めました。
ちなみに今までのデータ集めは1秒弱で終わっていましたが、これは1300秒ほどかかってしまいました(笑)。
void main(void) {
double start = clock();
int turn_num;
bool can, old_can;
FILE * fp;
if (PLAYER == BLACK) fp = fopen("whitedata.txt", "w");
else fp = fopen("blackdata.txt", "w");
if (fp == NULL){
printf("text file error\n");
exit(-1);
}
for (int num = 0; num < NUM; num++){
setup();
srand((unsigned int)time(NULL) + num + rand());
while (!win()){
turn = BLACK;
can = true, old_can = true;
turn_num = 0;
setup();
// printb();
while ((can = check_all()) || old_can){
if (can){
think(turn_num);
// printb();
turn_num++;
}
old_can = can;
turn = 3 - turn;
}
}
if (turn_num == SIZE * SIZE - 4) num--;
else print(fp, turn_num);
}
fclose(fp);
printf("実行時間: %.4lf[s]\n", (clock() - start) / 1000000);
}
学習結果はこちら。
0.5で喜ぶのもどうかと思いますがかなりいいですね。
LogisticRegression:
train score: 0.44214327830188677
test score: 0.45581155433287485
DecisionTreeClassifier:
train score: 0.5016214622641509
test score: 0.47420907840440163
KNeighborsClassifier:
train score: 0.47973172169811323
test score: 0.44411966987620355
改善案3 tunnnum_and_num_time
試合を序盤、中盤、終盤に分け、それぞれで学習を行いました。
1が序盤、2が中盤、3が終盤です。
どれもぱっとしない正解率となりました。
whitedata1.txt :
LogisticRegression:
train score: 0.39283109304991143
test score: 0.39620807000486147
DecisionTreeClassifier:
train score: 0.4116911534854642
test score: 0.3889158969372873
KNeighborsClassifier:
train score: 0.39137230384495153
test score: 0.3765192027224113
whitedata2.txt :
LogisticRegression:
train score: 0.396020646020646
test score: 0.390561274033793
DecisionTreeClassifier:
train score: 0.4165834165834166
test score: 0.38201592542241214
KNeighborsClassifier:
train score: 0.38727938727938727
test score: 0.3688094775684599
whitedata3.txt :
LogisticRegression:
train score: 0.392617795649036
test score: 0.4046187154197739
DecisionTreeClassifier:
train score: 0.4225177853386947
test score: 0.380322347847005
KNeighborsClassifier:
train score: 0.4030312403340551
test score: 0.3625210488332932
改善案4 tunnnum_and_num_state
今有利であるか不利であるかを分け、それぞれ学習させました。
有利である時がwin、不利である時をloseとして別のファイルに分けてデータを保存しました。
whitedatawin.txt :
LogisticRegression:
train score: 0.37343347820583145
test score: 0.3797007284898602
DecisionTreeClassifier:
train score: 0.39326553863032193
test score: 0.37536916715888957
KNeighborsClassifier:
train score: 0.37769526140343473
test score: 0.3690687143138413
whitedatalose.txt :
LogisticRegression:
train score: 0.4491049261727427
test score: 0.4294422432185309
DecisionTreeClassifier:
train score: 0.460734352541487
test score: 0.4126790612618104
KNeighborsClassifier:
train score: 0.4298967725075134
test score: 0.39073453215483084
改善案5 tunnnum_and_num_random
今までお互い同じ考え方で打ち合わせていましたが、今回、コンピュータは「1~3番目に多くひっくりかえせる場所のどこか」に、プレイヤー(役)は「置ける場所からランダムに」置くという手法を試してみました。
今までにないアプローチですが正解率は上がりました。
LogisticRegression:
train score: 0.4285224898085026
test score: 0.42482615298537285
DecisionTreeClassifier:
train score: 0.644650748518379
test score: 0.6312045400047958
KNeighborsClassifier:
train score: 0.627487924360248
test score: 0.6157781152585725
改善案6 tunnnum_and_num_various
上で試した方法は、正解率こそ高いものの現実的ではありません。そのため今回、プレイヤー(役)は今までC言語で作った
- ランダムに返す
- 一手先まで読んで返す
- 二手先まで読んで返す
- n手先まで読んで返す
の中からランダムに手法を選び打ち返すという設定にしました。
なおn手先は5手先までしてもらう予定だったのですが、データづくりが30分経っても終わらなかったため3手先までで妥協しました。
プログラムの試合部分はこのようになりました。
なお、細かい部分は変更しています。
while ((can = check_all()) || old_can){
if (can){
if (turn == PLAYER){
int func = rand() % 4;
if (func == 0){
random_put();
}else{
READ_NUM = func;
nhand();
}
}
else think(turn_num);
// printb();
turn_num++;
}
old_can = can;
turn = 3 - turn;
}
学習結果は以下のようになりました。
LogisticRegression:
train score: 0.40939101728781163
test score: 0.41147258538562886
DecisionTreeClassifier:
train score: 0.5301885153331596
test score: 0.510084118779771
KNeighborsClassifier:
train score: 0.5358352879854053
test score: 0.5206243032329989
改善案7 tunnnum_and_num_middle
改善案3から着想を得て、最初の何手かと最後の何手かは勝敗にあまり影響しないのでは?と考えました。
そこで最初の五手と最後の五手をデータとして取得せずに学習させてみました。
LogisticRegression:
train score: 0.39835757533579236
test score: 0.397580579686612
DecisionTreeClassifier:
train score: 0.41436425638527385
test score: 0.38994885118129413
KNeighborsClassifier:
train score: 0.388301203980792
test score: 0.37484777137289926
改善案8 turnnum_and_num_state_various
正解率の高かった改善案4と6を合体させてみました。
(単純に正解率を見れば案5が最大ですが、現実的ではないと判断したため採用しないことにしました)
すなわち、プレイヤー(役)は
- ランダムに返す
- 一手先まで読んで返す
- 二手先まで読んで返す
- n手先まで読んで返す
のいずれかの手法で打ち返し、コンピュータは、自分が優勢である時と劣勢である時のデータを分けて保存しそれぞれ学習させます。
改善案4と6、どちらにも勝る正解率となりました。
whitedatawin.txt :
LogisticRegression:
train score: 0.3968915516193453
test score: 0.40316045380875204
DecisionTreeClassifier:
train score: 0.5382912216723105
test score: 0.5249189627228525
KNeighborsClassifier:
train score: 0.57028740123296
test score: 0.5558144246353323
whitedatalose.txt :
LogisticRegression:
train score: 0.46552675124103693
test score: 0.46846846846846846
DecisionTreeClassifier:
train score: 0.5146166574738004
test score: 0.4851994851994852
KNeighborsClassifier:
train score: 0.47766133480419193
test score: 0.4453024453024453
学習方法の検討 learnmethod_test
前回の学習方法
前回は、以下のプログラムを使用していました。といっても全てのパラメータをとりあえずで決定し、なおかつ様々な方法を使用していました。
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.tree import DecisionTreeClassifier
from sklearn.neighbors import KNeighborsClassifier
x = []
y = []
with open("whitedata.txt", "r") as data:
for num in data:
x.append([])
for i in range(3):
x[-1].append(int(num[0:3]))
num = num[3:]
y.append(int(num.strip("\n")))
if y[-1] == -1:
del x[-1]
del y[-1]
# print(x)
# print(y)
x_train, x_test, y_train, y_test = train_test_split(x, y,
test_size=0.3,
random_state=0)
model = LogisticRegression()
model.fit(x_train, y_train)
print("LogisticRegression:")
print("train score:\t", model.score(x_train, y_train))
print("test score:\t", model.score(x_test, y_test), "\n")
model = DecisionTreeClassifier(criterion="entropy",
max_depth=10,
random_state=0)
model.fit(x_train, y_train)
print("DecisionTreeClassifier:")
print("train score:\t", model.score(x_train, y_train))
print("test score:\t", model.score(x_test, y_test), "\n")
model = KNeighborsClassifier(n_neighbors=10)
model.fit(x_train, y_train)
print("KNeighborsClassifier:")
print("train score:\t", model.score(x_train, y_train))
print("test score:\t", model.score(x_test, y_test))
ここからは正解率が全体的に高かった決定木に絞って学習を行い、かつパラメータを変更しながら正解率の向上を目指しました。
近傍法も善戦していますが、決定木との正解率対決で負け越しているので今回は検証しません。
使用データは、総合的に見て最も現実的かつ正解率の高かった、改善案8(turnnum_and_num_state_various)のwinデータを用います。調査対象以外のパラメータはデフォルト値のままです。random_stateのみ0で固定しています。
検討前の正解率
なお、パラメータは
- criterion="entropy"
- max_depth=10
- random_state=0
です。他はデフォルトのままです。
train score: 0.5382912216723105
test score: 0.5249189627228525
criterionの検討
デフォルト値はgini。
双方とも検討前を上回り、かつほぼ変わらない正解率となりました。
この検討ではmax_depthはデフォルトですので、10は浅すぎましたかね。
entropy :
train score: 0.5971607189372232
test score: 0.5665518638573744
gini :
train score: 0.5971607189372232
test score: 0.56645056726094
splitterの検討
デフォルト値はbest。
またも検討前を上回り、かつほぼ変わらない正解率となりました。
bestとginiの組み合わせがデフォルトコンビとなるわけですが、キチンと全く同じ結果になっています。entropy-best及びgini-randomの組み合わせのトレーニングデータでの正解率が、best-giniのそれと全く同じになっているのが気になりますが・・・。
この検討でもmax_depthはデフォルトですので、やはり10は浅すぎましたかね。
best :
train score: 0.5971607189372232
test score: 0.56645056726094
random :
train score: 0.5971607189372232
test score: 0.5661466774716369
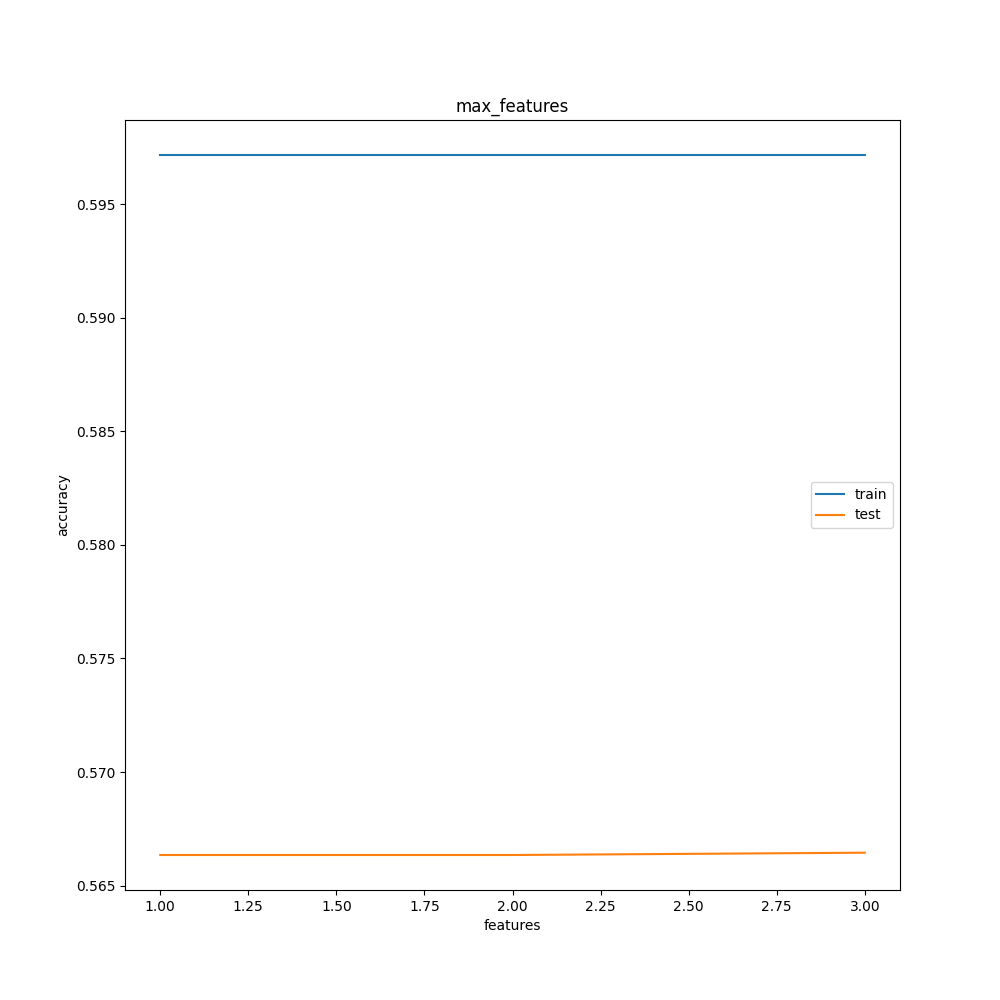
max_featuresの検討
デフォルト値はNone。
面白い結果になりました。
max_featuresはあまりいじる必要はなさそうです。
デフォルト放置でよさそう。
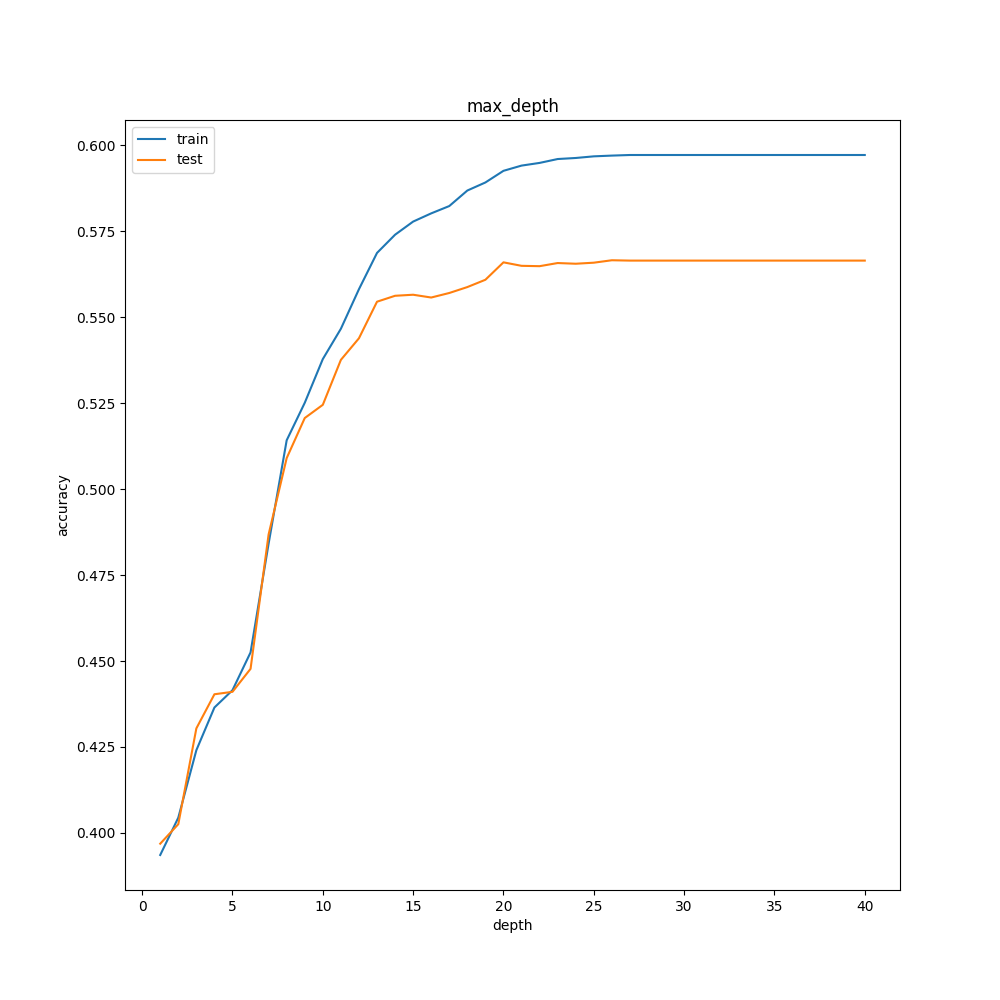
max_depthの検討
デフォルト値はNone。
先ほど「10は浅すぎた」と考察したmax_depthですが、やはりさらに増やすことで正解率は上がるようです。
ただし、深くすればするほどはっきりと過学習が見られたため、それを考慮すると15付近が最適だと考えました。
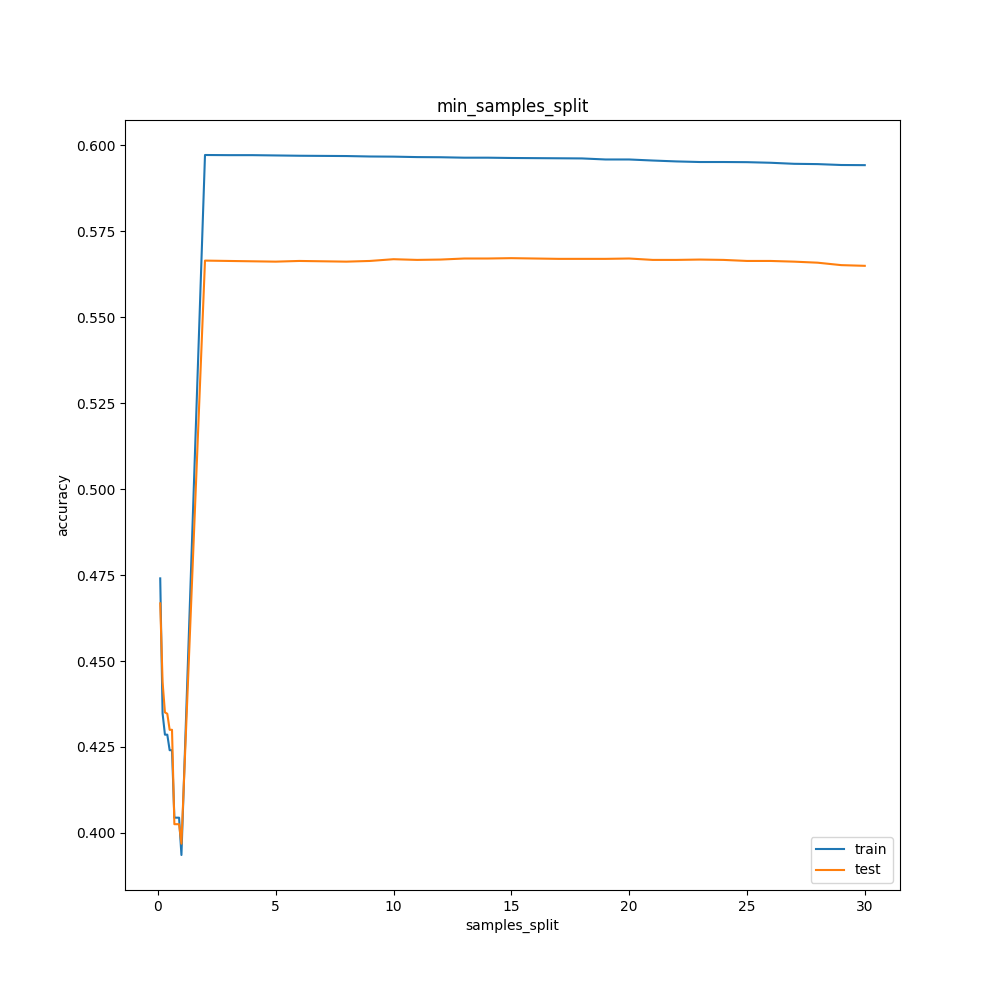
min_samples_splitの検討
ルート記号みたいになりました。
よく分かりませんが、2が最も正解率が高いですね。
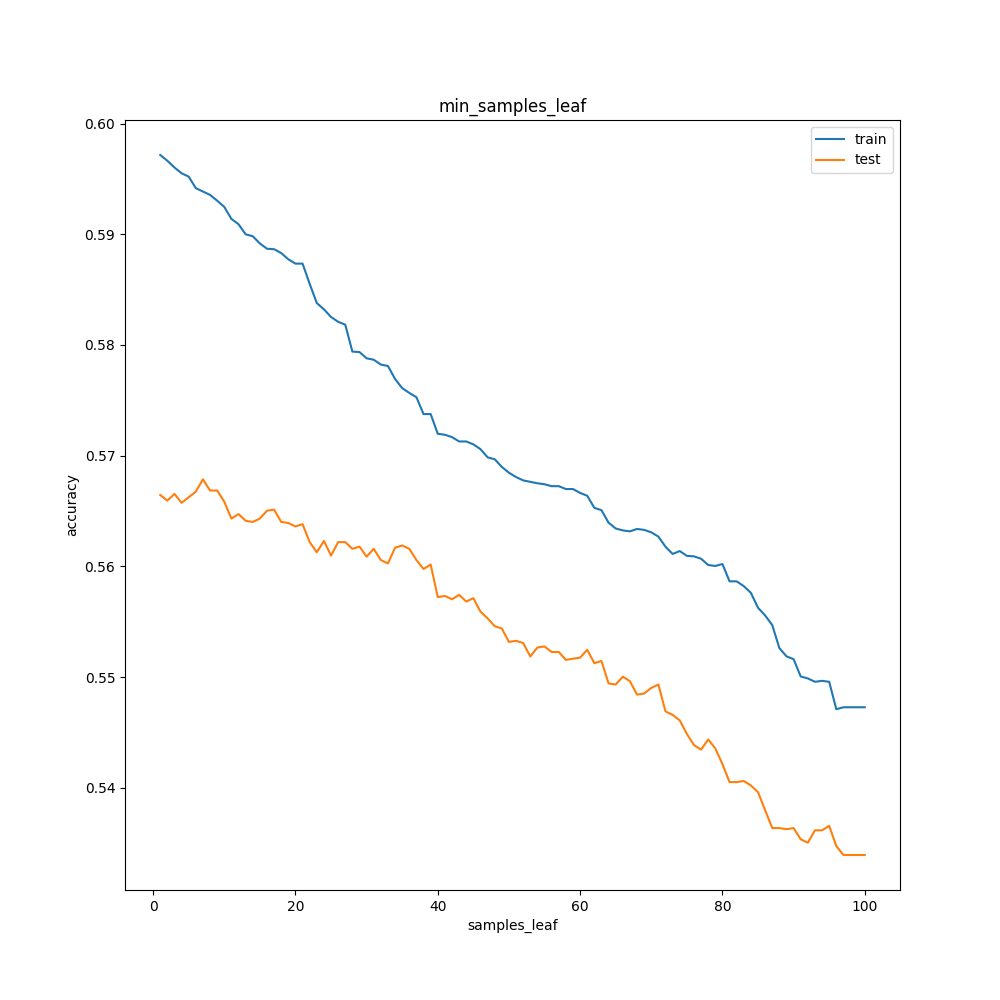
min_samples_leafの検討
トレーニングデータとテストデータの正解率が大きく違うのはmax_featuresと同様ですが、数を上げるほど正解率は下がりました。
ただし40までは、数を上げるほどトレーニングデータとテストデータの正解率の差は小さくなっていっています。
数が小さいほど過学習しやすく、かといって増やせば細やかな分類は難しくなるトレードオフの関係があるようです。
100以降も調べたかったですが、これ以上調べても意味がないかなと考え断念。過学習を恐れるなら35~40程度が最適でしょうか。
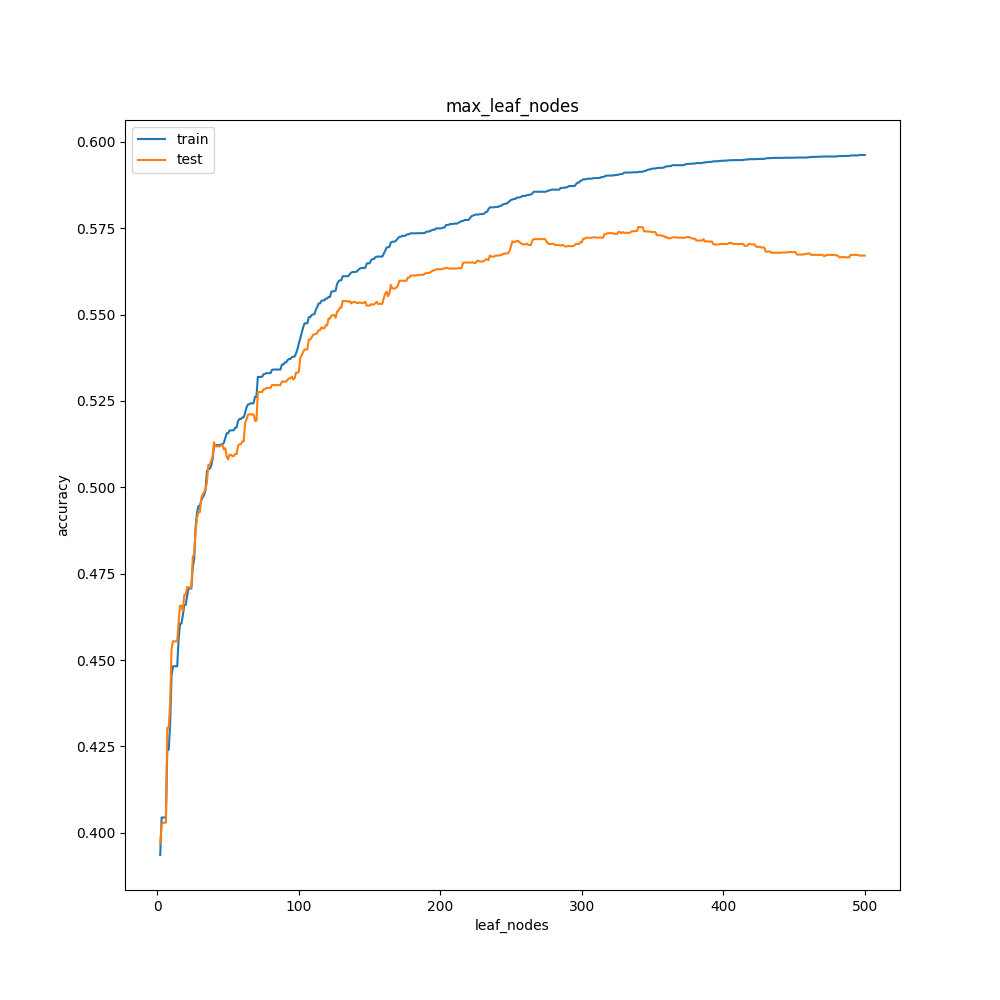
max_leaf_nodesの検証
はい、横軸の数字が半端じゃないですね。
増やしても増やしても特徴があまり変わらなかったので一気に500まで増やしてしまいました。
面白いのは350以降でテストデータの正解率が下がっていることですね。今までは、傾きが変わることはあっても「上がるなら上がる」「下がるなら下がる」という大局的な動きは変わらなかったのですが、途中から下がる結果に。
最適な値を考えるのは難しいですが、自分なら150~200付近を使うと思います。
学習完成版
これまでの検討結果を考慮し、モデルを作り直しました。
model = DecisionTreeClassifier(criterion="entropy",
splitter="best",
max_depth=15,
min_samples_split=2,
min_samples_leaf=35,
random_state=0,
max_leaf_nodes=150)
model.fit(x_train, y_train)
print("train score:\t", model.score(x_train, y_train))
print("test score:\t", model.score(x_test, y_test))
結果は以下の通り。
train score: 0.5608231310237041
test score: 0.5544975688816856
予想よりはるかに低い正解率となりました。
0.6は越えてくると思っていましたがそんなことはなかったです。
フルバージョン
方針の横などに書いている文字列が、この中の12フォルダ内のディレクトリ名に対応しています。
実際にやってみた
まだできません。
次回は
シリーズの11と12を通して、当てずっぽうのように様々な手法を試しましたがどうもずれているようです。
効率よく完成へ向かうため、次回は11と12の考察とまとめを行いたいと思います。