いつになったら「大石泉すき」は揃うのか？

はじめに

この記事は「アイドルマスター Advent Calendar 2020」への参加記事です．この記事ではプログラミングの初心者向けに，Pythonを使用した簡単な統計を解説します．私は業務として開発経験のないにわかプログラマで，この記事も自身の勉強と復習を兼ねているため，間違った記述がある可能性があります．その際はどうぞご指摘ください．

大石泉すきとは

ソーシャルゲーム「アイドルマスターシンデレラガールズ」および，同ゲームの派生リズムゲーム「スターライトステージ」に登場する，プログラミングが趣味のアイドル「大石泉」が好きであるということを表明するネットミームです．初出は定かではありませんが，大石泉を推すプレイヤーの間で使用されており，大石泉のファンでなくても，「大石泉すき」というワードは知っているというプレイヤーも多数いるようです．ちなみに，「すき」は漢字ではなくひらがなが正式なものとされています．
また，「大石泉すき」というコメントに「大石泉すき兄貴すき」とコメントを返すのも，お決まりとなっています．

さらに，その「大石泉すき」というワードを元にしたゲーム（？）が，ウェブサービス「診断メーカー」でもつくられています．「診断メーカー」は入力した自身の名前に応じて，診断を作成したユーザーが設定した値をランダムに返すというジョーク診断サイトです．結果はユーザー名に依存しますが，同じユーザー名でも日替わりで結果を変えるオプションがあります．この「大石泉すき」診断も日替わり変更するものです．

• 大石泉すき | 診断メーカー

私もいち大石泉担当として，ほぼ毎日この診断をしていますが，いつまで経っても完成する気配が見えません．他の方が揃えたという報告も，この診断をやりはじめた2年ほど前から1回だけしか耳にしたことがありません．そこで，今回はこの大石泉すき診断を何回（＝何日）試行すると，「大石泉すき」の完成までこぎつけることができるのか，簡単に調べてみたいと思います．

実際に計算してみる

Pythonで実際に大石泉すき診断を作成し，色々プロットしてみましょう．

大石泉すき診断を実装

手始めに，大石泉すき診断をPythonで実装してみます．
大石泉すき診断は，「大石泉すき」という5文字のうちランダムに1文字を返すというアクションを5回繰り返すものです．乱数の生成が必要になるので，randomライブラリをインポートして表現しましょう．

import random

def randomstring(string):
    n = len(string)
    return ''.join([string[random.randint(0, n-1)] for _ in range(n)])

リスト内包表記を使用しないやり方は以下です．

import random

def randomstring(string):
    n = len(string)
    ans = ''
    
    for _ in range(n):
        m = random.randint(0, n-1)
        ans += string[m]
    
    return ans

これで，引数として与えられた文字列から同数の文字をランダムで選び，文字列として返す関数ができました．
試しに実行すると，

a = randomstring('大石泉すき')
print(a)
# きすす泉き

たしかに，大石泉すき診断と同様に結果を返してくれます（結果はランダムに変わります）．

次に，大石泉すき診断を繰り返し試行して，「大石泉すき」が揃った回数を数える関数をつくります．先程作った関数を利用し，引数として与えられた文字列が何回で揃ったかをint型で返す関数は，以下のように表現できます．

def count_n(string):
    i = 0
    while string != randomstring(string):
        i += 1
    return i

これを実行すると，

a = count_n('大石泉すき')
print(a)
# 2199

これで，大石泉すき診断と，「大石泉すき」が完成するまでにかかった試行回数をカウントする関数が完成しました．

ヒストグラムをプロットする

Pythonで頻出のライブラリmatplotlibを用いて，ヒストグラムを作成してみましょう．

# matplotlibのpyplotをインポートし，pltという名前で使用
import matplotlib.pyplot as plt

# 大石泉すき診断を揃うまで試行し，かかった回数をリストにする．これを1000回繰り返す．
x = [count_n('大石泉すき') for _ in range(1000)]

# xを50階級でヒストグラムにする．
plt.hist(x, bins=20)

# x軸，y軸のラベルとグラフタイトルを設定
plt.xlabel('number of trial')
plt.ylabel('frequency')
plt.title('Ohishi Izumi Suki')

# グラフの表示範囲を自動調整
plt.autoscale(tight=True)

plt.show()

xは以下のようにも書けます．

x = []
for _ in range(1000):
    x.append(count_n('大石泉すき') )

これを実行すると，以下のような画像が出力されます．

余談ですが，plt.hist(x, bins=50, log=True)とすると，グラフを対数グラフにできます．

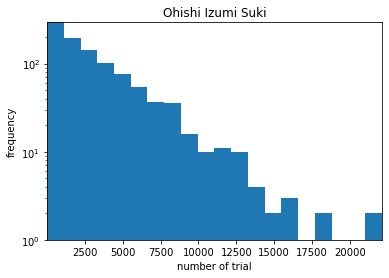
いい感じに直線になってますね．

このグラフを見ると，左端の階級が一番高いですし，割とすぐ「大石泉すき」が揃いそうな感じがします．リストの平均は，statisticsライブラリを用いると，簡単に計算できます．

import statistics

# statisticsライブラリから算術平均を求めるmean関数を使用
x_mean = statistics.mean(x)
print(x_mean)
# 3258.179

今回は，3258回が平均となりました．
平均をグラフに加えてみます．

import matplotlib.pyplot as plt

plt.hist(zzz, bins=20)

# x=3258.179 のグラフを作成
plt.plot([3258.179, 3258.179], [0, 300])

plt.xlabel('number of trial')
plt.ylabel('frequency')
plt.title('Ohishi Izumi Suki')
plt.autoscale(tight=True)

plt.show()

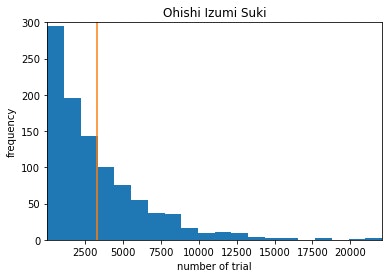
たしかに，平均の線を中心にグラフの面積が半分になっているような感じがします．

確率を計算してみる

ここで，一旦（おそらく就活でSPIを受けて以来に）中学の数学に立ち返ってみます．
大石泉すき診断は，「大石泉すき」という5文字からランダムに5回1文字をピックアップするものです．ハコの中にある文字数は，1回文字をピックアップするごとに少なくなるわけではありません．つまり，大石泉すき診断の結果は

5^5=3125

3125通りになります．
また，大石泉すき診断を1回試行して揃う確率は

\frac{1}{5^5}=\frac{1}{3125}=0.00032

となります．

ここで，n回までに「大石泉すき」が完成する確率は，n回試行したときに「大石泉すき」が1回も揃わない確率から1を引けばいいので，

1-(1-0.00032)^n

です．これをPythonとmatplotlibというライブラリを用いてプロットしてみましょう．

import matplotlib.pyplot as plt

# 試行回数を20000回とする
n = 20000

# x軸:1〜10000までの整数のリストを生成
x = [i for i in range(1, n+1)]

# y軸：i回までに「大石泉すき」が完成する確率のリストを生成
y = [1-(1-0.00032)**i for i in range(1, n+1)]

plt.plot(x, y)
plt.xlim(0, n)
plt.ylim(0, 1)

plt.xlabel('total number of trial')
plt.ylabel('probability')
plt.title('Ohishi Izumi Suki')

plt.show()

xとyは以下のようにしても構いません．

x = []
for i in range(1, n+1):
    x.append(i)

y = []
for i in range(1, n+1):
    n = 1 - (1 - 0.00032) ** i
    y.append(n)

結果，このような画像が出力され，グラフのプロットができました．

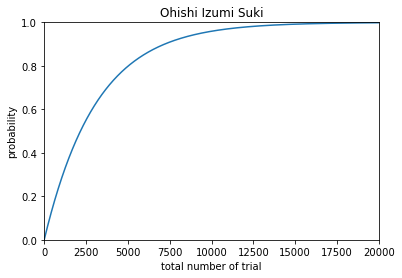
y[19999]
# 0.9983401436533244

また，20000回試行すると，99.8%以上の確率で「大石泉すき」が揃うのがわかります．これを年月日に換算すると，54年10か月と20日です．先に診断メーカーのサービスが終了してそうですね．

for i, e in enumerate(z2):
    if e >= 0.5:
        print(i)
        break
# 2166

また，確率50%を超えるのは2166回目です．こちらも年月日換算で5年11か月と11日かかります．

大石泉すき診断がいつ頃作成されたのか，私が調べた範囲ではわかりませんでした．しかし，Twitterで検索してみたところ，2017年6月末頃から診断の結果が投稿されています．仮に2017年6月頭に作成されたとすると，現在までだいたい1300日程度です．仮に，1日10人が診断をしているならば，試行回数は13000回なので，たしかにひとりは「大石泉すき」を完成させているという体感と近い結果となりました．

先に申し上げましたが，私は大石泉すき診断をはじめてまだ2年程度しか経っておりません．どうやら，私が「大石泉すき」の完成を見るのは当分先のことになりそうです．

おわりに

いかがでしたでしょうか．今回は，ごくごく初歩的な手法で大石泉すき診断の結果を可視化してみました．専門的な統計手法を用いると更に分析をすることができますが，統計学はド素人なので今回の記事の趣旨から若干離れてしまうので，割愛いたします．

これを期に，プログラミングに興味を持った大石泉すき兄貴がいらっしゃいましたら，どの言語でも構いませんので，ぜひ挑戦してみてください．私も参加いたしました，プログラミング初心者のためのアドベントカレンダー「「大石泉すき」 Advent Calendar 2019」等も参考にどうぞ．

最後に，ここまで読んでいただいたこと，御礼申し上げます．そして，Twitter等で大石泉の画像をお見かけした際には，心のなかで「大石泉すき」と唱えてください．そうすれば，あなたも立派な大石泉すき兄貴です．

また，来年またボイスアイドルオーディションが開催されたあかつきには，ぜひ大石泉に票を投じていただけたらと思います．