概要
勉強の一環で、DQNアルゴリズムでぷよぷよの盤面を学習できるかを試してみました。
最新技術ではなく勉強のまとめなのでご容赦ください。
DQN自体をあんまりちゃんと理解してない節があるので、適当なことを書いてたらどうかご連絡ください。
ソースはちょっと長いのでgitへ
https://github.com/KakushiTsuro/puyopuyo_net
やってること
・python(numpy)でのぷよぷよ実装(他の人の実装にもっと簡単なものがある気がする)
・DQNでの学習
DQNとは
そこそこ前に話題になった、強化学習のアルゴリズムです。
Q-learningの盤面評価に深層学習(Deep-learning)を用いたのでDQN(Deep-Q-Network)。
端的に言えば、現在の盤面から以降の盤面で得られるスコアの最大値を予測して、現在取るべき最良の行動を学習します。
詳しい仕組みとかは自分の参考先を御覧ください(丸投げ)。
http://neuro-educator.com/rl1/
実験
学習の目的
今回の記事ではとりあえず、50手番生き残るような学習をさせてみます。
ぷよぷよで50手番生き残ることは決して難しいことではありませんが、完全ランダムでぷよを置くと結構な頻度でゲームオーバーになります。
特に今回のプログラムでは14段目にぷよが置かれるとゲームオーバーという形を取っているのでより死にやすいです。
入力の形
ぷよぷよの盤面は縦13マス×横6マスであり、またぷよの色数は一般的に4色です。つまり、ぷよがない状態を含めて5次元で色を表現できます。なので、入力の形は(13×6×5)としました。
具体的には、
空(1,0,0,0,0)・赤(0,1,0,0,0)…紫(0,0,0,0,1)のような形です。
13×6のサイズの5チャンネル画像だと思えばいいです。
出力の形と行動の種類
出力の数は22です。ニューラルネットワークは22個の出力を返し、その値はその盤面で将来得られるであろうスコアを示します。
このスコアが最も高い番号の出力を、次の行動に対応させます。
出力が22個あるのは、行動の種類が22種のためです。
(6列,端を除いてぷよを横置き×2,縦置き×2 = 44+32 = 22)
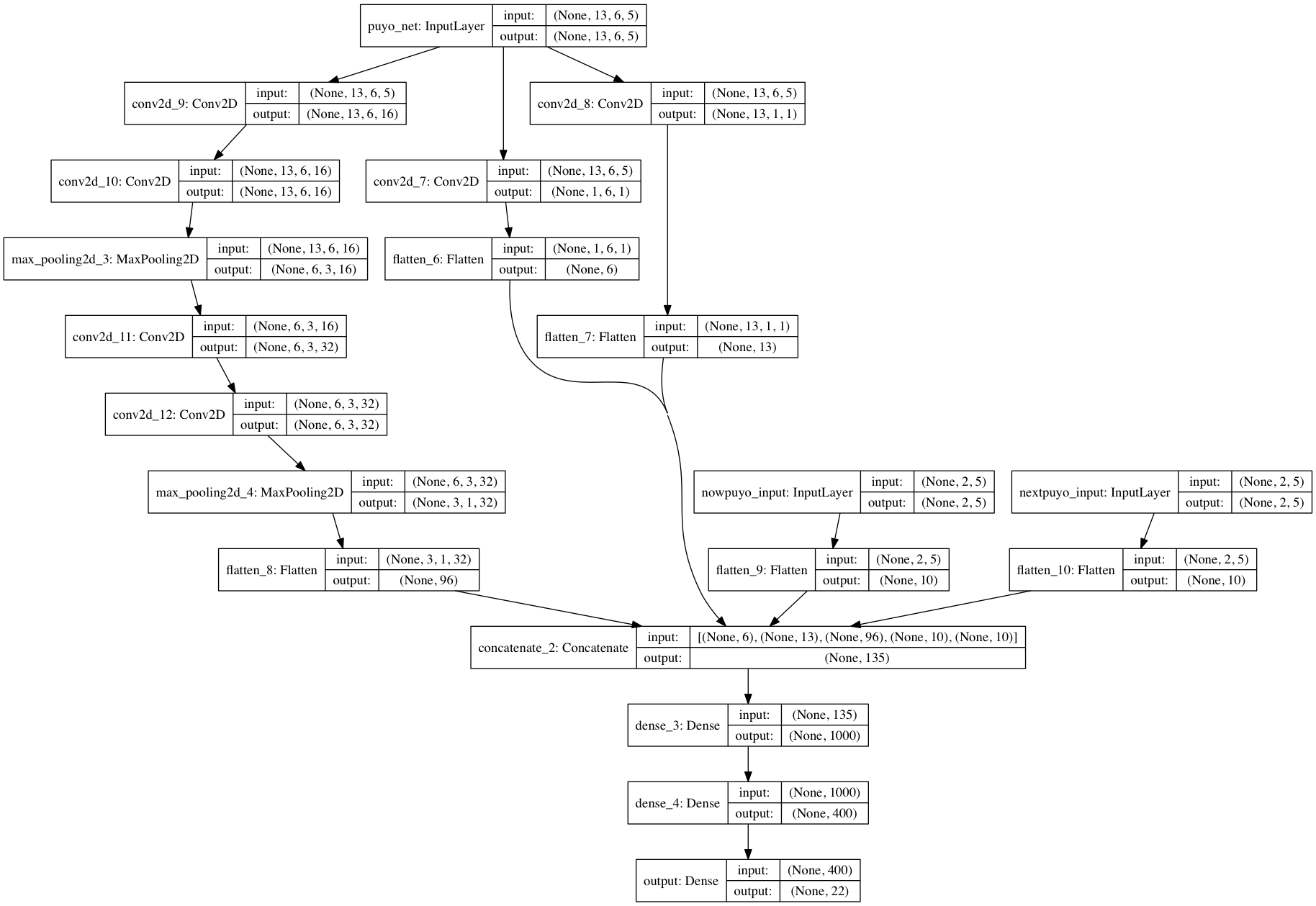
Q関数の構成
一応の目論見としては、入力されたぷよの盤面に対して、縦軸に対して畳み込みを行う層と,横軸に対して畳み込みを行う層、あとは適当に2x2で畳み込みを行う層を組み合わせます。
また、現在降らせるぷよと次に降るぷよのデータも足し合わせ、合計で135次元のデータを作ります。
あとはそれらを全結合層の入力値として計算する形です。
活性化関数は出力層を除いて全てReLUで、出力層のみ線形結合を用いています。
この形で学習がうまくいくかどうかの論理的な部分は皆無です。つまり適当です。
ただ、高さを取る(ように学習してくれそうな)畳込みを行っているのは、ニューラルネットワークの遺伝的アルゴリズムによる学習を用いたテトリスの論文を参考にしています。
報酬
Q学習では、エージェントの行動に対して適宜報酬を与えてやる必要があります。
今回はとりあえず、50手番生き残る事を目的としたいと思います。
なので、50手番でゲームオーバーでなかったら報酬1、ゲームオーバーで報酬-1、それ以外は報酬0を与えることにします(本来はぷよが左から3列目の13段目にぷよが置かれるとゲームオーバーなのですが、めんどくさいので簡略化しました)。
また、ぷよを4つ並べてぷよを消すことを連鎖といいますが、連鎖が発生した場合にも報酬を1与えています。これは起こった連鎖の大きさに合わせて、2連鎖が起こった場合は2、3連鎖が起こった場合には3を与えるようにしています。つまり、大きい連鎖が起こるように学習しています。
報酬の設定は本来1か0に限定されたほうが他の問題へ応用できるのですが、大きい連鎖を優先するように学習させたかったのでこのようにしました。
パラメータ
今回の実験では決めるパラメータは2つで、
・Q-Networkの学習率 : 0.00001
・割引率γ : 0.8
です。
特に重要だったのが割引率γで、これを調整するまで全然学習しませんでした。それについての考察は後半で述べます。
実行環境
python3.5
keras (backendはtheano → channels-last)
3000回学習させています。
GPUは使っていません。
結果
とりあえず、完全ランダムにぷよを置いた場合の結果を示しておきます。
色が見にくいのと、いま落下するぷよとかネクストが見えないのは使用です(表示を忘れてました)。

気持ち結構消せてる気がしないでも無いですが、やっぱり高く積んでしまって死にます。37手番目で死んだようです。
50手番生き残るように学習をさせて見た結果は以下のようになりました。

なんとか50手番生き残りました。
基本的には平たく積むことを意識しています。これは、今回の環境では14段目においたら即ゲームオーバーという性質も大きく関係していると思います。また、なんとなくですが隣接するぷよの色が割と近くなるようにおいている…んじゃないでしょうか。
しかし、とりあえず平たく積んでいること以外には特に連鎖型を意識してるような感じは受けられませんでした。
現状のモデルは、10回中3,4回は50手番生き延びるくらいにはなりましたが、まだまだ35~49手番の間に死んでしまうこともあるので、まだまだ学習が足りないのか、そもそもモデルの形が盤面の情報を学習するのには不向きな形をしているのかを考えてよりよい形に変更する必要がありそうです。ただ、連鎖にもスコアを与えているので、死ぬまで、または50手番生き残る間に得たスコアでも比較してみます。
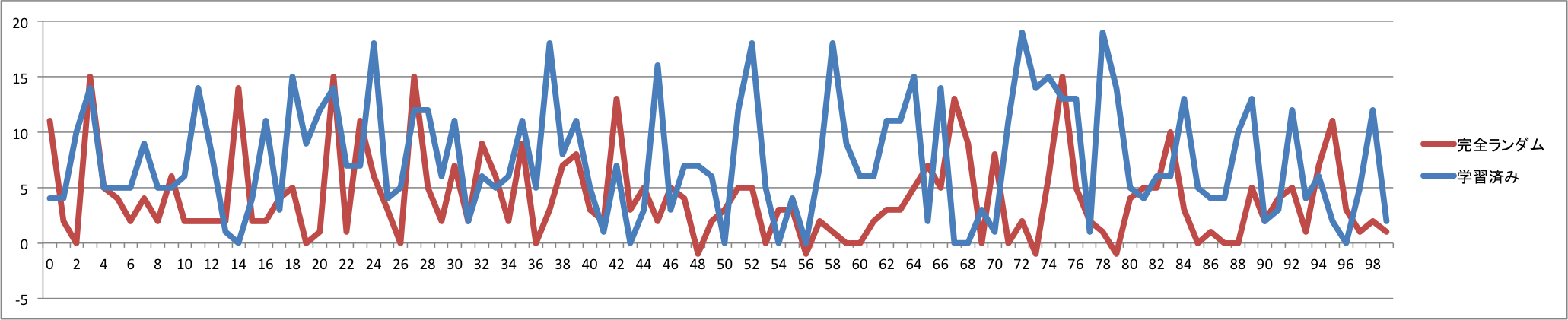
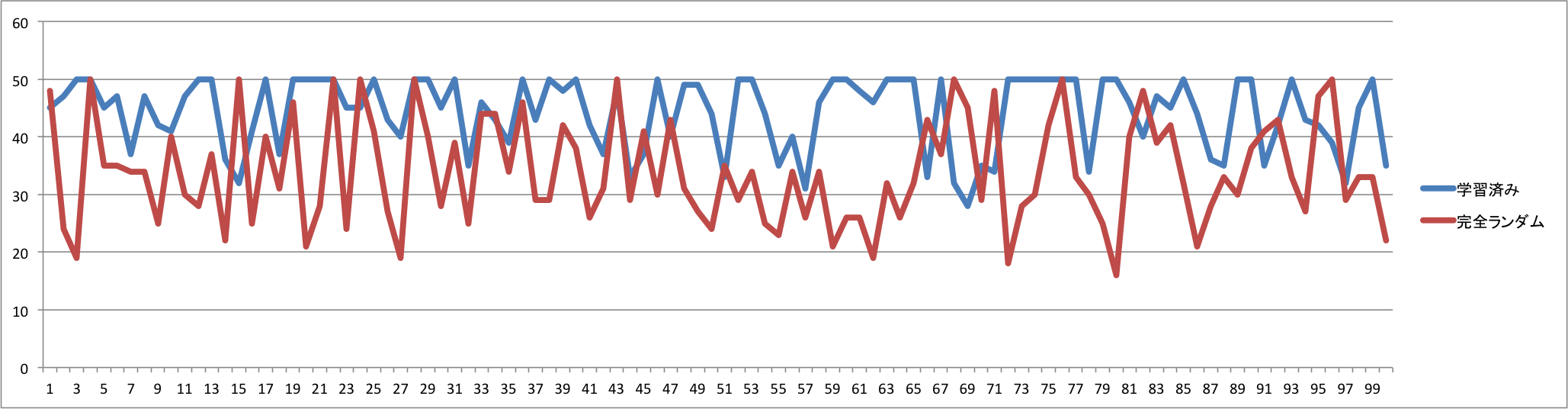
平均値は次のようになりました。
| スコア | ターン数 | |
|---|---|---|
| 未学習 | 4.11 | 33.88 |
| 学習済み | 7.51 | 44.2 |
一応スコアも生存ターン数も伸びているので、学習しているといって良さそうな気がします。
ただ、どのように学習しているのかはやっぱりわからないので正直断定しづらいです。
考察
割引率γについて
当初、割引率γを0.99に設定して学習させていたのですが、全く学習がされませんでした。
その後、割引率を0.8に設定したところ、学習が一気に進展しました。これは、ぷよぷよが完全情報ゲームではなく、不完全情報ゲームであることが大きく関係している気がします。
例えば、割引率を0.99にした状態で15手目でゲームオーバーになってしまった場合、1手目に与えられる割引率は(0.99)^14=0.87になります。しかし、1手目にどこにぷよを置くかが15手目のゲームオーバーの理由にはなるとは考えにくいです。つまり何が言いたいかというと、ぷよぷよ自体は未来の手に関してはランダムであることから、現在直面している盤面における最も良さそうな振る舞いを行うことが求められるのであり、過去に行った手番が及ぼす影響はそんなに大きくないのではないかと思います(実際自分がぷよぷよをしてるときも、やってきたぷよをみて組み方を変えることがほとんどですし)。
今後
とりあえずネットワークで学習は一応できるということはわかったので、次はより長く生き残るか、または3連鎖できるような形を学習するようにしたいです。
考えとしては、3連鎖以上でのみ報酬を与えることで実現できるのではないか、と考えたのですが、そもそも偶然3連鎖ができることが少ない気がします。なので、まずはじめに2連鎖以上でのみ報酬を与えるように学習し、そのモデルを用いて3連鎖以上でのみ報酬がもらえる環境で学習させればいいのかな…とか考えてます。
問題に対してγとかのパラメータも適切な値にしなければならない…のでどうしたものか。