Unityを始めたときからStandardシェーダーが何をしてるか疑問でした
物理ベースシェーディングに入る前にライティングの基礎を学ぶのが目的です
サンプルコードはこちら
https://github.com/tsune2ne/LambertPhongSample
導入
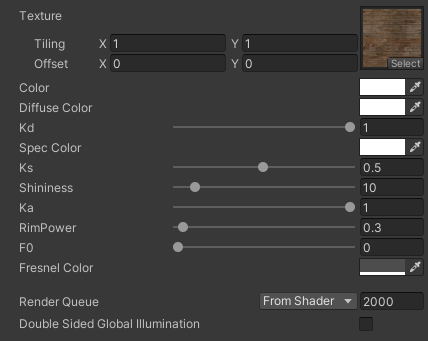
ちなみにUnlitシェーダーに同じ木材テクスチャを当てると下になります

上段にUnlitシェーダー、下段にUnity Standardシェーダーで並べてみます

このUnlitシェーダーをStandardシェーダーに近づけていきましょう
実装項目
・拡散(ディフューズ)反射
・鏡面(スペキュラー)反射
・環境光反射
・フレネル効果
拡散(ディフューズ)反射
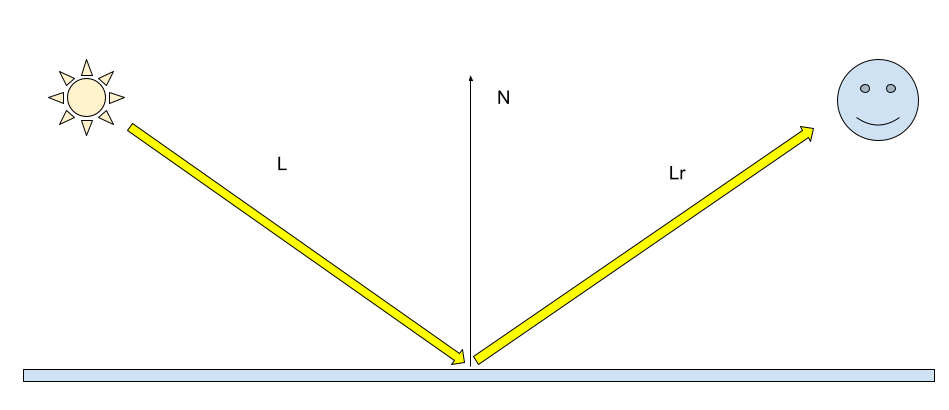
現実世界では物体に光が当たると様々な方向に反射します
光線の反射角が視線に近いほど明るく、遠いほど暗くなります
これは物体のある点について、どの視線でも同じ色になることを示してます
再現するためにランバート反射モデルを実装してみましょう
ランバート反射モデル
理論
ランバート反射を簡単にUnityで実装してみます
L_r=ρ_d(L⋅N)i_d
| 記号 | 意味 |
|---|---|
| $L_r$ | 光の入射が起きた点から、ある方向(大体は観測者の方向)へ放射(反射)する光の量 |
| $ρ_d$ | Lambert反射における反射率。物体の色。アルベド。 |
| $max(0, (L⋅N))$ | コサイン項といいます。法線と入射光のベクトル同士が離れた方向になるほど、この値が小さくなることは知っている方も多いと思います。$L$は光源ベクトル、$N$は表面の法線ベクトル。 |
| $i_d$ | 入射光の強さ |
公式に慣れてないと面を食らいますが、内容はいたってシンプルです
・目に映る物体の色は物体自身の色を反映してる
・反射角に近づくほど明るく、遠のくほど暗くなる
・光が強いほど入射光の色の影響を受ける
これだけです
実装
これをUnityのShaderLabに落とし込みます
ですが$L⋅N$はもう少し補足が必要で、0未満にはなりません
これを式に落とし込みましょう
L_r=ρ_d×max(0,L⋅N)×i_d
↓↓↓ Unityシェーダー化 ↓↓↓
float3 frag(v2f i) : SV_Target
{
float4 col = tex2D(_MainTex, i.uv) * _Color;
float3 lightDir = normalize(_WorldSpaceLightPos0.xyz);
float3 NdotL = dot(i.normal, lightDir);
float3 diffuse = col.xyz * max(0.0, NdotL) * _LightColor0.rgb;
return diffuse;
}
綺麗な影が付いてマットな球になりました
鏡面(スペキュラー)反射
鏡や金属などは光を強く反射します
反射角に露骨に光が跳ね返るため光沢が出ます
これを実装するためにフォン反射モデルを実装します
フォン反射モデル
理論
フォン反射では拡散反射だけでなく鏡面反射、環境光も含めた計算式になっています
L_r=ρ_d(L⋅N)i_d+ρ_s(R⋅V)^αi_s+k_ai_a
| 各項 | 意味 |
|---|---|
| $L_r$ | 光の入射が起きた点から、ある方向(大体は観測者の方向)へ放射(反射)する光の量 |
| $ρ_d(L⋅N)i_d$ | 拡散反射項。ランバート反射モデルそのままです |
| $ρ_s(R⋅V)^αi_s$ | 鏡面反射項。$p_s$は鏡面反射率、$R$は反射ベクトル、$V$は視線ベクトル、$α$は定数で大きいほど鏡に近づきます、$i_s$は入射光の強さ |
| $k_ai_a$ | 環境光項。$k_a$は環境光反射係数、$i_a$は入射光 |
実装
Unityシェーダーに落とし込んでいきましょう
今回は公式を変換して高速化します
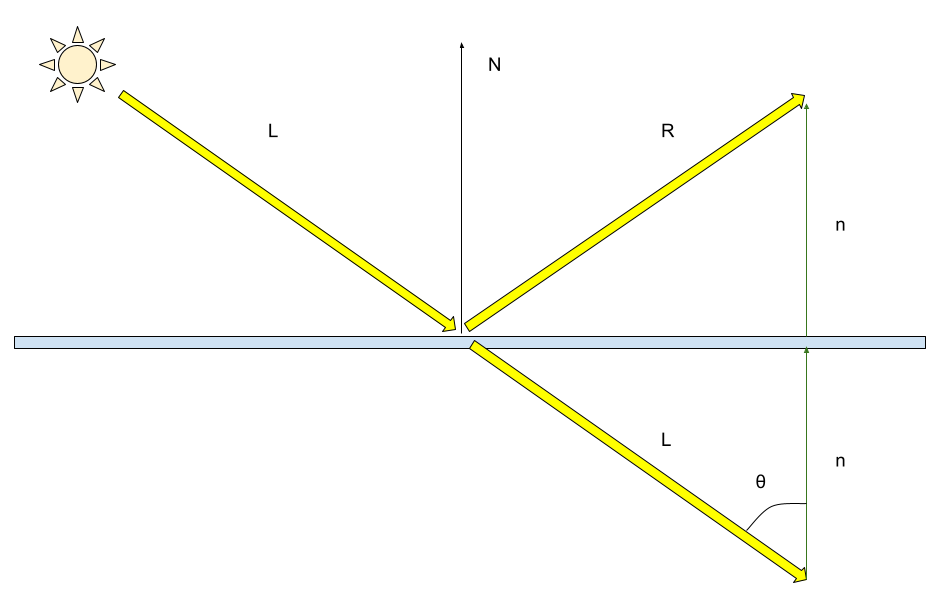
$R$は反射ベクトルなので光源ベクトルと法線ベクトルから計算できます
反射ベクトルRは反射点から入射ベクトルLを伸ばして2回nベクトルを加算すれば算出できます
nベクトルは法線ベクトルNと並行かつNが単位ベクトルなので
n = N * |n|
また三角関数を用いてnベクトルの大きさも表せます
|n| = |L|cosθ
また角度θは法線ベクトルNと入射ベクトルLの内角なので余弦定理第二項で
N・L = |N||L|cosθ
これらを用いてnを計算する
n = N|n| <= nとNは並行かつNは単位ベクトルなので n = N|n|
= N(|L| * cosθ) <= 三角関数より |n| = |L|cosθ
= N(cosθ) <= Lは単位ベクトルなので |L| = 1
= N(L・N) <= N,Lは単位ベクトルなので|N| = |L| = 1
R = L + 2 × n , n = N × (L⋅N)
R = -L + 2N(L⋅N)
L_r=ρ_d(L⋅N)i_d+ρ_s((-L + 2N(L⋅N))⋅V)^αi_s+k_ai_a
例のごとく$L⋅N$と$R⋅V$は0以上の値となります
L_r=ρ_d × max(0, L⋅N) × i_d+ρ_s × max(0, R⋅V)^α×i_s+k_a×i_a
↓↓↓ Unityシェーダー化 ↓↓↓
float4 col = tex2D(_MainTex, i.uv) * _Color;
float3 lightDir = normalize(_WorldSpaceLightPos0.xyz);
float3 NdotL = max(0, dot(i.normal, lightDir));
float3 reflect = normalize(- lightDir + 2.0 * i.normal * NdotL); // 反射ベクトル
float3 diffuse = _Kd * col.xyz * NdotL * _Diffuse; // 拡散反射
float3 spec = _Ks * pow(max(0, dot(reflect, i.view)), _Shininess) * _Specular; // 鏡面反射
float ambient = col.xyz * _Ka * _Ambient; // 環境光
half4 c;
c.rgb = diffuse + spec + ambient;
return c;
鏡面反射がついて滑らかな球になりました
フレネル効果
Standardシェーダーとフォン反射シェーダーを比べると
輪郭がすこし白くなってることに気づくでしょう
光が物体と平行になるほど、反射率が上がります
海の彼方にいくほど、鏡のように空の色を反射していることに気づくでしょう
同じことがStandardシェーダーでも実装されています
今回は簡易的に実装していきます
Schlickの近似式
F_r = F_0 + (1 - F_0)(1 - cosθ)^5
| 各項 | 意味 |
|---|---|
| $F_0$ | 垂直入射の時のFresnel反射係数の実部 |
この近似式の解説は見つからなかったのでスキップします
$F_0$ は実数なので外部パラメータにすればいいのでかなりシンプルな実装になります
half vdotn = dot(i.view, i.normal.xyz);
half3 fresnel = (_F0 + (1.0h - _F0) * pow(1.0h - vdotn, 5)) * _Fresnel; // フレネル効果
環境光
フォン反射モデルの実装で環境光はパラメータで設定するようにしました
しかし、環境光はSkyboxや光源、周囲のオブジェクトによって複雑な計算が必要です
UnityのStandardシェーダーも環境光は直接計算していません
キューブマップやライトマップを使ったりします
↓↓unity Standardシェーダーに環境光が入っていない画像↓↓

Skyboxを元に簡易的に環境光を実装してみましょう
skyboxを反射光に反映
今回は特に式はありません
Schlickの近似式とSkyboxを合わせて疑似的に計算します
// 環境光
half4 refColor = UNITY_SAMPLE_TEXCUBE_LOD(unity_SpecCube0, reflect, 0);
half rim = pow(1.0 - abs(dot(i.view, i.normal)), 2);
float3 ambient = col.xyz * _Ka * float3(1,1,1) + refColor * rim * _RimPower;
これである程度空間に溶け込む物体シェーダーができました🎉
まとめ
自分の手でリアリティのあるシェーダーが作れました🎉
パラメータを変えることで色んな物体を表現できます
ただ、それぞれの設定パラメータが何を示しているのかわかりにくいことに気づきます
しかも物体の色や光源状況によって思った見え方にならず
1つの設定であらゆる状況に対応するシェーダーを用意するのが困難です
次回の物理ベースシェーディングではこの設定値の分かりにくさ、環境ごとの設定の難しさが解決されてる話をしようと思います(予定)
おまけ
ブリンフォン(Blinn-Phong)鏡面反射モデル
反射ベクトルは計算量が少し多い
代わりに、視線ベクトル+入射光ベクトルを正規化したハーフベクトルを用いるのがBlinn-Phong
ハーフベクトルと法線ベクトルの内積で鏡面反射を計算する
軽量な分、計算結果が粗くなっている
Lambertial diffuse BRDF
ランバート反射にエネルギー保存則を考慮したもの
Disney Diffuse BRDF
Lambertial diffuse BRDFにラフネスやフレネルなどの影響をいれたもの
エネルギー保存則は曖昧な実装になっているらしい
参考文献