作ったwebアプリについて(宣伝)
左右に表れる2つの本から1つを選ぶことを繰り返すことで, 新しい本に出逢えるwebアプリを作りました.
宣伝です.
↑web版
↑androidアプリ版
↑解説記事
このなかで, 出てくる本のラインナップを偏ったものにせず, 極力バラバラにするためにspectoral relaxationという手法を用いました.
この記事は「Novelty and Diversity in Top-N Recommendation -- Analysis and Evaluation」をベースに説明していきます.
よろしければ併せてどうぞ.
問題設定
リスト$\mathcal{I}$の要素$i$と$j$の間に距離$D_{ij}$が定められているとします.
そんなリスト$\mathcal{I}$から要素を$k$個取り出したい部分リスト${\mathcal{I}}{@k}$を作ったとします.
そのとき$\mathcal{I}_{@k}$内の要素間の距離$D$の合計や平均が大きくなるように, 部分リスト$\tilde{\mathcal{I}}
_{@k}$を作ることを考えます.
数式になおすと
\tilde{\mathcal{I}}
_{@k}=\mathrm{argmax}_{\mathcal{I}_{@k}} \sum_{i\in\mathcal{I}_{@k}}\sum_{j\in\mathcal{I}_{@k}} D_{ij}
という式になります.
これを愚直に解く場合, $_{|\mathcal{I}|}C_k$通りのパターンを計算する必要があります.
仮に100個のリストから10個の点を選ぶ場合でも$10^{13}$通りの計算量が必要なため, 大規模では計算できないです.
なので, 近似を使うことでこれを素早く計算していく手法を紹介します.
計算
ここで, $x_i$が↓を満たすベクトル$x$を作ることで式をかっこよくできます.
x_i=\begin{cases}1 & i\in\mathcal{I}_{@k} \\ 0 & i\notin\mathcal{I}_{@k}\end{cases}
\tilde{x}= \mathrm{argmax}_{|x|^2=k} x^TDx
ここで, 近似として$x$の値域を実数全体がとれるように拡張します.
その場合, 束縛条件($|x|^2=k$)下での値の最大化なのでラグランジュの未定乗数法で解くことができます.
0=\frac{\partial}{\partial x}\left\{
x^T D x-\lambda (x^T x - n)
\right\}
=2 (D-\lambda)x
よって, $\lambda$は行列$D$の固有値, $x$は行列$D$の固有ベクトルとみなせます.
$x$が行列$D$の固有ベクトルのとき, $x^T D x$は固有値となるため, 最大固有値に対応した固有ベクトルが$\tilde{x}$となります.
最後に, $\tilde{x}$の要素の大小関係からtop kを取得しリスト$\mathcal{I}_{@k}$を作れば完成です.
この計算手法を用いることで$|\mathcal{I}|^3$程度の計算量で各要素が離れたリストを作ることができました.
距離$D$の合計を小さくしたい場合は, 同様に考えることで, 最小固有値に対応した固有ベクトルを求めればOKです.
実験
実際にうまくいくのかシミュレーションで実験してみました.
条件としては, 二次元上にランダムに点をたくさんサンプリングし, $D_{ij}$を点$i$と点$j$の距離とします.
そして, 先程の手法で点を20個サンプリングしました.
# 標準正規分布に従って乱数を生成
N = 1000
rs = np.random.multivariate_normal([0,0], np.eye(2), N)
xs = rs[:,0]
ys = rs[:,1]
# 距離行列Dの作成
dx = xs.reshape((1,-1))-xs.reshape((-1,1))
dy = ys.reshape((1,-1))-ys.reshape((-1,1))
D = dx**2 + dy**2
# 最大固有値の固有ベクトル計算
e_vals, e_vecs = np.linalg.eigh(D)
itr = np.argmax(e_vals)
e_vec = e_vecs[:, itr]
# 値が大きい順にn個採用
# 固有ベクトルの符号的な問題から大きい順, 小さい順に20個点をとりその比較をした
n = 20
points_plus = np.argsort(e_vec)[:20]
points_minus = np.argsort(e_vec)[-20:]
if np.mean(D[points_plus,:][:,points_plus]) > np.mean(D[points_minus,:][:,points_minus]):
points = points_plus
else:
points = points_minus
その結果が↓
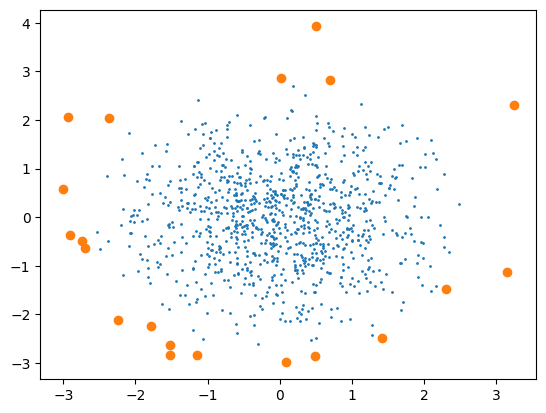
ちゃんと点同士の距離が遠くなっていることが確認できました

たくさん実験してみました
横軸が粒子間の平均距離です.
青のデータがランダムに20個の点を選んだ場合.
オレンジのデータが先程の手法で点を選んだ場合です.
オレンジのデータのほうが平均距離が長いことが確かめられます.
[おまけ]ラグランジュの未定乗数法について
ある条件$g(x)=0$下での$f(x)$を最大化・最小化させる点$\tilde{x}$は
\partial_x \{f(x)-\lambda g(x)\}=0
を満たすことが知られています.
ここででてくる$\lambda $のことをラグランジュの未定乗数と呼びます.