概要
皆さん, アキネーターというゲームはご存知でしょうか.
特定の人物を, 質問から当てるゲームです.
やったことある人はわかると思うのですが, 何回かの質問で目的の答えまでたどり着けるのはすごいですよね.
そんなアキネーターなのですが内部のアルゴリズムは秘密となっているそうです.
面白そうなので, 内部のアルゴリズムを妄想し, 実際に組んでみました!!
題材としては, 種類の多くデータのまとまっているポケモンをターゲットにしました.
よければ遊んでやってください
アルゴリズム編と実装編の2つを予定しています.
問題設定
まずはじめに, ユーザー回答$a$は「はい」「だいたいそう」「わからない」「たぶんちがう」「ちがう」の5種類あります.
これにそれぞれ「+1」「+1/2」「0」「-1/2」「-1」という数字を割り当てます(ここはあとで活きてきます).
また, この数字の集合を$\mathcal{A}$とします.
また, $n$回目の質疑応答時のユーザー回答を$a_n$に, $n$回目までの質疑応答時のユーザー回答のログを$A_n$にします.
\begin{align}
a_n &\in \mathcal{A}=\left\{1,\frac{1}{2},0,-\frac{1}{2},-1\right\}
\\
A_n &=(a_1,a_2,\cdots a_n)
\end{align}
同様に質問$q$についても整理しましょう.
全質問の集合を$\mathcal{Q}$, $n$回目の質問を$q_n$に, それまでの質問のログを$Q_n$にします.
\begin{align}
q_n &\in \mathcal{Q}
\\
Q_n &=(q_1,q_2,\cdots q_n)
\end{align}
このとき,
- $n$回目の質疑応答が終わり$Q_n,A_n$がわかった際の, ポケモン$i$の確率分布$p(i|Q_n,A_n)$
- $n-1$回目の質疑応答が終わった際に, 次の質問$q_n$はどれを選ぶべきか
が分かれば嬉しいです.
一般的な場合について
ユーザー回答の分布p(a|q,i)について
答え$a_n$の条件付き確率である, $p(a_n|Q_n,A_{n-1},i)$は過去の質疑応答の内容$Q_{n-1},A_{n-1}$に依存しないことが予想できます.
なので
\begin{align}
p(a_n|Q_n,A_{n-1},i) &= p(a_n|q_n,i)
\end{align}
が成り立ちます.
この$p(a_n|q_n,i)$が
\begin{align}
p(a|q,i)
&=
\frac{
\exp \{-\beta (a-\alpha_{q,i})^2\}
}{
\sum_{a'\in \mathcal{A}} \exp \{-\beta (a'-\alpha_{q,i})^2\}
}
\end{align}
に従うとしましょう.
ここで, $\alpha_{q,i}$は実際のポケモンの状態を表します.
具体的には$q=(赤色ですか?)$で$i=(ヒトカゲ)$なら$\alpha_{q,i}=1$となります.
なのでこの数式は, 回答$a$が実際の答えである$\alpha_{q,i}$に近いほど確率が大きくなるsoftmax関数とみなせます.
$\beta$はどれだけ誤りを許容するかの目安であり, $\beta=\infty$で正解以外の値が0になり, $\beta=0$で分布が一様分布になります.
実際に$\beta=\alpha=1$のグラフを↓に示します.
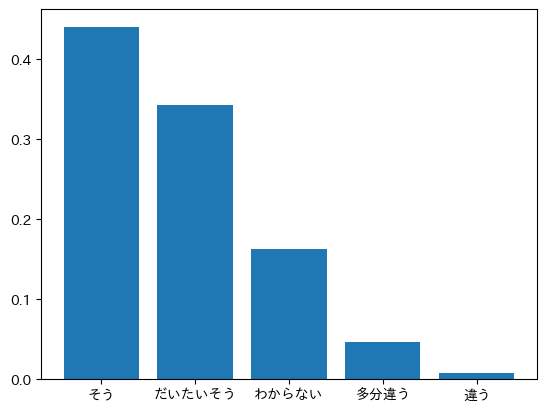
ポケモンiの分布p(i|Q_n,A_n)について
一個目の課題である「$n$回目の質疑応答が終わり$Q_n,A_n$がわかった際の, ポケモン$i$の確率分布$p(i|Q_n,A_n)$」にアプローチするため, ポケモンiの分布$p(i|Q_n,A_n)$について考えていきます
ポケモンiの分布$p(i|Q_n,A_n)$は$i$に依存するところのみ抜き出すと,
\begin{align}
p(i|Q_n,A_n)
&=\frac{p(a_n|Q_n,A_{n-1},i)p(i|Q_{n-1},A_{n-1})}{p(a_n|Q_n,A_{n-1})}
\\&=\frac{p(a_n|q_n,i)p(i|Q_{n-1},A_{n-1})}{p(a_n|Q_n,A_{n-1})}
\\&\propto p(a_n|q_n,i)p(i|Q_{n-1},A_{n-1})
\end{align}
となります.
まずはじめにベイズの定理を使い, 式を展開したあとに, $p(a|q,i)$に書き換えました.
この式と$\sum_i p(i|Q_n,A_n)=1$から$p(i|Q_n,A_n)$の更新方程式
\begin{align}
p(i|Q_n,A_n) = \frac{ p(a_n|q_n,i)p(i|Q_{n-1},A_{n-1}) }{ \sum_i p(a_n|q_n,i)p(i|Q_{n-1},A_{n-1}) }
\end{align}
が導けます.
なので, 漸化的に$p(i|Q_n,A_n)$が求まります.
一個目の課題である「$n$回目の質疑応答が終わり$Q_n,A_n$がわかった際の, ポケモン$i$の確率分布$p(i|Q_n,A_n)$」はクリアです.
質問q_nはどれを選ぶべきか
二個目の課題である「$n-1$回目の質疑応答が終わった際に, 次の質問$q_n$はどれを選ぶべきか」にアプローチしましょう.
そのために, まず相互情報量について考えます.
相互情報量とは, ある分布の情報が与えられたとき, もう片方の分布のエントロピーがどれくらい変わるかの指標です.
そのため,今回のケースではポケモン$i$とユーザー回答$a$の相互情報量を最大化することが筋が良さそうです.
\begin{align}
q_n &=\mathrm{argmax}_{q_n\in \mathcal{Q}} I(i;a|Q_n,A_{n-1})
\\
&= \mathrm{argmax}_{q_n\in \mathcal{Q}} -\sum_i p(i|Q_n,A_{n-1})\log p(i|Q_n,A_{n-1})+\sum_{i,a_n} p(i,a_n|Q_{n},A_{n-1})\log p(i|Q_{n},A_{n})
\end{align}
一式目から二式目で相互情報量は条件付きエントロピーと同時エントロピーの差でかけることを用いました.
ここで, $p(i|Q_n,A_{n-1}) = p(i|Q_{n-1},A_{n-1})$が成り立つ(※おまけ①参照)
そのため, 上式の第一項は$q_n$によらない形になるので無視して大丈夫です.
\begin{align}
q_n
&= \mathrm{argmax}_{q_n\in \mathcal{Q}} \sum_{i,a_n} p(i,a_n|Q_{n},A_{n-1})\log p(i|Q_{n},A_{n})
\end{align}
この式を変形すると
\begin{align}
q_n^*
&=
\mathrm{argmax}_{q_n\in \mathcal{Q}} \sum_{i,a_n} p(i,a_n|Q_{n},A_{n-1})\log p(i|Q_{n},A_{n})
\\&=
\mathrm{argmax}_{q_n\in \mathcal{Q}} \sum_{i,a_n} p(i|Q_{n},A_{n})p(a_n|Q_n,A_{n-1})\log p(i|Q_{n},A_{n})
\\&=
\mathrm{argmax}_{q_n\in \mathcal{Q}}\sum_{a_n} p(a_n|Q_n,A_{n-1})\sum_i p(i|Q_{n},A_{n})\log p(i|Q_{n},A_{n})
\\&=
\mathrm{argmax}_{q_n\in \mathcal{Q}} \sum_{a_n,i} p(a_n|q_n,i)p(i|Q_{n-1},A_{n-1})\\
&\times\{\log p(a_n|q_n,i) + \log p(i|Q_{n-1},A_{n-1}) - \log p(a_n|Q_n,A_{n-1})\}
\end{align}
となります.
ここで{…}内の第1項,第2項,第3項についてそれぞれ考えると.
\begin{align}
(第1項)&=\sum_{a_n,i}p(a_n|q_n,i)p(i|Q_{n-1},A_{n-1})\log p(a_n|q_n,i)
\\&=-\sum_i p(i|Q_{n-1},A_{n-1}) \{ -\sum_a p(a|q_n,i)\log p(a|q_n,i)\}
\end{align}
\begin{align}
(第2項)&=\sum_{a_n,i}p(a_n|q_n,i)p(i|Q_{n-1},A_{n-1})\log p(i|Q_{n-1},A_{n-1})
\\&= \sum_i p(i|Q_{n-1},A_{n-1})\log p(i|Q_{n-1},A_{n-1}) \sum_a p(a|q_n,i)
\\&= \sum_i p(i|Q_{n-1},A_{n-1})\log p(i|Q_{n-1},A_{n-1})
\end{align}
\begin{align}
(第3項)&=-\sum_{a_n,i}p(a_n|q_n,i)p(i|Q_{n-1},A_{n-1})\log p(a_n|Q_n,A_{n-1})
\\&= -\sum_{a_n,i}p(a_n|q_n,i)p(i|Q_{n-1},A_{n-1})\log \sum_{i'} p(a_n,i'|Q_n,A_{n-1})
\\&= -\sum_{a_n,i}p(a_n|q_n,i)p(i|Q_{n-1},A_{n-1})\log \sum_{i'} p(a_n|Q_n,A_{n-1},i')p(i'|Q_{n},A_{n-1})
\\&= -\sum_{a_n,i}p(a_n|q_n,i)p(i|Q_{n-1},A_{n-1})\log \sum_{i'} p(a_n|Q_n,A_{n-1},i')p(i'|Q_{n-1},A_{n-1})
\\&=-\sum_{a_n,i}p(a_n|q_n,i)p(i|Q_{n-1},A_{n-1})\log \sum_{i'} p(a_n|q_n,i')p(i'|Q_{n-1},A_{n-1})
\\&=-\sum_a \{\sum_i p(a|q_n,i)p(i|Q_{n-1},A_{n-1})\}\times \{\log \sum_i p(a|q_n,i)p(i|Q_{n-1},A_{n-1})\}
\end{align}
となります.
式をきれいにするために$x$に対するシャノンエントロピーを求める汎関数を$H_x$を導入します.
\begin{align}
H_x[p(x)]&=-\sum_x p(x)\log p(x)
\end{align}
そうすると, 最終的な標識は
\begin{align}
q_n &= \mathrm{argmax}_{q_n}
-\sum_i p(i|Q_{n-1},A_{n-1})H_a[p(a|q_n,i)]
+H_a[\sum_i p(a|q_n,i)p(i|Q_{n-1},A_{n-1})]
\end{align}
となります.
ここで, (第2項)は$q_n$に依らないため除外をしました.
$p(a|q_n,i)$は「ユーザー回答の分布p(a|q,i)について」の節で,
$p(i|Q_{n-1},A_{n-1})]$は「ポケモンiの分布p(i|Q_n,A_n)について」の節で求めました.
したがって, $q_n$を計算する式が求まるため, 二個目の課題である「$n-1$回目の質疑応答が終わった際に, 次の質問$q_n$はどれを選ぶべきか」もクリアです.
まとめ
一旦, 出てきた数式をまとめます
そうすると, 最終的な標識は
\begin{align}
p(a|q,i)
&=
\frac{
\exp \{-\beta (a-\alpha_{q,i})^2\}
}{
\sum_{a'\in \mathcal{A}} \exp \{-\beta (a'-\alpha_{q,i})^2\}
}
\\
p(i|Q_n,A_n) &= \frac{ p(a_n|q_n,i)p(i|Q_{n-1},A_{n-1}) }{ \sum_i p(a_n|q_n,i)p(i|Q_{n-1},A_{n-1}) }
\\
q_n &= \mathrm{argmax}_{q} -\sum_i p(i|Q_{n-1},A_{n-1})H_a[p(a|q,i)]+H_a[\sum_i p(a|q_n,i)p(i|Q_{n-1},A_{n-1})]
\\
H_x[p(x)]&=-\sum_x p(x)\log p(x)
\end{align}
となります.
この式のままだと, 抽象的で実装しづらそうです.
次の章ではこの式を更に簡単にしていきます.
実際の状態α_{q,i}の絶対値が1の場合
実際の状態が, イエス or ノーしかとらずハッキリしている状況を考えます.
そのとき, $\alpha_{q,i}$は「はい」である「+1」か「いいえ」である「-1」しか取らなくなります.
ユーザー回答の分布p(a|q,i)について
$\mathcal{A}={-1,-1/2,0,1/2,1}$は0周りで対称です.
なので$p(a|q,i)$の規格化定数の$ \sum_{a'\in \mathcal{A}} \exp {-\beta (a'-\alpha_{q,i})^2}$は$\alpha_{q,i}$の絶対値にのみ依存します.
したがって規格化定数は$\alpha_{q,i}=\pm 1$の場合, 定数とみなしてOKです.
\begin{align}
&\sum_{a'\in \mathcal{A}} \exp \{-\beta (a'-\alpha_{q,i})^2\}
\\&=
\exp(-\beta\cdot 0)
+
\exp(-\beta\cdot 1/4)
+
\exp(-\beta\cdot 1)
+
\exp(-\beta\cdot 9/4)
+
\exp(-\beta\cdot 4)
\\& \equiv C
\end{align}
\begin{align}
p(a|q,i)
&=
\frac{
\exp \{-\beta (a-\alpha_{q,i})^2\}
}{
\sum_{a'\in \mathcal{A}} \exp \{-\beta (a'-\alpha_{q,i})^2\}
}
\\&=
\frac{
\exp \{-\beta (a-\alpha_{q,i})^2\}
}{
C
}
\\&\propto \exp \{-\beta (a-\alpha_{q,i})^2\}
\end{align}
ポケモンiの分布p(i|Q_n,A_n)について
$p(i|Q_n,A_n)$は先程の式から,
\begin{align}
p(i|Q_n,A_n)
&\propto
p(a_n|q_n,i)p(i|Q_{n-1},A_{n-1})
\\&\propto
\exp \{-\beta (a_n-\alpha_{q_n,i})^2\} p(i|Q_{n-1},A_{n-1})
\end{align}
に変形できます.
この式を漸化的にとくと
\begin{align}
p(i|Q_n,A_n)
&\propto
\exp \{-\beta (a_n-\alpha_{q_n,i})^2\} p(i|Q_{n-1},A_{n-1})
\\&\propto
\exp \{-\beta (a_n-\alpha_{q_n,i})^2-\beta (a_{n-1}-\alpha_{q_{n-1},i})^2\} p(i|Q_{n-2},A_{n-2})
\\&\cdots
\\&\propto
\exp \{-\beta \sum_{a,q\in (A_n,Q_n)}(a-\alpha_{q,i})^2\}
\end{align}
これと, $\sum_i p(i|Q_n,A_n)=1$から
\begin{align}
p(i|Q_n,A_n) &=\frac{
\exp(-\beta \mathcal{H}_{i,n})
}{
\sum_i \exp (-\beta \mathcal{H}_{i,n})
}
\\
\mathcal{H}_{i,n}&=\sum_{a,q\in (A_n,Q_n)} (a-\alpha_{q,i})^2
\end{align}
が算出できます.
$ \mathcal{H}_{i,n}$は更新方程式の形に書き直すと
\begin{align}
\mathcal{H}_{i,n}&=(a_n-\alpha_{q_n,i})^2 + \mathcal{H}_{i,n}
\end{align}
となります.
質問q_nはどれを選ぶべきか
復習のため$q_n$を求める数式を再度掲載します.
\begin{align}
q_n &= \mathrm{argmax}_{q_n}
-\sum_i p(i|Q_{n-1},A_{n-1})H_a[p(a|q_n,i)]
+H_a[\sum_i p(a|q_n,i)p(i|Q_{n-1},A_{n-1})]
\end{align}
この式の第一項は$\mathcal{A}$の対称性から$\alpha_{q,i}$の絶対値のみで決定します.
よって, $\alpha_{q,i}=\pm 1$しか取らない場合は, 第一項は定数とみなしてOKです.
この場合,
\begin{align}
q_n &= \mathrm{argmax}_{q_n}
H_a[\sum_i p(a|q_n,i)p(i|Q_{n-1},A_{n-1})]
\end{align}
となります.
さてここで,$C$を正の定数としたとき, $ \mathrm{argmax} H_x[ Cp(x) ]=\mathrm{argmax}H_x[ p(x) ]$が成り立ちます(※おまけ②参照)
それを用いると, $p(a|q_n,i)$や$p(i|Q_{n-1},A_{n-1})$の規格化定数は無視できます.
\begin{align}
p(a|q_n,i) & \propto \exp \{-\beta (a-\alpha_{q,i})^2\}
\\
p(i|Q_{n-1},A_{n-1}) & \propto \exp(-\beta \mathcal{H}_{i,n})
\end{align}
を思い出すと
\begin{align}
q_n &= \mathrm{argmax}_{q} H_a\left[\sum_i \exp\{-\beta(a-\alpha_{q,i})^2-\beta \mathcal{H}_{i,{n-1}}\}\right]
\end{align}
が成立します.
まとめ
再び, 最終的な標識をまとめましょう
\begin{align}
p(i|Q_n,A_n) &=\frac{
\exp(-\beta \mathcal{H}_{i,n})
}{
\sum_i \exp (-\beta \mathcal{H}_{i,n})
}
\\
\mathcal{H}_{i,n}&=(a_n-\alpha_{q_n,i})^2 + \mathcal{H}_{i,n}
\\
q_n &= \mathrm{argmax}_{q} H_a\left[\sum_i \exp\{-\beta(a-\alpha_{q,i})^2-\beta \mathcal{H}_{i,{n-1}}\}\right]
\\
H_x[p(x)]&=-\sum_x p(x)\log p(x)
\end{align}
かなりキレイな形になりました.
「これなら実装できそう」と思えてきたのではないでしょうか.
おまけ
おまけ①p(i|Q_n,A_{n-1}) = p(i|Q_{n-1},A_{n-1})が成り立つわけ
\begin{align}
q_n &= \mathrm{argmax}_{q} I(i;a)
\end{align}
で決定論的に$q_n$を定めたとします.
このとき, $p(q_n|Q_{n-1},A_{n-1},i)$は
\begin{align}
p(q_n|A_{n-1},Q_{n-1},i)=\begin{cases}
1 & q=\mathrm{argmax}_{q} I(i;a))\\
0 & q\neq\mathrm{argmax}_{q} I(i;a)
\end{cases}
\end{align}
となります.
このとき, 左辺は$i$の関数である一方, 右辺は$i$の関数ではないため,
\begin{align}
p(q_n|A_{n-1},Q_{n-1},i)=p(q_n|A_{n-1},Q_{n-1})
\end{align}
が成り立ちます.
よって, $i$と$q_n$は条件付き独立
\begin{align}
q_n \perp i \ | \ A_{n-1},Q_{n-1}
\end{align}
が成立します.
したがって
\begin{align}
p(i|Q_n,A_{n-1})=p(i|Q_{n-1},A_{n-1})
\end{align}
が成り立ちます.
おまけ②argmax H_x[ Cp(x) ]=argmax H_x[ p(x) ]が成り立つわけ
\begin{align}
\mathrm{argmax} H_x[ Cp(x) ]&=\mathrm{argmax} \{-C\sum_x p(x)\log p(x)+C\log C\cdot \sum_x p(x)\}
\\&=\mathrm{argmax} \{-C\sum_x p(x)\log p(x)+C\log C\cdot 1\}
\\&=\mathrm{argmax} \{CH_x[p(x)]\}
\\&=\mathrm{argmax} H_x[ p(x) ]
\end{align}