はじめに
ビームサーチ(Beam Search)は貪欲法の高速性と全探索の正確性にトレードオフを持たせたヒューリスティック探索手法としてよく知られています。主に文章生成や機械翻訳の分野で活躍している他、私の所属する競技プログラミングの界隈においてもヒューリスティック系コンテストでよく利用されます。一方で、探索アルゴリズムの研究分野においては、ビームサーチの探索方法を変換してより高性能な探索アルゴリズムを生み出そうとする動きも見られます。本記事では、ビームサーチを変換したアルゴリズムの1つであるビームスタックサーチ(Beam-Stack Search)を解説します。ビームスタックサーチとは何者かを簡単に言うとビームサーチを最適解の発見を保証できる形に変換したものと言えます。以下では、まずビームサーチの提案論文を紹介し、当論文を読んでの私見を述べ、最後にビームスタックサーチのアルゴリズムを解説します。
論文情報
- タイトル:Beam-Stack Search: Integrating Backtracking with Beam Search
- 著者/所属:Rong Zhou and Eric A. Hansen / Department of Computer Science and Engineering Mississippi State University
- 出版元:ICAPS'05: Proceedings of the Fifteenth International Conference on International Conference on Automated Planning and Scheduling
- 被引用数: 155(2022/5/6 時点)
ビームスタックサーチは上記の論文で提案されました。アルゴリズム分野における主要国際会議の1つである ICAPS に採択されており被引用数が多い部類の論文です。しかし、ザッと調べた所感では応用としての引用は少なく他の探索アルゴリズムの提案論文からの引用が多い印象でした。このことから、ビームサーチほど実践的なアルゴリズムではないと推測されます。
論文概要
- ビームサーチを最適解の発見が保証されるように変換したアルゴリズム(命名:ビームスタックサーチ; Beam-Stack Search)を提案する。
- これはビームサーチに beam stack というデータ構造を導入しバックトラックを可能にしたものである。
- ビームスタックサーチは高速に良質な解を発見し最終的には最適解に収束する。
- メモリ効率の良い実装である分割統治版のアルゴリズム Divide-and-Conquer Beam-Stack Search も提案する。
- STRIPS と呼ばれる Planning 問題のベンチマークで評価し優位性を示した。
※下2点は解説の対象外ですので当論文を参照してください。ちなみに分割統治版については論文内でさらに他の論文に参照が入ります(ぇ
私見
ビームスタックサーチは実践的なアルゴリズムではないと推測されると前述しましたが、実際、当論文を読み終えた私の視点でも、最適でなくてよいから良質な解を得たい場面ならビームサーチを差し置いてビームスタックサーチを適用したい場面は極少数だろうと感じました。また、最適解を求めたい場面でも他のソルバーに軍配が上がる場合が多いんじゃないかなーと思います。
論文概要で『ビームスタックサーチはビームサーチの変形である』と述べられていますが、アルゴリズムを把握した上で私見を述べると、『ビームスタックサーチは分枝限定法にビームを導入したものである』と理解した方がアルゴリズムの直感に合っています。そもそも最適性を保証する探索アルゴリズムなので、ビームサーチの側から理解しようとするのは筋が悪そうです。ただ、界隈における研究の流れとしてはビームサーチの変形であると述べるのが正しいのだとは思います。
ビームスタックサーチのアルゴリズム
今、ある目的関数 $g$ を最小化する問題 $P$ を扱っていると仮定しましょう。また、問題 $P$ の探索空間は1つの根付き木で表現され、葉ノードはすべて同じ深さ $d$ に存在し、各葉ノードが1つの実行可能解に対応するとします。さらに、中間ノードも含めた各ノード $n$ に対して $g(n) \geq 0$ が計算可能であることも仮定します。
ビームスタックサーチはヒューリスティック関数 $h$ を必要とし、$h$ は各ノード $n$ の子孫で最良の実行可能解 $ n^* $ の下界 $f(n) = g(n) + h(n) \leq g( n^* )$ の計算に利用されます。すなわち、分枝限定法のように、$n$ からどう頑張っても $f(n)$ より目的関数値を小さくできないという情報を得られなければビームスタックサーチは機能しません。
ビームスタックサーチは、初めの $d$ ステップのみビームサーチとほぼ同じ動作でノードを展開します。その後、beam stack と呼ばれるデータ構造を用いたバックトラックにより、下界 $f$ および上界(暫定解)を利用した広範な枝刈りを行うことが特徴です。
ノードの展開と beam stack
ビームスタックサーチにはビームサーチと同様にビーム幅 $W$ がパラメータとして存在します。これは、探索の各ステップにおいて $f$ に関する上位 $W$ 個のノードのみを探索対象とすることを表します。
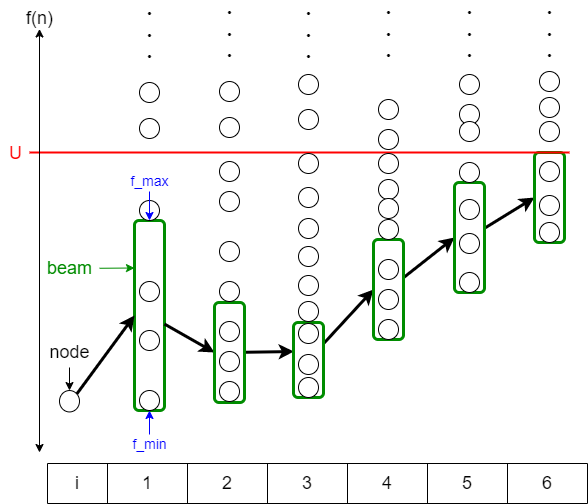
ここで、ビームスタックサーチ特有のデータ構造 beam stack を導入します。データ構造と言われるとなんとなく大層なものを想像してしまいますが、探索の深さ $i \in \{1, 2, \ldots, d\}$ ごとに $f$ に関する半開区間 $[f^i_{\mathrm{min}}, f^i_{\mathrm{max}})$ を push/pop する、あるいは先頭の要素を更新するだけのただのスタックです。
beam stack が保持する値はノードの展開に影響を与えます。具体的には、深さ $i$ に対して $[f^i_{\mathrm{min}}, f^i_{\mathrm{max}})$ であってノード $n$ の展開を試みるとき、$f^i_{\mathrm{min}} \leq f(n) < f^i_{\mathrm{max}}$ を満たす場合のみ展開を許すというものです。このとき、探索の初期段階ではスタックに値が無いため、 $[0, \infty)$ あるいは既知の上界 $U$ に対して $[0, U)$ を取ることにします。
beam stack の先頭要素は、対応する深さの展開が完了すると同時に更新されます。展開後、探索対象に選ばれた上位 $W$ 個のノードにおける $f$ の最小値を $f^i_{\mathrm{min}}$ とし、ぎりぎり選ばれなかった $W+1$ 位のノードにおける $f$ を $f^i_{\mathrm{max}}$ とするだけです。そもそも展開されたノードの数が $W$ 個を超えなかった場合は $f^i_{\mathrm{max}}$ の更新は不要です。
$W=3$ および $d=6$ の場合、ノードの展開と beam stack の様子は下図のようになります。なお、ノード間の枝まで図示すると煩雑になるのでそれは無視しています。
上記の操作を一度なぞるだけだとビームサーチとほぼ同等の動作になっていることがわかります。ここからがビームスタックサーチの本番です。
バックトラック
深さ $d$ の展開を行ったとき、新たな実行可能解を得たことになり、目的関数値の上界 $U$ が更新されます。ビームスタックサーチの特徴は、更新された $U$ と beam stack を利用したバックトラックにより、広範な枝刈りを行うことにあります。
バックトラックでは beam stack の先頭要素が $f^i_{\mathrm{max}} < U$ を満たす深さ $i$ まで探索を戻し、beam stack から要素を pop します。さらに、beam stack の先頭要素を $f^i_{\mathrm{min}} \leftarrow f^i_{\mathrm{max}}$ および $f^i_{\mathrm{max}} \leftarrow U$ と更新し、展開されるノードの範囲をスライドします。この結果、元の $[f^i_{\mathrm{min}}, f^i_{\mathrm{max}})$ で展開される子孫をすべて枝刈りしたことになります。
このような大胆な枝刈りの妥当性は次の2点から明確です。(1) $j > i$ について $f^j_{\mathrm{max}} \geq U$ であることから、深さ $i+1$ 以降で探索対象とならなかったノードからは、目的関数値が $U$ より良い解を得られません。(2) 深さ $i$ 以降で探索対象となったノードは二度と展開する必要はありません。
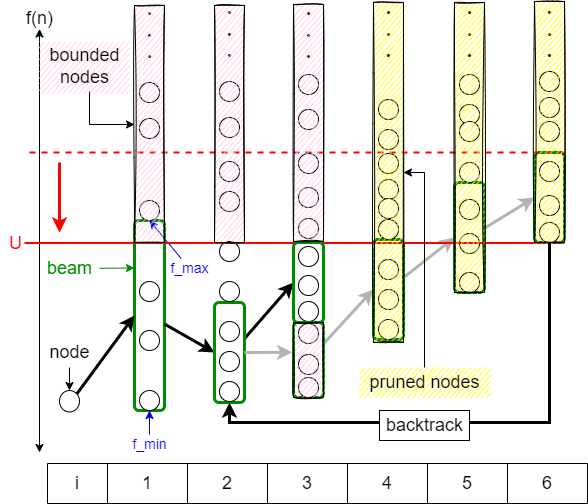
また、上界が改善されることにより展開されるノードの数も減るため、実質的に枝刈りされるノードの数はさらに多いです。ビームスタックサーチは、このような大規模なバックトラックおよび枝刈りと、戻ってきた深さからのノードの再展開を繰り返します。バックトラックも含めた探索の様子は下図のようになります。
以上の説明から、beam stack が空になった時、ビームスタックサーチは最適解を見つけており、そのときの $U$ が最適値に対応するということもわかります。このように、ビームスタックサーチはビームサーチと同等の動作から開始するため高速に良質な解にたどり着き、分枝限定により解の質を高めつつ、最終的には最適解に収束するアルゴリズムなのです。
注意点として、ビームスタックサーチはメモリ消費量をビームサーチと同等に抑えるために、走査したノードを記憶しておくようなキャッシュ機能は持ちません。すると、どうしても以前に走査したことがあるノードを再度走査してしまう場面が出てきます。これは大きなオーバーヘッドであり、ビームスタックサーチが実践的なアルゴリズムではないと推測される要因の1つです。最適でなくてよいから良質な解が欲しいという場面では、単純にビーム幅を大きく取ったビームサーチで足りることが多そうです。マシンのメモリがあまりにも少ないとかであれば話は別かもしれませんが。
おわりに
競技プログラミング界隈では、chokudai さんが独自に開発したビームサーチの亜種である chokudai サーチ が、ビームスタックサーチあるいはその亜種なのではないかと言われることがありましたが、この解説記事をもって明確に 『chokudai サーチはビームスタックサーチやその亜種ではない』 と言えるかと思います。また、本記事で紹介した論文および関連論文から、chokudai サーチと等価なアルゴリズムにたどり着けないかと少しだけ期待しましたが、今のところ 『chokudai サーチは独自のアルゴリズムである可能性が高い』 という見解です。(2022/5/6時点)
……という気持ちと chokudai サーチを褒める呟きを Twitter で垂れ流していたところ、chokudai さんから「論文化まってます!!!」と無邪気に引用RTされたので、研究者の端くれとして片手間ですが chokudai サーチの論文化を検討していきたいと思います(ふぇぇ)。私はビームサーチ界隈に秀でてはいないので、良いベンチマークや有名な関連論文を知っている方はぜひ教えてください。