はじめに
Houdiniでは様々なシミュレーションのSolverが用意されています。
Rigid Body Solver、POP Solver、Vellum Solver、Pyro Solver...などなど。
これらのSolverの中に入っていくとわかりますが、そのほとんどもノードの組み合わせで成り立っています。
つまり、自分でもシミュレーションのSolverを作れるということです。
ということで、今回は簡単なシミュレーションのSolverを作成していきます。
SolverSOPを使ってしまえば済む話ですね
今回の目的
- 簡単なシミュレーションのSolverをDOPで実装する
- DOPの理解を深める
大まかな流れ
DOP上でシミュレーションを実装する大まかな流れとしては、以下のようになります。
- シミュレーションオブジェクト作成
- Solver作成
- その他設定
1ではDOP内でオブジェクトを作成し、シミュレーションを行う対象のジオメトリやその物性値を設定します。
2では毎ステップ計算を行うSolver部分を作成し、物体が移動・変形できるようにします。
3では重力や風などシミュレーション全体に影響を与える力や、衝突判定を行う物体を設定します。
SOPでの準備
はじめにシミュレーションを行うシーンを適当に作ります。
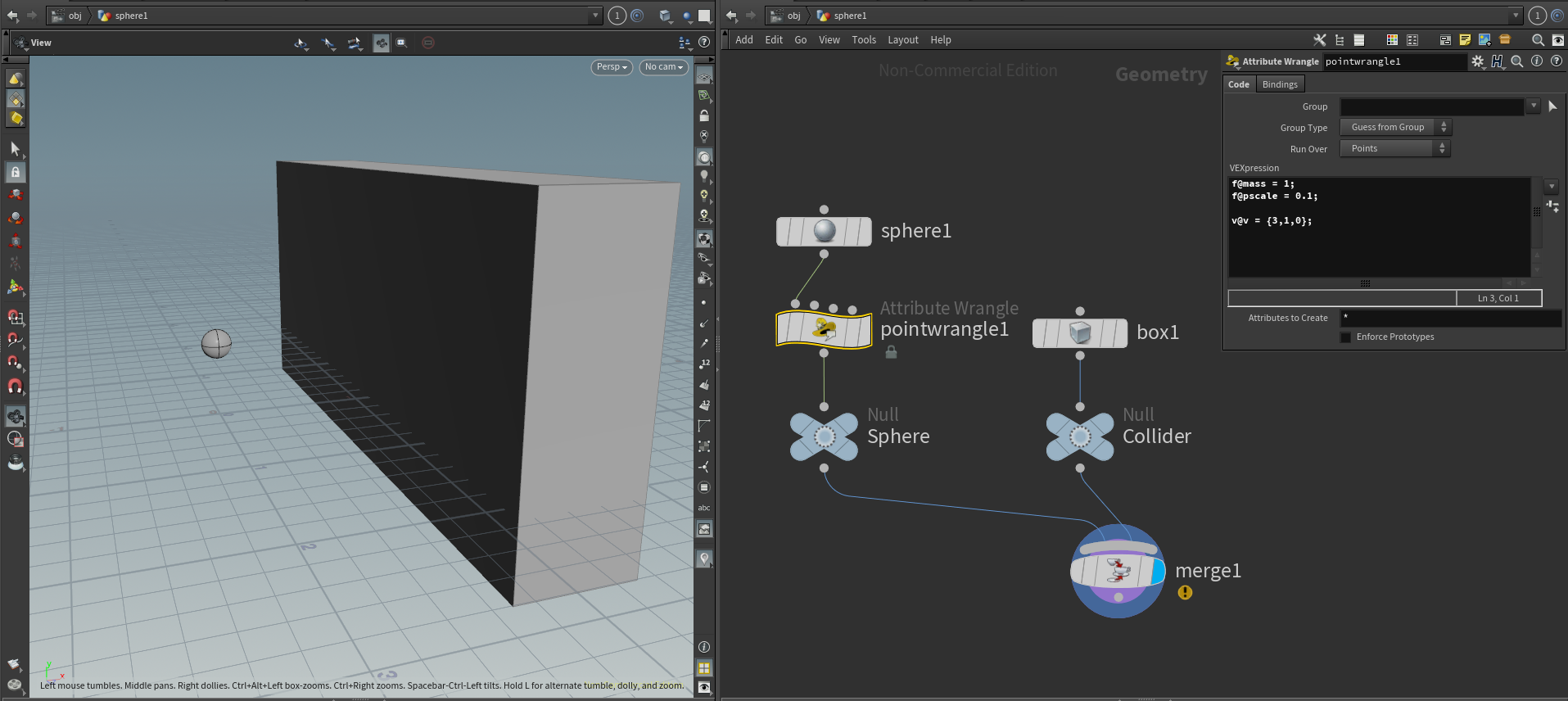
箱とそれに衝突する球を用意し、球には質量と直径、初速を設定しています。
そしてDOP Networkを作成し、以降その内部で操作していきます。
シミュレーションオブジェクト作成
すでに実装されているシミュレーションのObject DOP (FlipObject、SmokeObject、POPObject...など)の中に入ってみるとわかりますが、やっていることはどれも変わらず、
- EmptyObjectDOPを作成
- SOPからジオメトリデータを読み込み
- 必要な物性値を設定
となります。
これらを踏まえると、ノードは以下のようになります。
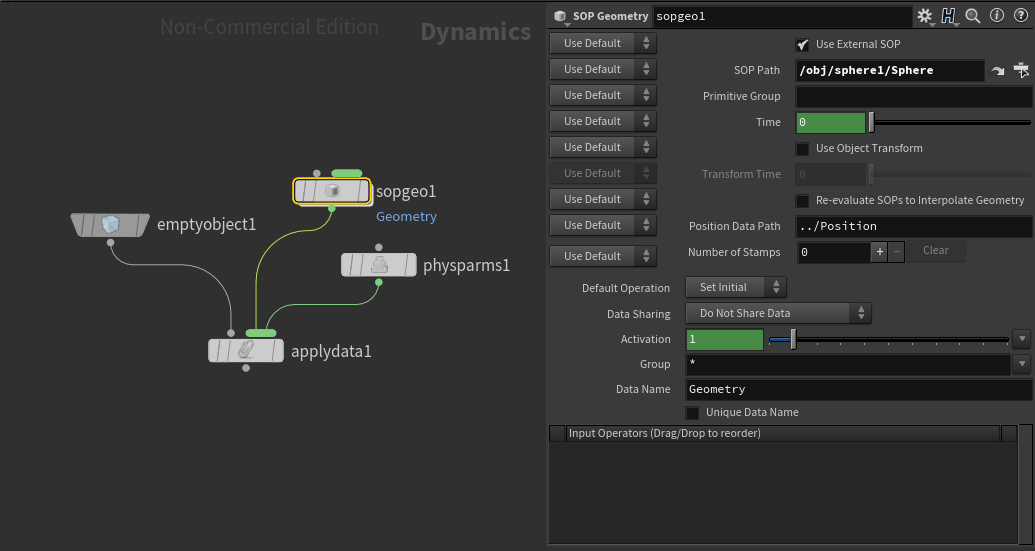
EmptyObjectにジオメトリと物性値のデータをApplyDataDOPを使って設定しています。
SOPGeometryDOPのSOP Pathにはジオメトリのパスを入れ、PhysicalParametersDOPでは適当な物性値を入力します。
今回は、ジオメトリのパスには先ほどSOPで用意した球を、物性値ではFrictionを0.2に設定しました。
以上でシミュレーションオブジェクトは完成です。
ちなみに、DOPにおいて灰色の線はオブジェクトとデータ、緑色の線はデータを受け渡ししていることを示しているそうです。
Solver作成
オイラー法を使った簡単なシミュレーションのSolverを組んでいきます。
オイラー法というと難しいように聞こえますが、簡単に言えば、力で速度を更新し、速度で位置を更新する方法です。
ノードは以下のようになります。
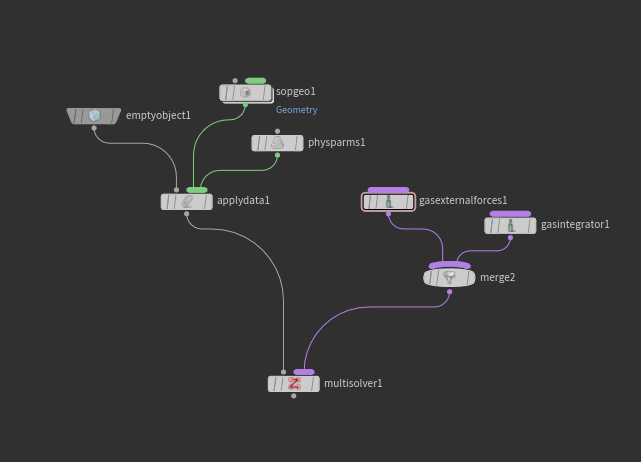
先ほど作ったオブジェクトをMultiSolverDOPの左に入力し、
GasExternalForcesDOPとGasIntegratorDOPをMergeしてMultiSolverDOPの右に入力しています。
ここで、GasExternalForcesDOPではオブジェクトに影響している外力で速度を更新しています。
外力が影響するのはSOPGeometryDOPで設定したジオメトリなので、Geometryパラメータにはそのジオメトリの名前を入力します。

また、GasIntegratorDOPでは速度をもとに位置を更新しています。
このとき、球の直径@pscaleを考慮した衝突処理を行いたいので、Use Pscale for SDFにチェックを入れておきます。
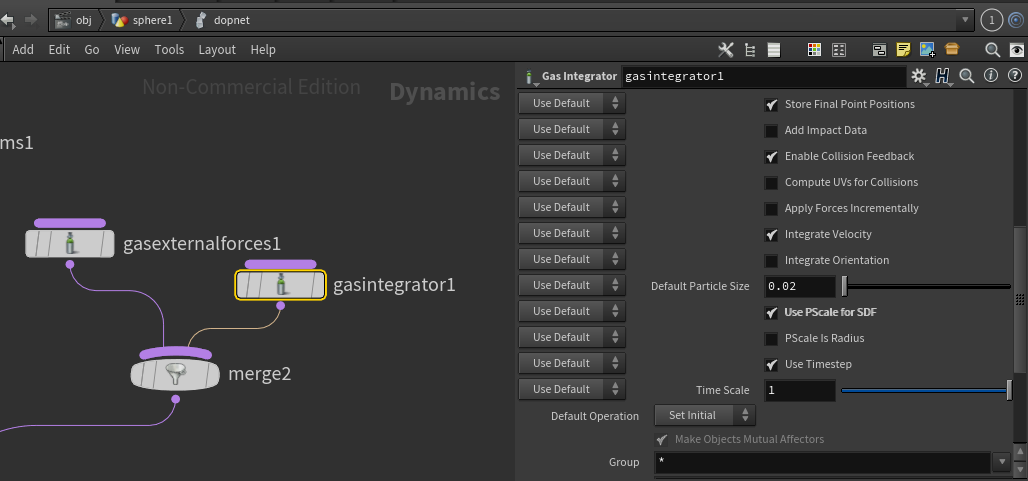
以上でSolverも完成です。
その他設定
最後にGroundPlaneやStaticObject、Gravityを追加し、完成です。
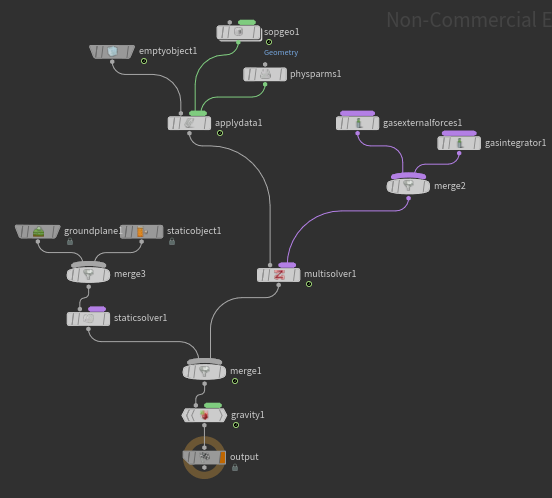
結果
球が壁に衝突して、跳ねる様子をシミュレーションすることができました。
球と壁の衝突判定やその処理はGasIntegratorDOPが行っているため、簡単にできました。
応用(シンプレクティック法)
応用として、シンプレクティック法のソルバーを実装します。
シンプレクティック法については書ききれないので、ネットや本で調べてみてください。
ざっくり言えば、オイラー法よりも精度が良い方法といった感じです。
(原理は全く異なるものですが...)
参考
- https://www.kspub.co.jp/book/detail/1572058.html
- http://cms.phys.s.u-tokyo.ac.jp/~naoki/CIPINTRO/CIP/symplectic.html
今回は1次のバイラテラル・シンプレクティック数値積分でシミュレーションを行います。
計算式で表すと、以下のようになります。
\left\{
\begin{array}{ll}
q(t+\frac{\Delta t}{2}) = q(t) + \Delta t \frac{\partial H}{\partial p}_{p=p(t)} \\
p(t+\frac{\Delta t}{2}) = p(t) - \Delta t \frac{\partial H}{\partial q}_{q=q(t+\frac{\Delta t}{2})} \\
p(t+\Delta t) = p(t + \frac{\Delta t}{2}) - \Delta t \frac{\partial H}{\partial q}_{q=q(t+\frac{\Delta t}{2})} \\
q(t+\Delta t) = q(t + \frac{\Delta t}{2}) + \Delta t \frac{\partial H}{\partial p}_{p=p(t+\Delta t)} \\
\end{array}
\right.
q:変位、p:運動量、H:ハミルトニアン
衝突処理についてはGasIntegratorDOPから衝突時のデータを取得し、反映させるようにします。
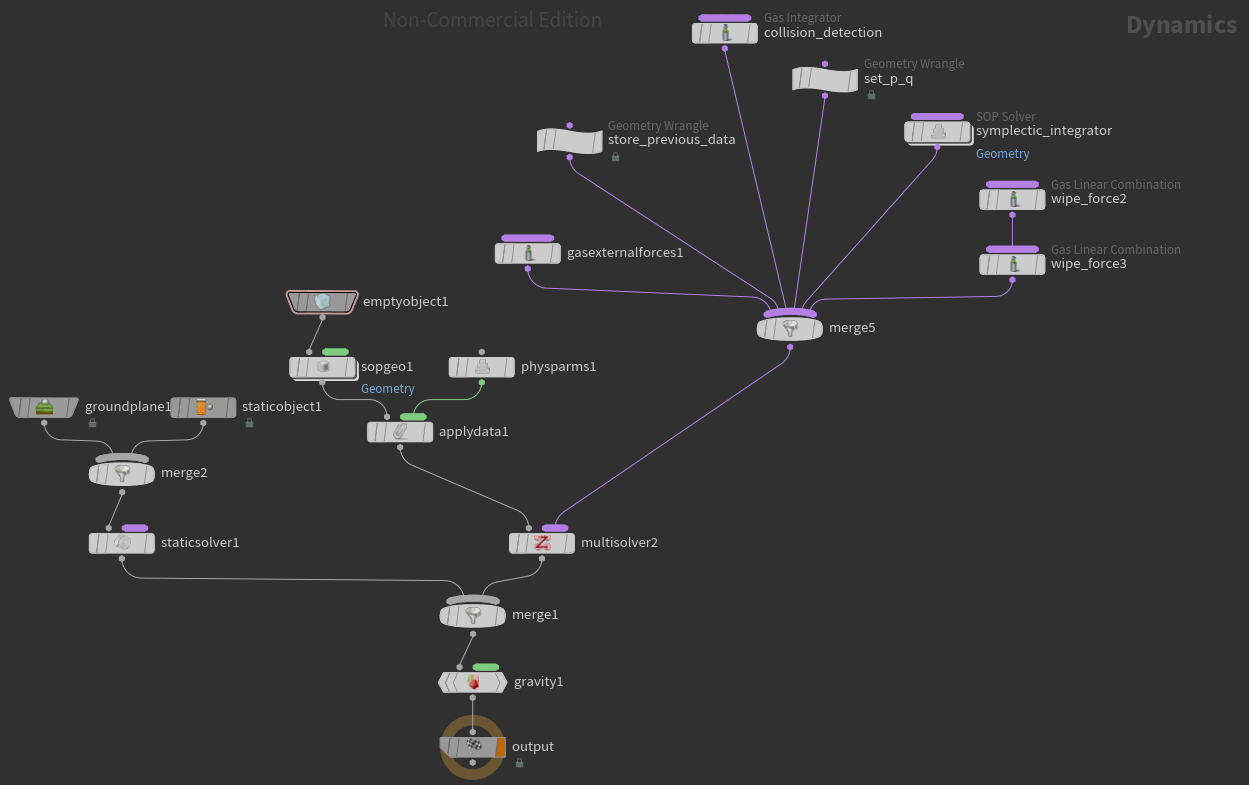
ネットワーク
先ほどのネットワークでのSolver部分だけ変更しています。
Solver部分を拡大すると以下のようにしています。
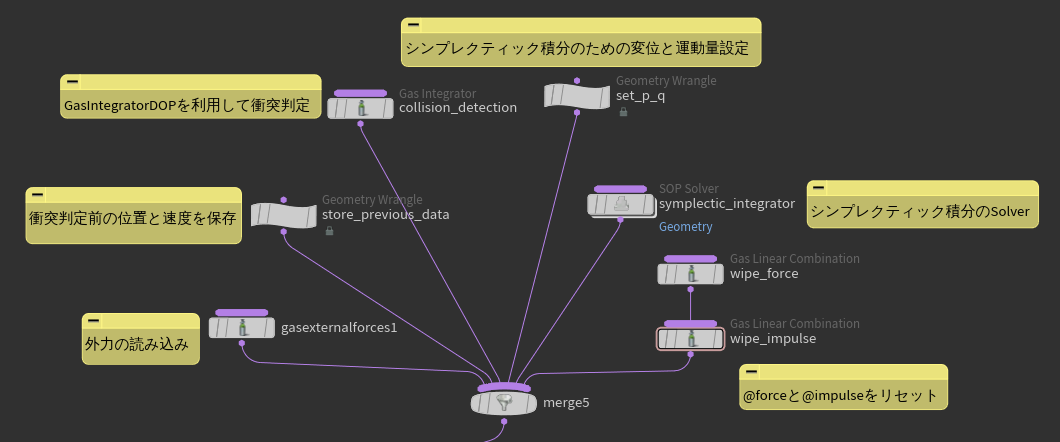
各ノードは画像内のメモに記した通りの計算を行っています。
外力の読み込み
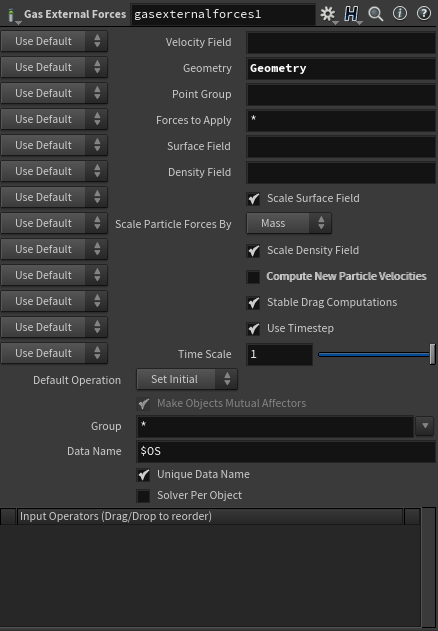
GasExternalForceDOPのパラメータでは先ほどと同様に外力を読み込みますが、今回は速度の更新を自分で行いたいため、ComputeNewParticleVelocitiesのチェックは外しておきます。
衝突判定前の位置と速度を保存
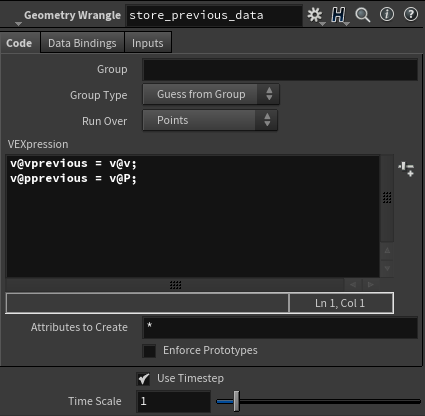
シンプレクティック積分で位置と速度を更新したいので、念のためGasIntegratorDOPの計算の前に位置と速度を別アトリビュートとして保存します。
GeometryWrangleDOPを使っています。
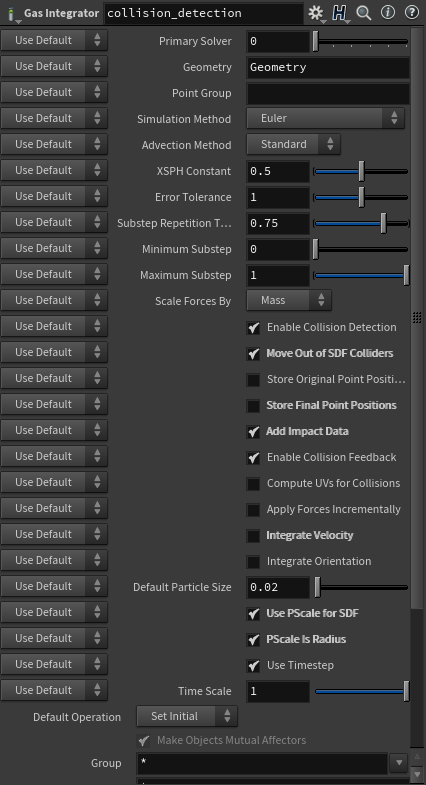
衝突判定
先ほどのGasIntegratorDOPでは位置の更新を行っていましたが、今回は衝突判定だけを行います。
MoveOutofSDFColliderは物体が衝突時に貫入しないためにチェックをつけます。
そして、StoreFinalPointPositionsは必要ないのでチェックを外しています。
また、AddImpactDataのチェックをつけ、衝突時のデータを使えるようにします。
最後に、IntegrateVelocityのチェックを外すことで、位置の更新を行わないようにします。
ここで、AddImpactDataについて追記します。
この項目にチェックをつけると、下図のように衝突時にImpactsというデータがシミュレーションオブジェクトに追加されます。

このImpactsには衝突衝突時の力やその方向、衝突したオブジェクトの情報が含まれています。
GeometrySpreadSheetで見るどんなデータが入っているかがわ分かりますが、このままだと扱いが難しいです。
そこで、SOPSolverDOPを使うことで簡単に扱えるようにします。
変位・運動量の設定
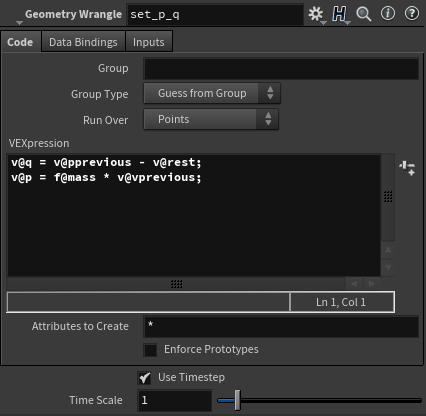
シンプレクティック積分では変位と運動量を使うので、それぞれ計算し、@q,@pのアトリビュートに納めます。
シンプレクティック積分
積分を行う部分はSOPSolverDOPで行っています。
SOPSolverDOPを使うのは先ほど記述したように、Impactsのデータを簡単に扱うためです。
SOPSolverDOPの内部は以下のようにしています。
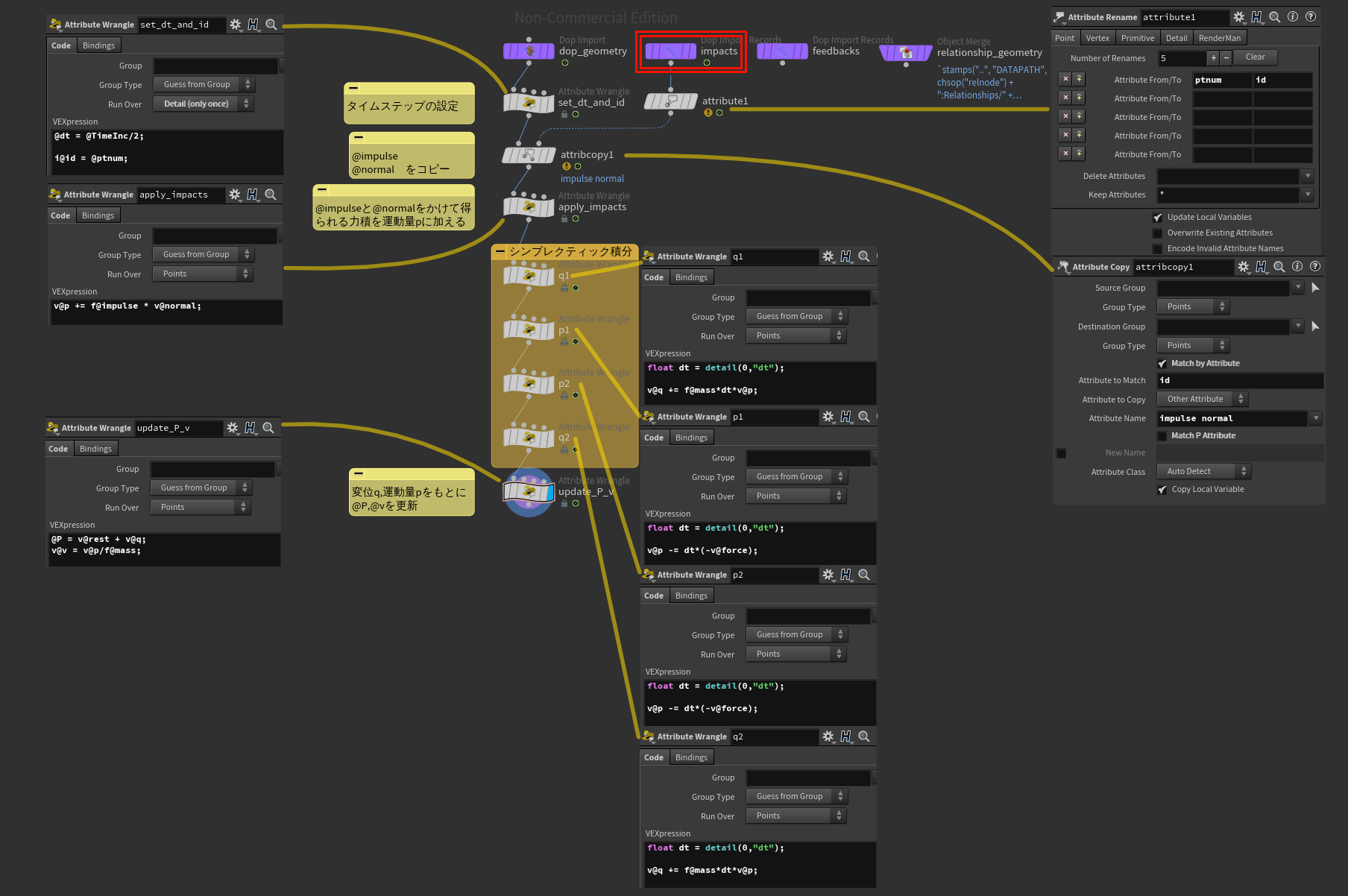
赤枠で囲ったノードから衝突時の情報を得られるので、@idを使ってアトリビュートをコピーしています。
衝突時の力については、@impulseから衝突時の力積の大きさ、@normalから力積が働く方向を得られます。
これらの積をとり、力積のベクトルを求め、運動量@pに加えることで衝突処理を行います。
force,impulseのリセット
GasLinearCombinationDOPをつかうことで、forceとimpulseのアトリビュートをリセットしています。
リセットしないと、外力が毎フレーム加算されてしまいます。
これは、GeometryWrangleDopを使ってコードを書いても問題ないかと思います。


結果
当然ながら、オイラー法とさほど変わりません。
強いて言えば、静止直前まで跳ねているように見えるくらいでしょうか。
正直、映像として使う分にはオイラー法で十分だと思います。
しかし、Houdiniのその柔軟性から、高精度のシミュレーションも実装できることが分かりました。
つまり、Houdiniを力学解析ソフトとして活用することもできるのではないかと思いました。(暴論)
まとめ
シミュレーションオブジェクトとSolverを自作し、簡単なシミュレーションを行うことができました。
また、Solverが自作できるようなったことで、より精度の良いアルゴリズムや最新の研究を実装し、既存のシミュレーションと組み合わせるといったことが簡単にできるようになったと思います。
普段気にすることのないDOP Solverたちの中身を見ると新しい発見もあるかと思います。
是非、Solverの自作を試してみてください。