はじめに
時系列解析ってなるとAR, MA, ARIMAモデルといった伝統的な解析方法から状態空間モデル, Stanによる統計ベイズモデリングなど様々の方法があります。そこにprophetという便利な時系列解析のAPIが出ていたのですね。ですので仮想通貨に対して適用し味見してみました。時系列解析になるとRの方が便利なのでこちらを使っていきます。
pythonでは、@shion1118さんが、Prophetを用いた時系列解析によるビットコイン価格予測を行っていますね。
Prophetとは
CRANのマニュアルのDescriptionを訳しました。
非線形トレンドが年、週、日単位での季節性に加え、休日効果とともにフィットさせる加法モデルに基づく時系列データを予測する手法を実装している。これは強い季節性の効果やヒストリカルデータの複数の季節をもつ時系列データでうまく働く。Prophetは欠損値、トレンドのシフト、そして典型的な外れ値操作に対して頑健性がある(ロバストである)。
状態空間モデルとは
まずは状態空間モデルについて軽くまとめます。状態空間モデルは、「真の状態」と「観測値」を分けて考えるモデルです。式で書くと次のようになります。
\begin{align}
x_t &= F_t x_{t-1} + B_tu_t + \epsilon_t, &\epsilon_t ~ \mathcal{N}(0, H_t)
\\
z_t &= T_t x_t + \eta_t, &\eta_t ~ \mathcal{N}(0, Q_t)\\
\end{align}
ここで、添え字tは時刻を表す。$x_t$ : 状態値, $u_t$ : インプット, $F_t$ : 状態遷移行列, $B_t$:制御行列, $\epsilon_t$:ノイズ(状態攪乱項), $z_t$ : 観測値, $T_t$ : 遷移行列, $\eta_t$ : 観測攪乱項である。
1番目の式が状態を表すシステムモデルです。2番目の式は状態を基にして得られた観測モデルと呼びます。制御理論だとシステムが連続(continuous)なので微分方程式になります。時系列解析では離散(discrete)でありマルコフ過程です。この観測値を平滑化や予測するにはカルマンフィルタを用います。@IshitaTakeshiさんの記事カルマンフィルタってなに?が分かりやすかったです。
状態空間モデルは、観測できない状態を含めることでAR/MA/ARMA/ARIMAなどよりも複雑な時系列モデリングすることができます。ただし、基本的には線形モデルのため実際に株価や為替の予測といったことは難しいです。そこで、非線形モデルならどうか?って思います。prophetは非線形トレンドを持ったモデルを簡単に解析できるという便利なAPIです。こちらの方の式はトレンド、季節、休日要因を足し合わせたcomponentモデルです。
y(t) = g(t) + s(t) + h(t) + \epsilon_t
モデルの詳細は論文に記載されています。
Bitcoinの価格
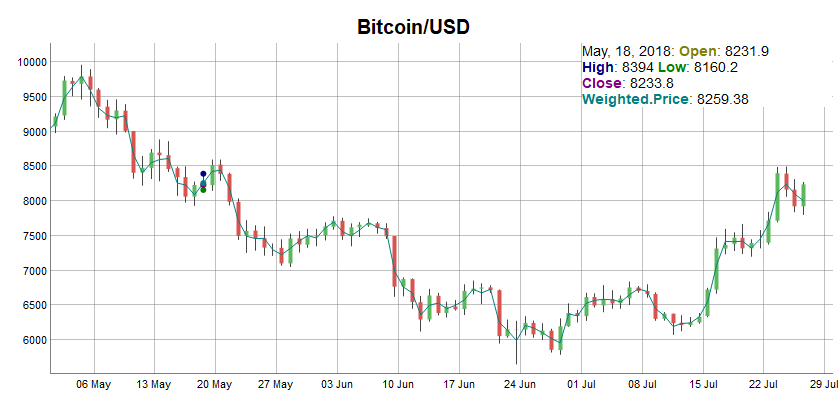
まずは価格がどうなっているか見ましょう。データの元はKRAKENです。データ取得方法は、以前の記事:Pythonで仮想通貨を解析してみた。を参照ください。
library(prophet)
library(dygraphs)
library(dplyr)
df = read.csv('bitcoin.csv') %>% filter(Weighted.Price!=0)
row.names(df) = df$Date
dygraph(df[c(2:5,8)]) %>%
dyCandlestick() %>%
dyRangeSelector(c("2018-05-01", "2018-07-30"))
Rの代入演算子
<-は不等式<と間違えやすいので私は使いません。
0のデータが含まれているので、それら列を除きます。
Prophetにより真の状態と予測値を求める
2014年からの予測
何も考えずにデフォルトで回帰してみます。
df = read.csv('bitcoin.csv') %>% filter(Weighted.Price!=0)
# prophetの形式にする
df = data.frame(ds = df$Date, y = df$Weighted.Price)
n = which(df$ds=="2014-01-07")
m = prophet(df[n:nrow(df),],
growth="linear", n.changepoints = 25, changepoint.range = 0.8,
yearly.seasonality = "auto", weekly.seasonality = "auto", daily.seasonality = "auto",
holidays = NULL, seasonality.mode = "additive", seasonality.prior.scale = 10,
holidays.prior.scale = 10, changepoint.prior.scale = 0.05,
mcmc.samples = 0, interval.width = 0.8, uncertainty.samples = 1000
)
future = make_future_dataframe(m, periods = 1)
forecast = predict(m, future)
dyplot.prophet(m, forecast)
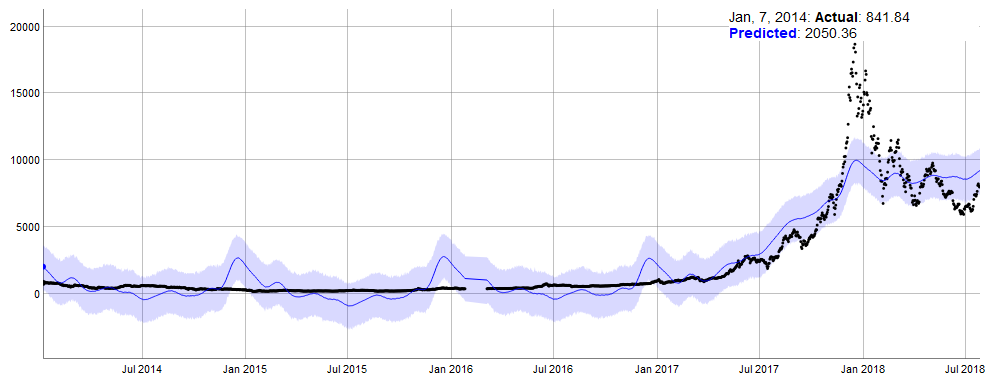
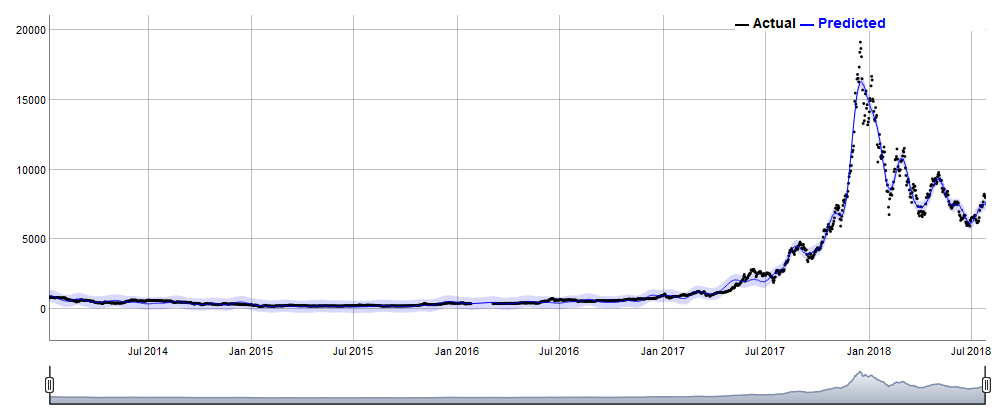
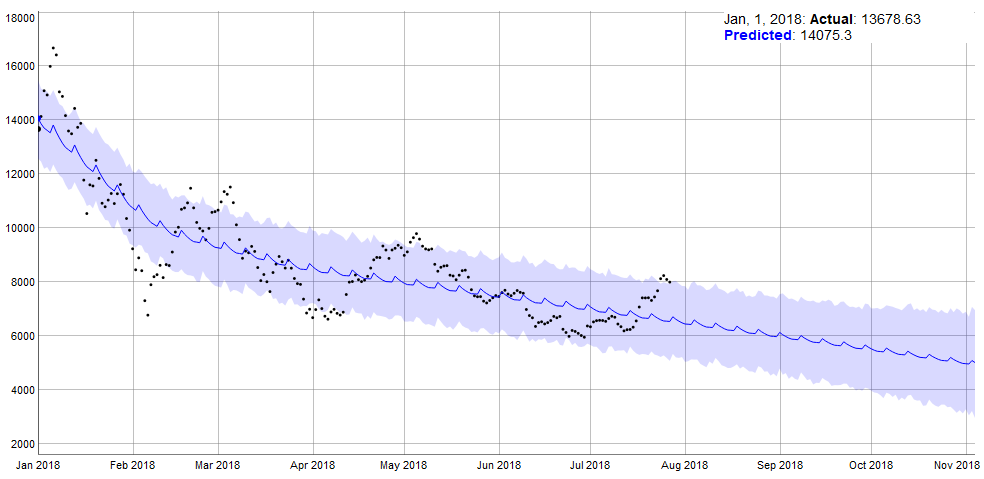
これはひどい結果となりました。予測値(システムの真の状態)と実測値の乖離が激しいです。2018年の1月頃を除けば信頼区間に入っていますが、やはり分散が大きいです。2014年からの日足値を用いたときは予測は困難であることがわかります。これは急騰したときのトレンドを考慮していないためだと思います。
ちなみにこのモデルで無理にでも予測しようとすると、真の状態は8500~9000ドル付近になっており現在の水準で考えると低いので、上昇すると考えられます。
季節性の問題
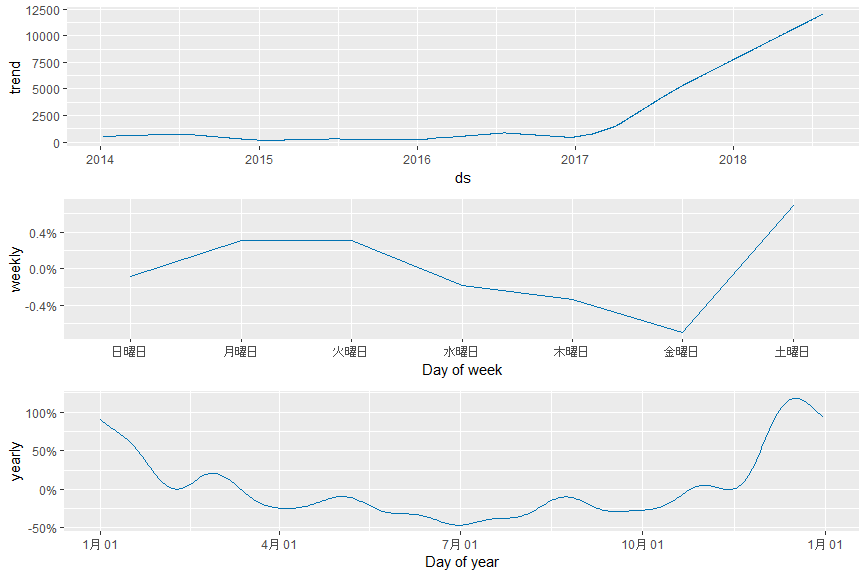
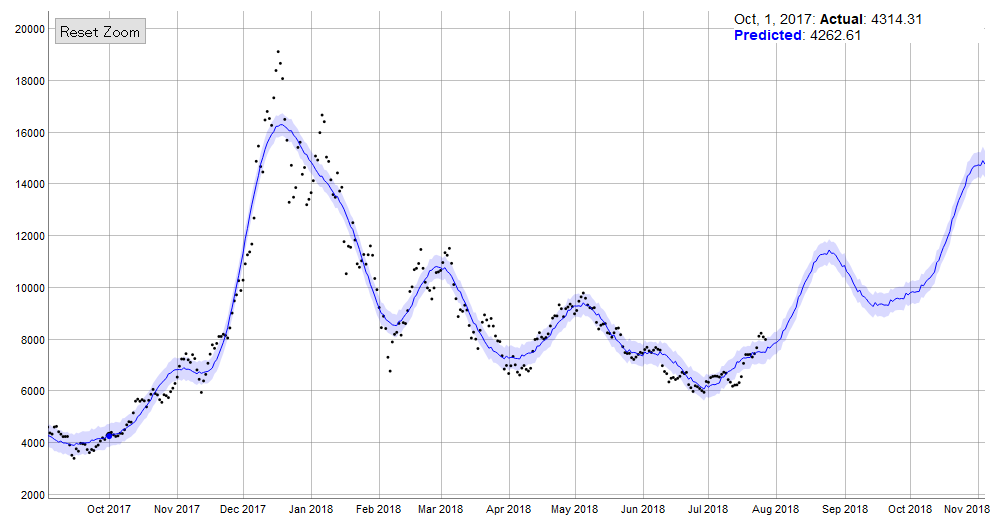
先ほどはseasnality.mode = 'additive'としました。ですが、異常に上昇していることを考慮するとseasnality.mode = 'multiplicative'とした方がよさそうです。変えた結果が下図になります。
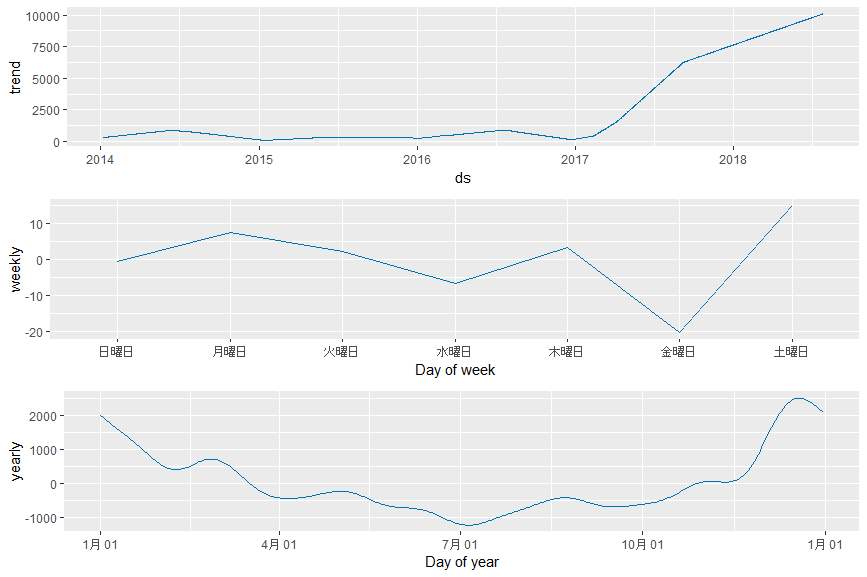
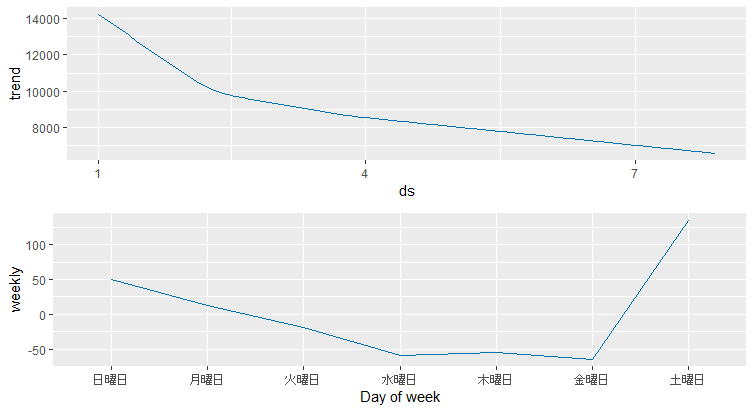
こちらの結果の方が正しそうです。コンポーネントごとの予測は変わりませんが、2017年から上がっているトレンドやweekyでも金曜から土日にかけて上昇するトレンドが見ることができます。なお、このモデルだと2018年末は約15000ドルという予測値になっています。これは2017年末の季節性トレンドを含んでいるためでしょう。
ちなみに図として載せませんが、このトレンドが続くと2020年には50,000ドルの予測、2021年には70,000ドルと予測されてしまいます。
2018年からの予測値
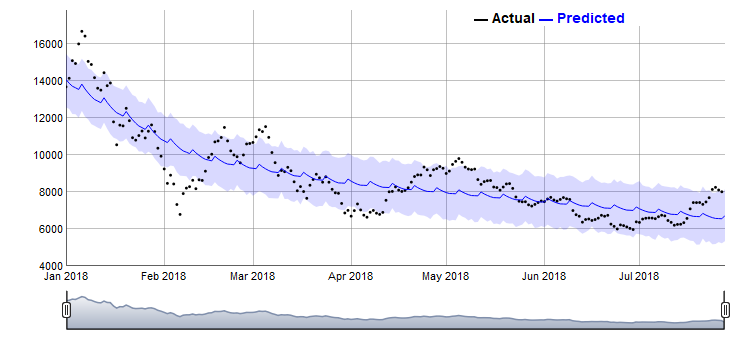
そもそも2014年から考えると現在は仮想通貨の状態が大きく変化しているので、直近の2018年1月からで判断してみたらどうなるでしょうか。
この結果をみると、ダウントレンドにあることがわかります。weeklyを見ると週末は上がっているようです。2018年からのトレンドを見ると、年末には5000ドルと予測されています。
状態空間モデルを考える
参考までに状態空間モデリングでよく使用されるパッケージの1つであるKFAS(Kalman Filter and Smoother for Exponential Family State Space Models)を利用してみます。
library(KFAS)
library(ggplot2)
library(dplyr)
library(xts)
# 状態空間モデルを解く
func.kfs = function(model, inits, n.ahead=5, level=0.95, nsim=1000){
fit = fitSSM(model, inits, method="BFGS") # 準ニュートン法(BFGS)によるパラメータ推定
filter = KFS(fit$model, smoothing = "mean") # カルマンフィルターの適用
# 予測
if(n.ahead==0){
pred = predict(fit$model,interval="confidence"#,level=level, nsim=nsim)
}
else{
pred = predict(fit$model,interval="confidence", n.ahead=n.ahead)
}
return(list(fit=fit, filter=filter, pred=pred))
}
# 可視化
ssplot = function(dat){
y = dat$fit$model$y
d = data.frame(t=c(1:length(y)), y=y)
b = data.frame(dat$pred) %>% rename(y=fit) %>%
mutate(t=time(dat$pred)) # ignore warning
d = bind_rows(d,b)
g = ggplot(d) +
geom_line(aes(x=t, y=y), lwd=1) +
geom_ribbon(aes(x=t, ymin=lwr, ymax=upr), fill="blue", alpha=.2)
print(g)
}
# SSM + arimaモデル
update.fn = function(pars, model) {
model = SSModel(y ~ SSMtrend(2, Q=list(0, 0)) +
SSMarima(ar =artransform(pars[1:2]),
ma=pars[3], Q = exp(pars[4])), H = 0)
model$T["slope", "slope", 1] = pars[5]
return(model)
}
crmodel = function(n.ahead=20){
model = SSModel(y~ SSMtrend(2, Q=list(0, 0)) +
SSMarima(ar=c(0, 0), ma=0, Q=NA), H=0)
fit.model = fitSSM(model, inits=rep(.1, 5),
updatefn = update.fn, method="SANN") # simulated annealing
filter.model = KFS(fit.model$model, smoothing = "mean")
print(paste("Converged: ", fit.model$optim.out$convergence == 0))
print(paste("log likelihood:", round(-fit.model$optim.out$value, 3)))
pred = predict(fit.model$model, n.ahead = n.ahead, interval = "confidence",
type="response", level=.95)
return(list(fit=fit.model, filter=filter.model, pred=pred))
}
# =====================================================
# MAIN
# =====================================================
df = read.csv('./examples/bitcoin.csv', sep=",") %>% filter(Weighted.Price!=0)
n = which(df$Date=="2018-01-07")
y = df[n:nrow(df), "Weighted.Price"]
# 状態空間モデルの作成; NAが求めたいパラメータ(平均、分散など)
mod = SSModel(y~SSMtrend(1, Q=NA), H=NA, distribution="gaussian") # 1次のモデル
mod = SSModel(y~SSMtrend(2, Q=list(NA, NA)), H=NA) # 2次のモデル(勾配も考慮)
inits = numeric(3)
# ssplot(func.kfs(mod, inits, n.ahead = 10))
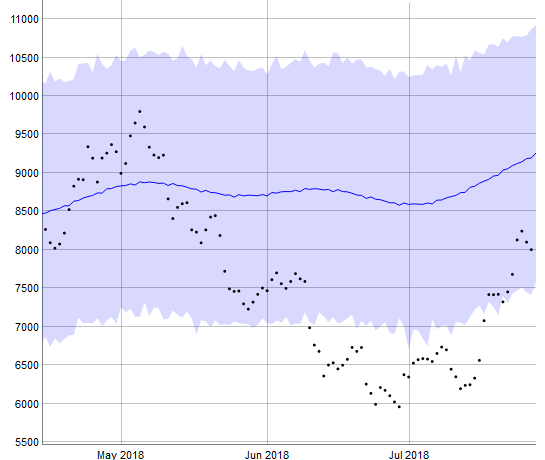
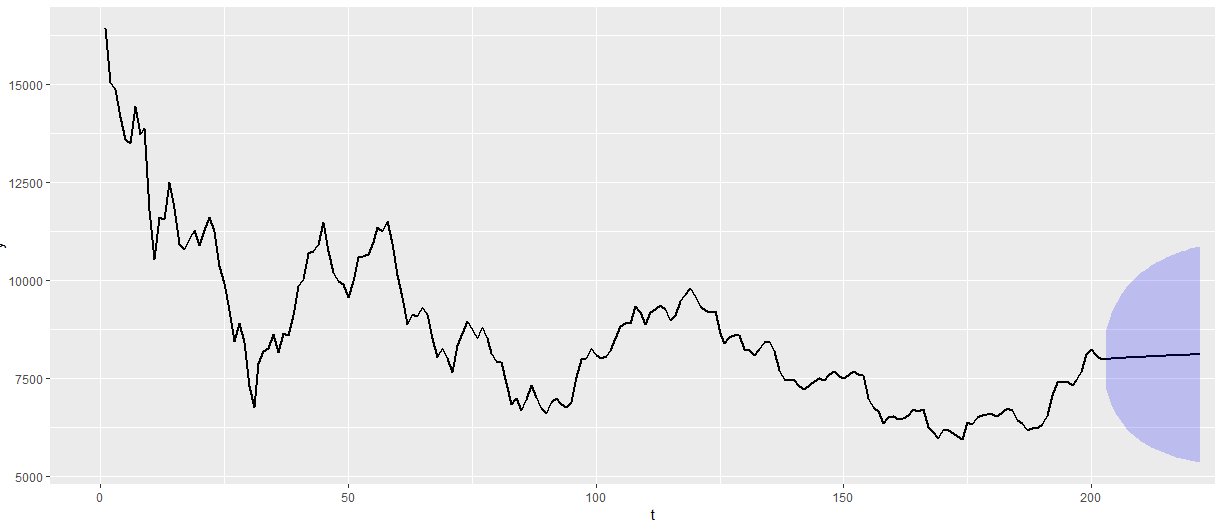
ssplot(crmodel(n.ahead=20))
この結果を見ると予測に関しては全然ダメということがわかります。状態・現象に合わせて正しくモデリングしないと、基本的に平均に落ち着いてしまいます。ここが状態空間モデリングの難しいところです。統計モデリングに使われるStanはKFAS以上に自由度が高く、変なモデルを作ると大抵収束しないので面倒です。その点Prophetは楽に使えてとても便利でした。