連結リストを学ぶ
連結リストを知るには、データ構造を理解しましょう。
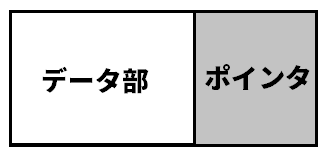
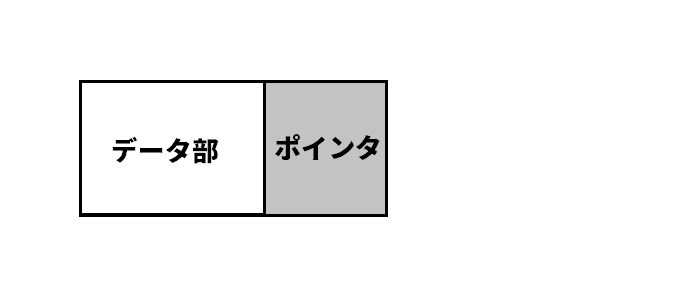
連結リストは、「データ部」と「ポインタ部」で構成されたデータ構造です。
ポインタをたどることでデータを取り出すことができます。
また、ポインタには、次のデータのアドレスが格納されています。
このデータ構造をどのように扱うかによって、さらに複数のデータ構造が作られています。
単方向リンクリスト
単方向リンクリストとは連結リストの一種で、各Nodeが自分自身のデータと隣の要素のリンク(ポインタ)を持っており、先頭から最後尾までがリンクでつながっているのが特徴です。
このようにデータ部とポインタのデータ構造が連結していることが連結リストであり、次のリストを指すポインターが片方しかないものを単方向リンクリストと呼ばれます。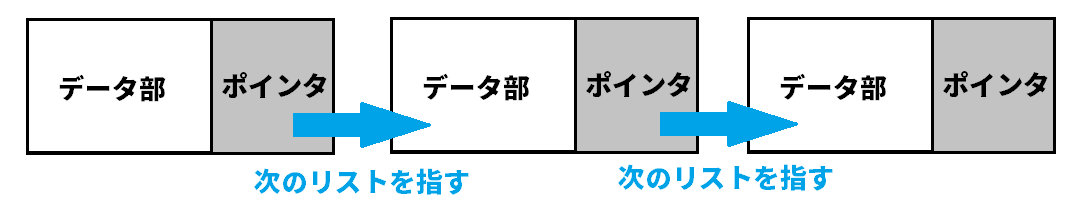
単方向リンクリストは、次のリストへのアドレスを保持していることで成立します。
逆に言えば、単方向リストは自分のデータと次へのアドレスしか関心を持ちません。
単方向リンクリストの特徴
単方向リンクリストの構造は理解できたので、特徴を理解していきましょう。
利点もありますが、制約も多く使われるタイミングは限定されています・・・
必要な分のメモリを確保することができる
よく使われる配列のように、大きめのメモリを確保しておく必要がありません。
常に必要な要素分のメモリだけ確保しておける。
配列の構造が分からない方は、記事の下のほうに配列も説明しているので先に見てください。
連結リストとの話は一旦無視して、こんな構造になっているのかと理解してもらえれば、これから説明することがより分かるかと思います。
挿入や削除が速い
あるNodeの直後に要素を挿入する場合や削除する場合はO(1)で行うことができます。
あるNodeを挿入・削除する場合は、ポインタのアドレスを変更するだけで済みます。
配列はそのようには行きません。(末尾は除く)
配列に対して、挿入・削除する場合は、新たにメモリ領域を1つずつずらす必要があります。
そのため、要素数をnとした場合、平均O(n)です。
O(n)というのは計算量です。
要素が4の場合、O(4)で、計算量のものさしとして使われるので覚えておきましょう!
リストの要素へのアクセスが苦手
特定の要素へアクセスする場合には、先頭から追いかけていくしかありません。
逆参照もできないため、後ろからとも行かず先頭から見ていく方法しかないです。
そのため、あるNodeを取得するのは要素数をnとして平均O(n)です。
そのため結局Nodeを追加する場合、先頭以外の要素へ追加・削除する場合は平均O(n)です。
あくまで追加する場合は平均O(1)です。
単方向リンクリストまとめ
特徴から見ても、リストの先頭への追加・削除とメモリ確保が強味となります。
が、同じ強味をもった双方向リンクリストが使われるのが一般的で単方向リンクリストは用途が限られます。
双方向リンクリスト
単方向リストは次のNodeへの関心しかありませんでした。
双方向リストは次のNodeと前のNodeへ関心を持ちます。
双方向リンクリストの特徴
単方向リンクリストは制限も多く、用途の幅が狭いですが双方向リンクリストはいろいろと応用することができます。
必要な分のメモリを確保することができる
単方向と同様に、必要な分だけのメモリを確保することができます。
挿入や削除が速い
こちらも単方向と同様に、ノードの直後または直前に挿入する場合はO(1)で行えます。
リストの要素へのアクセスが苦手
こちらも単方向と同様に、要素へのアクセスが苦手です。
要素を見つけるには先頭もしくは最後尾から探すしかありません。
そのため平均O(n)です。
単方向より少しメモリが必要
単方向と比べて、前のNodeに関心を持つため少しだけ余分にメモリがひつようになります。
双方向リンクリストのまとめ
要素への検索には時間がかかるものの、挿入や削除に強い点からリスト管理には双方向リンクリストが使われます。
連結リストという言葉は単方向ではなく双方向リンクリストを指すこともあり、C#でもLinkedListという名前で使われています。
よく比較される配列
連結リストを学ぶ上でよく配列と比較されます。
なのでここでは簡単な配列の構造を説明します。
配列は連続したメモリ領域を確保する
配列は固定長のメモリ領域を確保してデータのやりくりをします。
例えば、配列の要素が100個あれば、それ相応の連続したメモリ領域を確保します。
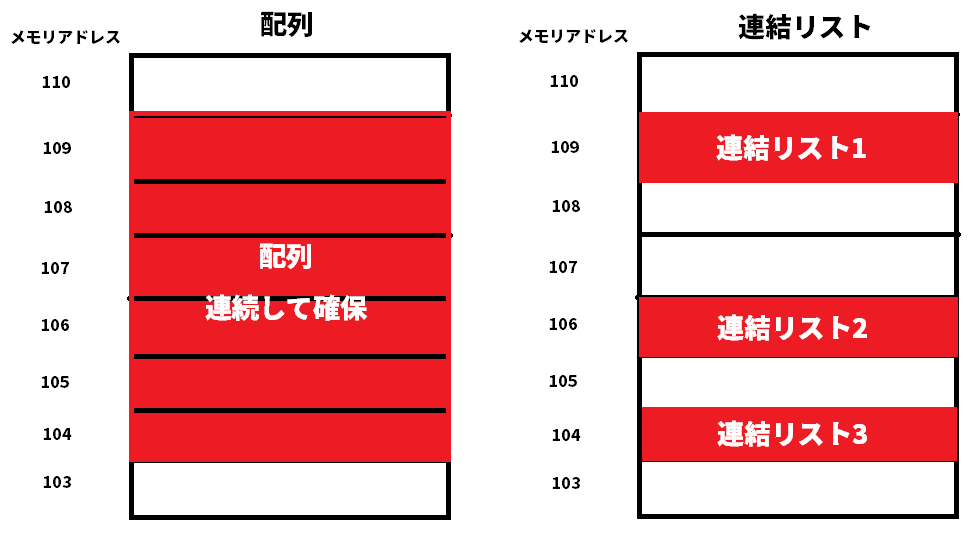
配列は連続したメモリ領域であり、連結リストは次のNodeの場所をポインタで指しているためバラバラでも構いません。
メモリ領域の確保の仕方を図にすると以下のようになります。
本棚などをイメージしてもらえるとより分かりやすいですが、配列はここは〇〇さんの本が並ぶとあらかじめ確保していますが、連結リストは空いてるスペースに格納するので余分なメモリ領域を作る必要がないので都合よく場所を使えます。
各要素へのアクセスが高速
なぜ早いかを理解する前に、配列の特徴を話しますが
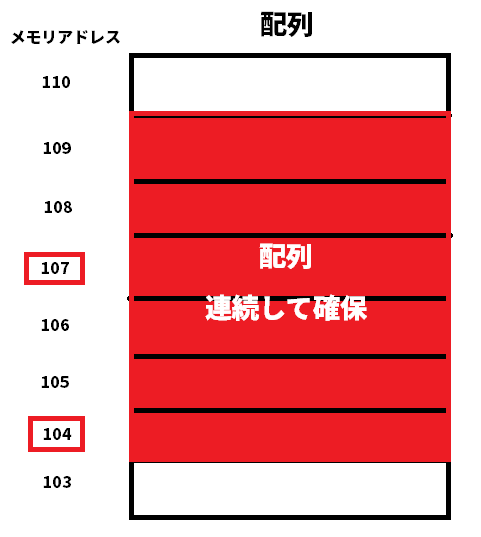
配列は同じ大きさのデータを隙間なく連続的**に並べています。
上記の図では1バイトです。
アクセスが高速な理由はここが重要で、n番目の要素がとりたい場合、先頭のアドレス + (要素の大きさ * n)で求めることができます。
例えば3つめの要素を取得したい場合は、104 + (1 * 3) = 107で3つめの要素が取得できます。
これがインデックス(添え字)となるのですが、このよう計算され取得できます。
一方連結リストは連続したアドレスではない可能性もあるため、配列のような計算はできず、先頭または最後尾からポインタをたどって要素を見つけてくるしかないため探すのが苦手とされます。
要素の追加と削除が苦手
配列は、同じ大きさのデータを隙間なく連続的に並べられています。
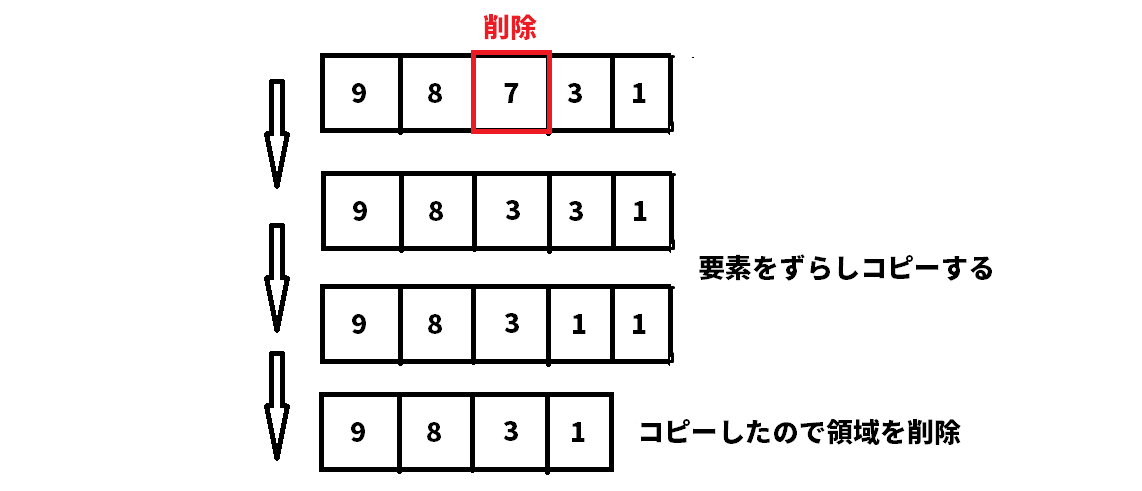
そのため要素が追加・削除される場合に要素をずらす作業が必要となります。
削除した場合の配列処理の図を書きました。
より具体的には違うのかもしれませんが、このような形です。
逆に追加する場合は、一個分の領域を新たに確保して、ずらしコピーを行い、指定した要素の値を書き換えます。
また、追加する場合にスペースが確保できない場合は、配列すべてが収まる場所にコピーする必要があります。
そのため、要素数をnとして平均O(n)かかります。
一方連結リストは単にポインタで場所を指しているだけなため、次もしくは前のNodeの場所を変えてあげるだけで済みます。
まとめ
連結リストの種類(実際は環状リストも存在しますが、単方向環状リストの場合最後のNodeのポインタが先頭を指すループになっているだけなのあで省きました。双方向環状リストも似た感じで先頭の前を示すポインタが最後尾を指している状態)と特徴を説明しました。
また配列の構造も学びました。
配列と連結リストでは得意不得意があります。
個人的には、要素のアクセスが多い場合は配列で、要素を動的に書き換える頻度が多い場合などは連結リストを使ってあげたほうが良いのかなと思います。
配列・連結リストの特徴を理解し今後のプログラミングに活かしていただければと思います。
一旦締めましたが、単方向リンクリストの実際のコードを説明していきたいと思います。
単方向リンクリストのデータ構造のコード
Nodeの構造・連結リストの初期化・追加・削除をやっていきたいと思います。
Nodeの構造
データが入る変数と次のオブジェクトを指すポインターを準備します。
このクラスを利用して連結リストを作っていきます。
class Node(object):
def __init__(self, data: Any, next_node: Node = None):
self.data = data # データ
self.next = next_node # 次のNodeを指す参照変数(ポインタ)
連結リストの初期化
連結リストのクラスを作成して、先頭にNoneを追加しておきます。
この状況はLinkedListをインスタンス化した場合にデータが何も入っていない状態と同じです。
class LinkedList(object):
def __init__(self, head = None) -> None:
self.head = head # インスタンス化した時にNoneをいれておく。
連結リストの要素追加
特徴でお話した通り、追加する場合は最後のNodeまで先頭からたどるため平均O(n)です。
その特徴をコードで表しているのが、whileです。
whileを使って、最後のNodeまで辿っていきnextがNoneなのか見て判断します。
def append(self, data: Any) -> None: # リストへの追加
new_node = Node(data) # 追加する要素をNodeクラスを使ってインスタンス化
if self.head is None: # headがNoneの場合、今回追加する要素は先頭になるため、self.headへ代入
self.head = new_node
return
last_node = self.head
while last_node.next: # whileは.nextがNoneになると抜けるので一番最後まで繰り返す
last_node = last_node.next
last_node.next = new_node # 最後の要素のポインタに今回追加するインスタンスを追加する
連結リストの要素削除
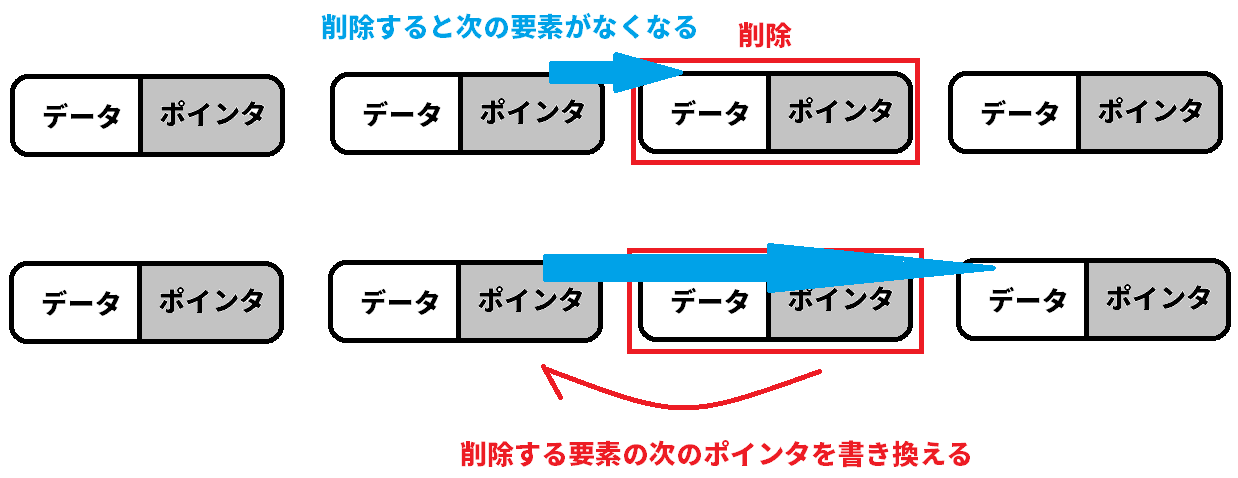
先頭の要素を削除する場合は、先頭の次のオブジェクトを入れてあげればいい。
要素の途中を削除する場合は、先頭から探していき、削除する要素の前のオブジェクトのポインタに削除される要素のポインタを入れてあげればよし。
ただこちらも先頭から探しにいくため平均O(n)となる。
def remove(self, data: Any) -> None:
current_node = self.head
if current_node and current_node.data == data: # 削除したい要素が先頭の場合
self.head = current_node.next # 先頭を次のオブジェクトにする
current_node = None # current_nodeをNodeにする。ガベージコレクションを待ってもいいけど念のため。
return
previous_node = None
# 削除するデータがあるまで、先頭から探す
while current_node and current_node.data != data:
previous_node = current_node
current_node = current_node.next
if current_node is None: # current_nodeがNoneになった場合、削除する値はリストにないのでrerutn
return
# 削除する要素があったら
previous_node.next = current_node.next # currentは削除されるため、その前のオブジェクトにcurrentのポインタを代入
current_node = None # ガベージコレクションを待ってもいいけど念のため。
連結リストまとめ
このようにデータ構造自体はとてもシンプルでわかりやすいと思います。
双方向リンクリストもNodeオブジェクトにprevという参照変数を作ってあげれば実現できます。
正直、自分は日頃から使うような仕事はしていません。
ただし、このような表現の幅を広げることで、利用しているツールのデータ構造を理解するのに役に立ちます。
また、構造を考える際に1つの案として表現の幅を広げられます。
書けるようになるのがゴールというより、こういった構造を理解して必要なときに案としてもってこれるかが重要だと思っています。
まだまだたくさんの代表的なデータ構造はありますので、勉強していきたいと思います。
ありがとうございました!