かんたん可視判定(2D/3D)

今日は単純な可視判定について考えます。
ある点Pが、特定のキャラクター(カメラ)の可視範囲内にあるのかどうなのかを判定する方法です。

相手が「点」なら簡単なんです。点ならね。
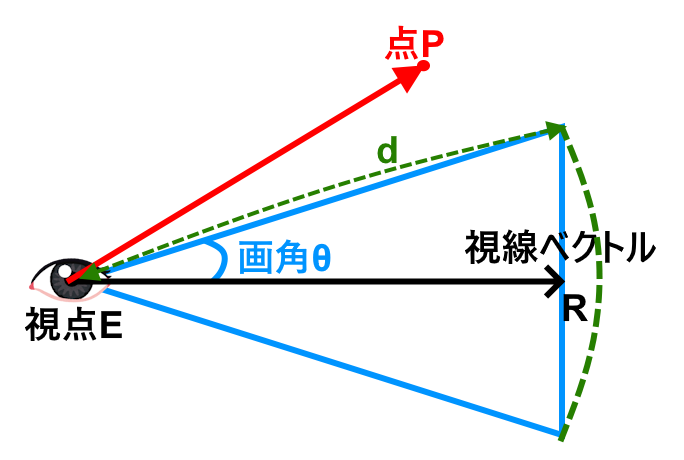
画角がθだとして、視点の座標をE、見える範囲をdだとすると

こんな感じの図になるとします。という事はまず視点Eから点Pまでの距離$$|\vec{EP}|$$がd以下であることが必要ですね。

\|\vec{EP}\|\le d

しかしそれだけでは、画角からはみ出た場合に判定できませんので、画角からはみ出ているかどうかを判定します。
これには、内積の性質$$\vec{A}\cdot \vec{B}=|\vec{A}||\vec{B}|cosθ$$を利用します。
この式を変形すると

cosθ=\frac{\vec{A}\cdot \vec{B}}{\|\vec{A}\|\|\vec{B}\|}

これで得られたcosθは角度が広がれば広がるほど小さくなります。90°以上に広がるとマイナスになります。

という事は、視線ベクトルとEPベクトルの内積結果を視線ベクトルの大きさおよびEPベクトルで割ったものをcosφとすると
cosφ≦cosθ (θは画角)
になればよい。つまり

\frac{\vec{EP}\cdot\vec{R}}{\|\vec{EP}\|\|\vec{R}\|} \le cosθ

になる。
先述の距離の計算と、このcosの計算が成り立てば、その特定の点は視線方向を中心とした画角θの範囲内に入り、半径dの範囲内に入るという事になります。

まとめると

\|\vec{EP}\|\le d

\frac{\vec{EP}\cdot\vec{R}}{\|\vec{EP}\|\|\vec{R}\|} \le cosθ

の式双方が成り立っていれば、ある点は可視オブジェクトであると言えます。

しかし、これが点でなく大きさを持った円(もしくは球)となるとなかなかヤヤコシイ

判定したいのが点ではなく円の場合(2D)

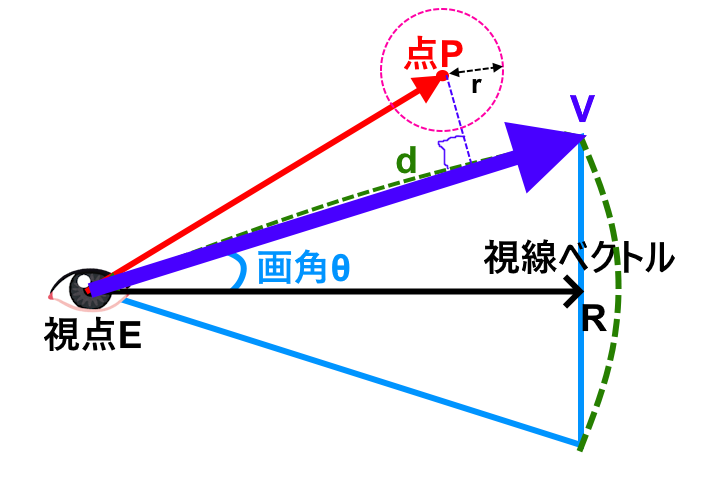
3Dになるとだいぶややこしいのですが、2Dの場合はまだ比較的簡単です。まず視野角が決まっている場合視野角の恥を表すベクトルは２つになりますが、そのうち近い方をVとします。

で、このとき点Pから垂線をVにおろします。この垂線が円の半径r以内ならVに触れる事になります。
通常、垂線を作るには外積を使うか、射影ベクトルを使いますが、今回は射影ベクトルを使いましょう。

射影ベクトルとは、Vベクトルの方向を向きつつ、点Pから垂線を下したところまでの長さを表します。これをたとえば

\vec{W}=\frac{\vec{EP}\cdot \vec{V}}{\|\vec{V}\|}

とすると、垂線ベクトルはEPベクトルからこのWを引けばいいため垂線ベクトルをTとすると

\vec{T}=\vec{EP}-\vec{W}

になります。このベクトルTの長さを求めて、半径ｒと比較すればすべてうまくいくように思えますが、それはあくまでも垂線を下したのがVの長さの範囲内に入っている場合です。Ｖの長さの範囲外の場合もあるためＷの計算を書き換えます。

\vec{W}=clamp(\frac{\vec{EP}\cdot \vec{V}}{\|\vec{V}^2\|},0,1)\|\vec{V}\|

式のようにさらにＶの大きさで割る事でＶベクトルの範囲内にあるなら、値が0～1になります。Ｖの範囲を超えると1以上もしくは0未満になります。これをclamp関数(特定の値を超えたら指定の値にしてしまう)で範囲を限定したうえで、さらにVの大きさをかけることで、Ｗの範囲がＶの長さの範囲内にとどまります。

あとはこれでできたＷから差分ベクトルＴを求めれば、ＷがＶの範囲内なら垂線に、ＷがＶの範囲を超えたなら単純な単店との距離になります。つまりここまでやった

\vec{T}=\vec{EP}-\vec{W}

の長さと半径を比較します

\|\vec{T}\| \le r

が、2Dにおける視野内に円が入ってるかどうかの判定になります。

というよりこうなると扇形と円の当たり判定ですね。

3Dの場合はコーン(円錐)と球の当たり判定になり、急に難易度が上がるので、それは次の機会にしましょう。

それではさようなら