Nishika「中古マンション価格予測 2023冬の部」で4位だったのでまとめ

1. 概要

今回コンペに参加して4位を収めることができたので、まとめてみました。
本コンペティションのテーマは国内の中古マンションの価格推定です。

目次

1. 概要
2. 最低限の前処理とベースラインモデルの作成(LightGBM)
3. 前処理
   3.1 精度が上がらなかった例
   3.2 精度が上がった前処理
4. モデル作成
   4.1 グリッドサーチ、ランダムサーチ検討
   4.2 手動でハイパーパラメータ調節
   4.3 Optunaによるハイパーパラメータの最適化
   4.4 再度手動でパラメータ調節
5. まとめ

1. 概要

評価指標は「MAE」

MAEの特徴

実際のデータと予測値の差の絶対値の平均
・外れ値の影響を少なくした処理をしたデータに有効
・xgboostを使用できない
・代わりの関数として、「Fair関数」や「Psuedo-Huber関数」を用いる。

2. 最低限の前処理とベースラインモデルの作成(LightGBM)

最低限の前処理(なんだかんだ、ここが一番大変、、、)

• trainデータは都道府県別で47個に分かれているので、for文を用いて読み込んで1つのDFに結合
• trainデータ,testデータの結合(前処理で二度手間を防げるので極力結合しておいた方が良い。)
• trainデータ,testデータ共に、'地域','土地の形状','間口','延床面積（㎡）','前面道路：方位','前面道路：種類','前面道路：幅員（ｍ）'が全て欠損値
  →削除しても問題なし(実際に有無で対照実験したがpublicスコア変わらず)
• '建築年'は和暦を西暦に変換する。def,for文を用いて、変換する。ここはコンペのテンプレートコードから参考にしても良いかと。
• 文字型(object)のものを数値型に変換する。主に'取引時点',最寄駅：距離（分）,面積（㎡）,建築年
• カテゴリ変数の変換
  最寄駅：名称,都道府県名,市区町村名,地区名,間取り,用途,都市計画,取引の事情等,建物の構造は要素数も多かったのでlabel encoding。各文字列を本質的に意味のない数値型として変換した。
  '今後の利用目的','改装'は要素数が少なかったので、one-hot-encodingした。

ベースラインモデルの作成(LightGBM)

• train_test_split関数を用いてhold-out法で分割する
• シンプルなパラメータの設定だけするLigthGBM

# パラメータの設定
parms = {
    'task': 'train', #トレーニング用
    'boosting': 'gbdt', #勾配ブースティング決定木
    'objective': 'regression_l1', #目的：MAE
    'metric': 'mae', #評価指標：正答率
    'num_iterations': 1000, #1000回学習
    'verbose': -1 #学習情報を非表示
}

ベースラインモデルの精度は MAE 0.0871325

このときのPublicスコアは0.095668。67位/278位。
この精度を元に前処理やパラメータチューニングを行う。

3. 前処理

3.1 精度が上がらなかった例

• 面積と容積率を組み合わせて新たな特徴量を作る。
  容積率（％）：建物の延べ面積（延床面積）の敷地面積に対する割合。これが大きいと高層マンションの可能性がたかい。
  容積率×面積が大きいとそれほど、その部屋の家賃相場は上がると考えられる。
  建ぺい率：建物が占める土地面積/庭なども含めた敷地面積 ×100
  →精度下がった。
• 特徴量生成
  '最寄駅：距離（分）', '面積（㎡）', '建ぺい率（％）', '容積率（％）'をそれぞれ、'市区町村名'でグループ化して、平均や最大値、最小値を求めた特徴量を追加したが、、
  →精度下がった。(相関の強い特徴量が加わっただけなので、LightGBMに対しては適切な処理ではなかった可能性)

3.2 精度が上がった前処理

• logを取る
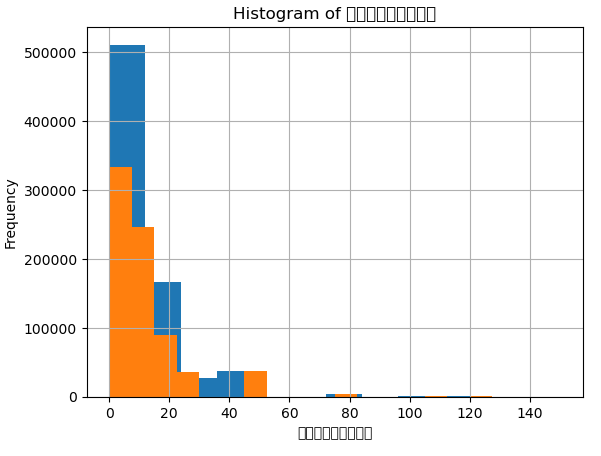
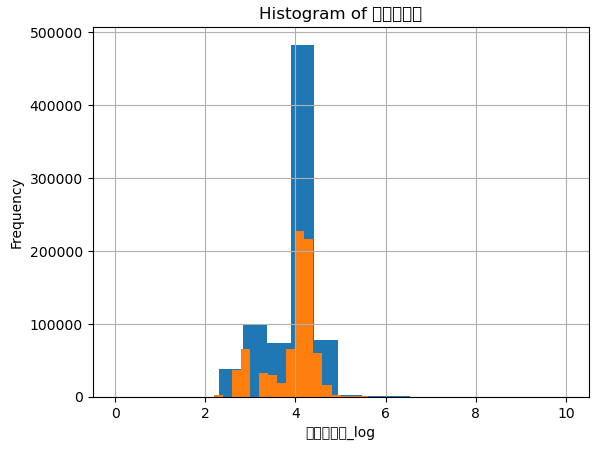
  "面積（㎡）","最寄駅：距離（分）"をそれぞれヒストグラムを取った時に、左に偏った分布をしていた。
  そのため、常用対数logを取ることで、正規分布に近づけた。

左のグラフはそのままの数値の"最寄駅：距離（分）"。右の図はlogを取った後のヒストグラム。
logを取ったものを特徴量として追加して、"面積（㎡）","最寄駅：距離（分）"を削除した。

4. モデル作成

4.1 グリッドサーチ、ランダムサーチ検討

グリッドサーチと、ランダムサーチは設定範囲をもう少し考慮すればよかったが、処理に時間がかかりすぎた。

4.2 手動でハイパーパラメータ調節

• ハイパーパラメータを適当に設定して、LightGBMを回してみる。

params = {
    'objective': 'regression', #目的関数を指定します。回帰問題の場合は、regressionを指定
    'metric': 'mae', # 評価指標を指定します。回帰問題の場合は、maeを指定
    'num_leaves': 42, #決定木の葉の数を指定します。この値を大きくすると、より複雑なモデルなる
    'max_depth': 7, #定木の深さの最大値を指定します。この値を大きくすると、より複雑なモデルになる
    "feature_fraction": 0.8, #各木で使用する特徴量の割合を指定します。過剰適合を抑制するために使用される
#バッチングサンプリング：学習データをバッチと呼ばれる小さなサイズのグループに分割し、その中からランダムにサンプリングする方法のこと
    'subsample_freq': 1, #バッチサンプリングの頻度を指定します。値が大きいほど、より多くのデータを使用される
    "bagging_fraction": 0.95, #バッグサンプリングで使用するサンプルの割合を指定します。過剰適合を抑制するために使用される
    'min_data_in_leaf': 2, #1つの葉に最低何個のデータポイントが必要かを指定します。
                           #この値が小さいほど、過剰適合のリスクが高まりますが、大きい場合はモデルが学習するのに時間がかかる可能性がある。
    'learning_rate': 0.1, #勾配ブースティングにおけるステップサイズを指定します。
                          #この値が小さいほど、モデルの収束が遅くなりますが、より正確な予測が可能になる
    "boosting": "gbdt", #使用するブースティングアルゴリズムを指定します。"gbdt"はGradient Boosting Decision Treeの略
    "lambda_l1": 0.1, #L1正則化の強さを指定します。L1正則化は、特徴量選択に役立つ
    "lambda_l2": 10, #L2正則化の強さを指定します。L2正則化は、過剰適合を抑制するために使用される
    "verbosity": -1, #出力レベルを設定します。-1は、ログを表示しないことを意味する。
    "random_state": 42, #ランダムシードを指定します。同じランダムシードを使用することで、実行ごとに同じ結果を得ることができる。
    "num_boost_round": 50000, #ブースティングの反復回数を指定します。
                              #この値が大きいほど、より多くの反復が行われますが、過剰適合のリスクが高まる可能性がある。
    "early_stopping_rounds": 100 #早期停止のための回数を指定します。モデルの性能が改善しなくなった場合、指定された回数後に学習が停止する。
}

→ベースラインモデル(0.0871325)に比べると、精度は上がった。

ベースラインモデル作成時の前処理のままで、手動でハイパーパラメータを調節する。
↓

params = {
    'objective': 'mae', #目的関数を指定します。回帰問題の場合は、regressionを指定
    'metric': 'mae', # 評価指標を指定します。回帰問題の場合は、maeを指定
    'num_leaves': 10, #決定木の葉の数を指定します。この値を大きくすると、より複雑なモデルなる
    'max_depth': 7, #定木の深さの最大値を指定します。この値を大きくすると、より複雑なモデルになる
    "feature_fraction": 0.5, #各木で使用する特徴量の割合を指定します。過剰適合を抑制するために使用される
#バッチングサンプリング：学習データをバッチと呼ばれる小さなサイズのグループに分割し、その中からランダムにサンプリングする方法のこと
    'subsample_freq': 1, #バッチサンプリングの頻度を指定します。値が大きいほど、より多くのデータを使用される
    "bagging_fraction": 0.95, #バッグサンプリングで使用するサンプルの割合を指定します。過剰適合を抑制するために使用される
    'min_data_in_leaf': 100, #1つの葉に最低何個のデータポイントが必要かを指定します。
                           #この値が小さいほど、過剰適合のリスクが高まりますが、大きい場合はモデルが学習するのに時間がかかる可能性がある。
    'learning_rate': 0.1, #勾配ブースティングにおけるステップサイズを指定します。
                          #この値が小さいほど、モデルの収束が遅くなりますが、より正確な予測が可能になる
    "boosting": "gbdt", #使用するブースティングアルゴリズムを指定します。"gbdt"はGradient Boosting Decision Treeの略
    "lambda_l1": 0.1, #L1正則化の強さを指定します。L1正則化は、特徴量選択に役立つ
    "lambda_l2": 10, #L2正則化の強さを指定します。L2正則化は、過剰適合を抑制するために使用される
    "verbosity": -1, #出力レベルを設定します。-1は、ログを表示しないことを意味する。
    "random_state": 42, #ランダムシードを指定します。同じランダムシードを使用することで、実行ごとに同じ結果を得ることができる。
    "num_boost_round": 5000, #ブースティングの反復回数を指定します。
                              #この値が大きいほど、より多くの反復が行われますが、過剰適合のリスクが高まる可能性がある。
    "early_stopping_rounds": 100 #早期停止のための回数を指定します。モデルの性能が改善しなくなった場合、指定された回数後に学習が停止する。
}

手動でハイパーパラメータ調節するときの考え方

今回、validデータでの精度と、publicデータでの精度に差があったので、過学習気味なのかなと考えた。そこで、モデルが複雑になり精度は上がるが、過学習の原因になるハイパーパラメータを調節した。具体的には'num_leaves',"feature_fraction",'min_data_in_leaf',"num_boost_round"を調節した。

ハイパーパラメータを最適化する

グリッドサーチと、ランダムサーチは設定範囲をもう少し考慮すればよかったが、処理に時間がかかりすぎたので、optunaでチューニングすることにした。

# ハイパーパラメータの最適化
def objective(trial):
    params = {
        'num_leaves': trial.suggest_int('num_leaves', 2, 100),
        'max_depth': trial.suggest_int('max_depth', 2, 10),
        'feature_pre_filter': False,  # feature_pre_filterをfalseに設定する
        'feature_fraction': trial.suggest_uniform('feature_fraction', 0.1, 1),
        'subsample_freq': trial.suggest_int('subsample_freq', 1, 10),
        'bagging_fraction': trial.suggest_uniform('bagging_fraction', 0.1, 1),
        'min_data_in_leaf': trial.suggest_int('min_data_in_leaf', 10, 150),
        'learning_rate': 0.1,
        'boosting': 'gbdt',
        'lambda_l1': trial.suggest_loguniform('lambda_l1', 1e-8, 10.0),
        'lambda_l2': trial.suggest_loguniform('lambda_l2', 1e-8, 10.0),
        'verbosity': -1,
        'random_state': 42,
        'num_boost_round': 5000,
        'early_stopping_rounds': 100,
        'objective': 'l1',
        'metric': 'mae'
    }
    
    # LightGBMのモデルを作成
    model = lgb.train(params, train_data, valid_sets=[train_data, valid_data], verbose_eval=False)
    
    # バリデーションデータに対する予測値を計算
    y_pred = model.predict(va_x, num_iteration=model.best_iteration)
    
    # 平均絶対誤差（MAE）を計算して返す
    return mean_absolute_error(va_y, y_pred)

study = optuna.create_study(direction='minimize')
study.optimize(objective, n_trials=100,timeout=10800) #timeoutの時間を3時間に設定。

# 最適なハイパーパラメータを出力
print(study.best_params)

上記のoptunaによりハイパーパラメータ出力して、ベースラインモデルのlightGBMのパラメータに代入して、予測する。

この時、validデータの精度はMAE0.0657
Publicデータは0.0733。

4.4 再度手動でパラメータ調節

• 'objective'を'mae'から'l1'にしたことで若干精度向上。

過学習気味かなと思い、色々調節したがさすがにoptunaで調整後だったので思うようには上がらず、、
しかし、MAEは平均絶対誤差を最小にするようにする学習オプションで、l1はL1正則化項を含んだ平均絶対誤差を最小にする学習オプションです。また、l1は、予測値と実際の値の差の絶対値を最小化するだけでなく、重みの絶対値の和を小さくすることを目的としています。これにより、過剰適合を防止できます。

5. まとめ

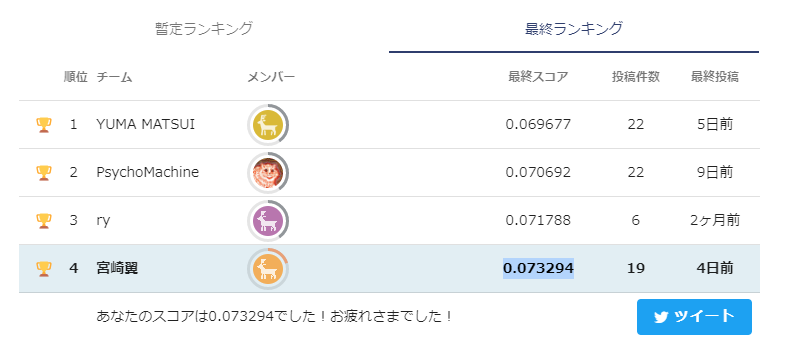
コンペの結果としては、精度MAE 0.073294(4位/287位)でした!!
最終的には、面積と、最寄駅からの分数にlogを取った特徴量を追加してlightGBMをしただけなので、正直これだけでも、意外に精度上がるんだなっと思いました。
前処理自体は手間のかかるものが多くありましたが、飛躍したアイディアというよりは、一つ一つ丁寧にデータ型を変える作業でした。

ソースコードはありませんが、ネットに参考になる記事は山ほどあるので一つ一つ読んで自分で出来そうな範囲で取り入れていくので十分勉強にもなると思います。
また、基本困ったらchatGPTで調べて進みました。一問一答でヒントになる回答が出るので、エラーの対処にも活用できるかと思います。

自分で考えて、前処理やパラメータを調節して精度、順位が上がるとテンション上がるので、地道ですが頑張ってください!!