統計検定1級対策 各分布の特徴の覚え方1 分布一覧編

『統計検定1級対応 統計学』で紹介されている以下の分布について、
期待値・分散・その他特徴の覚え方などをまとめました。
数学的に厳密でないところは目をつぶっていただければと思います。

• 基本的な離散分布（8個）
  離散一様分布、ベルヌーイ分布、二項分布、ポアソン分布、超幾何分布、幾何分布、負の二項分布、多項分布

• 基本的な連続分布（10個）
  連続一様分布、正規分布、指数分布、ガンマ分布、ベータ分布、コーシー分布、対数正規分布、ワイブル分布、ロジスティック分布、多変量正規分布

• 標本集計・検定用分布（3個）
  $\chi^2$分布、$t$分布、$F$分布

以下の表記を用います；

• pdf: 確率密度関数
• ${\rm i.i.d}$: 互いに独立に同一分布に従う
• $E[X]$: $X$の期待値
• $V[X]$: $X$の分散

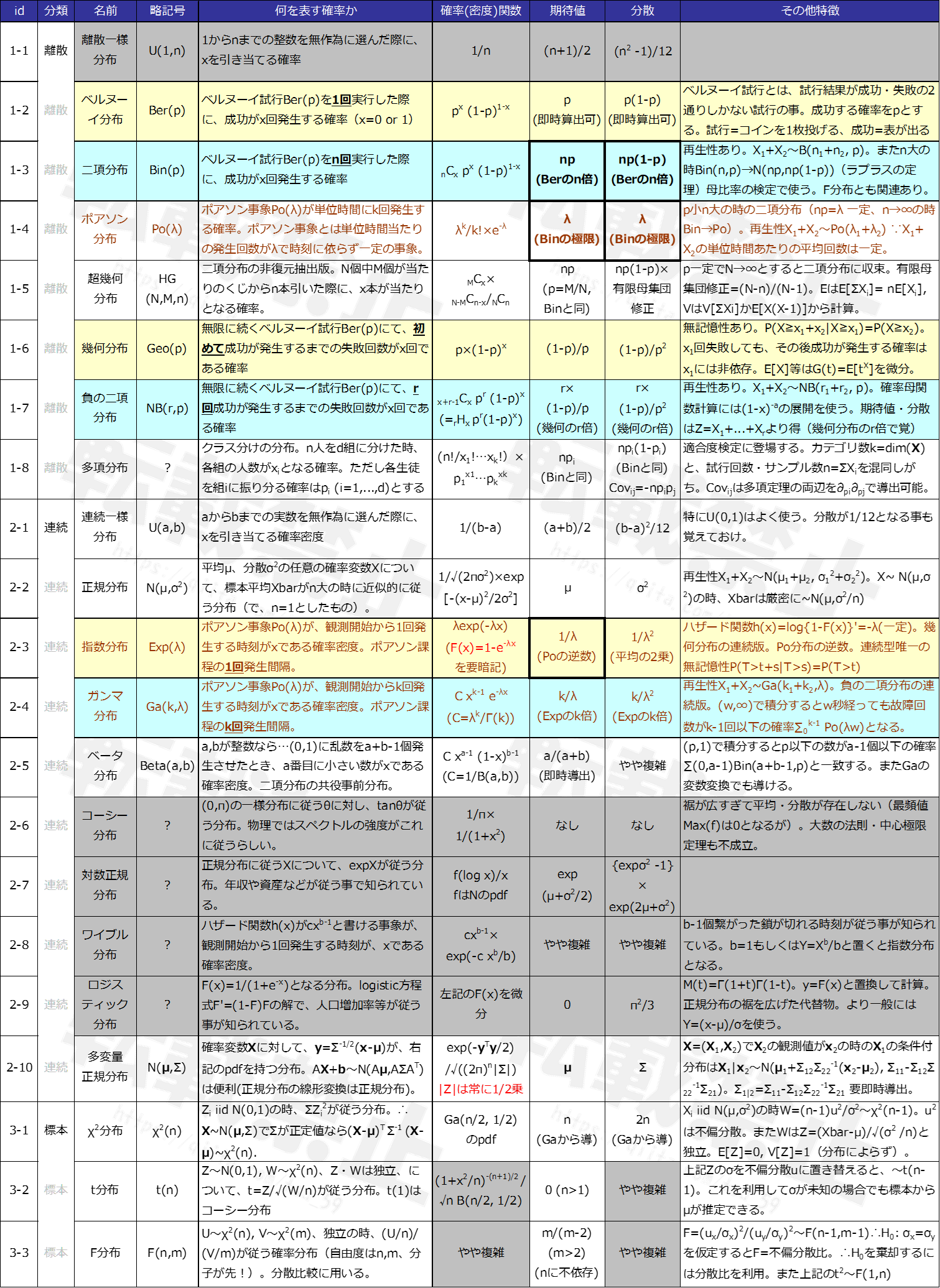
分布一覧・まとめ

各分布のpdf、期待値、分散等を一覧にしました。
特に、期待値・分散については覚えやすくするための工夫をまとめています。
まずは「何を表す確率か」と期待値・分散を覚えて、
残りは定期的に読み返したり書き写したりして頭に入れていければと思います。

書式の凡例

Notation
標本平均をbarで表しています；Xbar$=\bar{X}=\frac{1}{n}\Sigma_{i=1}^n X_i$
不変分散をu²で表しています；u²$=\frac{1}{n-1} \Sigma_{i=1}^n (X_i-\bar{X})^2$
フォントの都合でnと$\pi$が識別困難です、注視お願いしますm(__)m

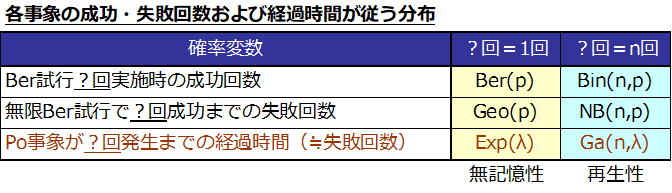
分布同士の関係

薄黄と水色の分布6つを整理するとこうなります。
分布一覧の「何を表す確率か」から自然と導ける関係性です。

また分布一覧にも記載がありますが、下記の関係も試験ではよく使います。
覚え方は…別途まとめようか検討中です。

• $Bin(n,p) \rightarrow Po(\lambda) \hspace{5pt} (\lambda=np一定で n \rightarrow \infty) $
• $Bin(n,p) \rightarrow N(np, np(1-p)) \hspace{5pt} (n \rightarrow \infty) $
• $HG(N,M,n) \rightarrow Bin(n,p) \hspace{5pt} (p=M/N一定で N \rightarrow \infty) $
• $Exp(\lambda)$のpdfは$Po(\lambda)$の確率関数から導ける

「分布同士の関係をまとめる」と言うともっと網羅度の高い、複雑な図を作る方もいますが、
個人的には最低限これぐらいの内容が覚えられていれば、試験対策としては十分かなと思います。
複雑な図は、作る分には良いのですが見返しても覚えられないので。。

無記憶性・再生性

無記憶性・再生性を持つ分布の覚え方

• “薄黄”は無記憶性を、“水色”は再生性を持つ
• “水色”の他、$N$と$Po$も再生性を持つ

です。
なお、“薄黄”の3つの分布のうち、
$Ber$は試行に繰り返し要素が無いため通常は無記憶性を持つとは言いませんが、
覚えやすくするためにその辺は無視でお願いします。

各分布が無記憶性を持つ理由の覚え方
$Geo$と$Exp$が無記憶性を持つのは、

• ベルヌーイ試行が成功する確率は直前のベルヌーイ試行の結果に依らないから
• ポアソン事象が発生する確率は直前のポアソン事象発生有無に依らないから

ベルヌーイ試行やポアソン事象の定義（分布一覧参照）から自明ですね。

各分布が再生性を持つ理由の覚え方

• “水色”の3つについてはいずれも “黄色”の和が従う分布だから
  例）$Bin(n,p)$は$Ber(p)$に従う$X_i$の和$S_n=\Sigma_{i=1}^n Xi$が従う分布である。
  $S_n$と$S_m$が共に${\sim}Bin$なら$S_n+S_m (=S_{n+m})$も当然${\sim}Bin$
• $N$については「正規分布の線形結合は正規分布」だから
• $Po$については、時刻に依らない変数の和は時刻に依らないから
  例）平均発生回数が時刻によって変化しない事象が2つあったとする。
  一方は1秒当たり平均2回、一方は1秒当たり平均5回発生するとする。
  2つの事象の発生回数の和は1秒当たり平均7回で、
  この平均発生回数は時刻によって変化しない。

期待値・分散を定義から計算する練習も必要

試験では定義に基づいて計算する問題も出題されます。
上の方で「他の分布から導けるものも多い」と書きましたが、
定義に基づいて期待値・分散を導出する練習もしておきましょう。

参考

（準備中・・・）
各分布についての補足事項などを別記事にまとめようかと検討中。
ご興味がある方はLGTMやフォローなどいただければと思います（励みになります）。