はじめに

意識のモデル化に興味があります。

そこで、物理学では外界をどのようにモデル化しているかが気になります。
というわけで、物理学のマクスウェル方程式について投稿します。

マクスウェル方程式は、電磁場（光を含む）を記述する古典電磁気学の基礎方程式です。
つぎの特徴があるようです。

物理学にはじめて「場（field）」概念を導入した。　電場、磁場、電磁場
方程式から電磁波の存在とその速度（光速の値）が導出できる
アインシュタインの特殊相対性理論と密接な関係がある

場（field）

空間座標が独立変数となっているような関数を場という。
関数値の型により、スカラー場、ベクトル場、スピノル場、またはテンソル場などがある。

場の例
磁束密度 $\bf {B}(t,x)$ ：磁束の単位面積当たりの面密度。ベクトル場。
単位は国際単位系 (SI) ではT(テスラ)、CGS単位系ではG(ガウス)

場は物理的実体を持つとみなされている。
粒子は場を作り、その場は他の粒子に作用する。そして、場は、エネルギーや運動量を持つ。

ベクトル微分演算 ∇（ナブラ、nabla）

ベクトル微分演算子$ \nabla$とは
$ \nabla ={\hat {\boldsymbol {x}}}{\frac {\partial }{\partial x}}+{\hat {\boldsymbol {y}}}{\frac {\partial }{\partial y}}+{\hat {\boldsymbol {z}}}{\frac {\partial }{\partial z}}$

ただし、${ {\hat {\boldsymbol {x}}},{\hat {\boldsymbol {y}}},{\hat {\boldsymbol {z}}}}$ はそれぞれ x, y, z 方向の単位ベクトル

$ \nabla = \sum _{{i=1}}^{n} {\hat {e}}^{i} {\frac {\partial }{\partial {x{i}}}} $ 　　　ただし　${\hat {e}}^{i}: 1\leq i\leq n $　は標準基底。

アインシュタインの和の規約では、$ \nabla = {\hat {e}}^{i} {\partial {{i}}} $

勾配(gradient)

スカラー場 $f $の勾配とは
$ \nabla f={\frac {\partial f}{\partial x}}{\hat {\boldsymbol {x}}}+{\frac {\partial f}{\partial y}}{\hat {\boldsymbol {y}}}+{\frac {\partial f}{\partial z}}{\hat {\boldsymbol {z}}}$

発散(divergence) 湧き出し

ベクトル場 ${ {\boldsymbol {v}}(x,y,z)=v_{x}{\hat {\boldsymbol {x}}}+v_{y}{\hat {\boldsymbol {y}}}+v_{z}{\hat {\boldsymbol {z}}}} $　の発散とは、
$\nabla \cdot {\boldsymbol {v}}={\frac {\partial v_{x}}{\partial x}}+{\frac {\partial v_{y}}{\partial y}}+{\frac {\partial v_{z}}{\partial z}}$

 \\
 =\lim_{V \to 0}　\frac {\oint \!\!\!\! \oint_S \boldsymbol {v} \cdot d\mathbf{S}} {V}\\
 =div　\boldsymbol {v}

回転(rotation)

ベクトル場 ${ {\boldsymbol {v}}(x,y,z)=v_{x}{\hat {\boldsymbol {x}}}+v_{y}{\hat {\boldsymbol {y}}}+v_{z}{\hat {\boldsymbol {z}}}} $　の回転とは、
$ \nabla \times {\boldsymbol {v}}=\left({\frac {\partial v_{z}}{\partial y}}-{\frac {\partial v_{y}}{\partial z}}\right){\hat {\boldsymbol {x}}}+\left({\frac {\partial v_{x}}{\partial z}}-{\frac {\partial v_{z}}{\partial x}}\right){\hat {\boldsymbol {y}}}+\left({\frac {\partial v_{y}}{\partial x}}-{\frac {\partial v_{x}}{\partial y}}\right){\hat {\boldsymbol {z}}}$

 |\nabla \cdot {\boldsymbol {v}}|
 =\lim_{\Delta S \to 0}　\frac { \oint_S \boldsymbol {v} \cdot d\mathbf{s}} {\Delta　S}\\
 =|rot　\boldsymbol {v}|  、方向は右ねじの規則で決まる

マックスウェル方程式（Maxwell's equations）

つぎの４つの等式をマックスウェル方程式という。

磁場の構造（磁束の湧き出しはない）　$\nabla \cdot \bf {B}(t,x) = 0 \tag{1} 　$
変化する磁束と電場　$\nabla \times \bf{E(t,x)} + \frac{\partial \bf{B(t,x)}}{\partial t} = 0\tag{2} $
電場の構造（電荷による電束の湧き出し）　$\nabla \cdot \bf{D(t,x)} = \rho(t,x)\tag{3} $
変化する電束と磁場　$\nabla \times \bf{H(t,x)} = \bf{j(t,x)}\tag{4} + \frac{\partial \bf{D(t,x)}}{\partial t} $

ここで$H$ は磁場の強度、$E$ は電場の強度、$B$ は磁束密度、$D$ は電束密度（変位電流）。
$ρ$ は電荷密度、$j$ は電流密度。

$\mu$ を透磁率、$\epsilon$ を誘電率、$\sigma$ を電導率とすると、つぎの関係がある　$B=\mu H$、$D=\epsilon E、j=\sigma E$

「$∇·$」、「$∇×$」はベクトル場の発散 (div) と回転 (rot) 。

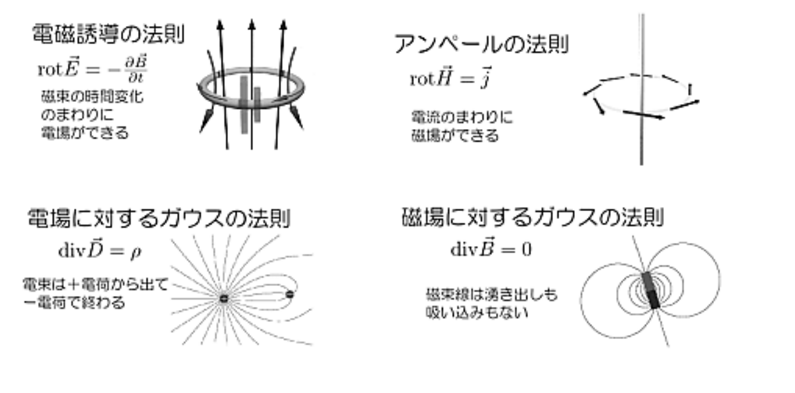
４つの等式の意味

（１）磁束は湧き出さない。N極とS極は必ずペアー。磁気単極子（モノポール）が存在しない。磁場に関するガウスの法則。
（２）電場は磁束変化より発生する。　ファラデーの電磁誘導の法則：$V= - \frac {\Delta \phi} {\Delta t}$
（３）電束は電荷により湧き出す。　電場に関するガウスの法則。またはクーロンの法則：$F = k\frac{q_A　q_B} {r^2} $　
（４）磁場は、変位電流と電流により発生する。　アンペールの法則：$ H = \frac{I} {2 \pi r}$

電磁気学の４つの法則をつぎに図示します。

マクスウェル方程式を１本にまとめたのは誰？
https://blog.goo.ne.jp/ktonegaw/e/226568b2c27822fb9fdfdb088e7018d3

光速ｃ

電磁波の速度を求めると、光速と一致する。この導出過程はつぎのようになる。

次を仮定する。電場$E$ は$x$成分のみ。電場$E$は$xy$平面で同一値、電荷と電流は無い。

透磁率 $\mu$、磁場の強さ $H$、磁束密度$B$ の関係「$B=\mu H$」で、マクスェル方程式（２）を書き換えると
$\nabla \times \bf{E(t,x)} +　\mu \frac{\partial \bf{H(t,x)}}{\partial t} = 0\tag{2-1} $

仮定より

$\frac{\partial {E_x}} {\partial z} + \mu \frac{\partial {H_y}} {\partial t} =0\tag{A}$

同様に$誘電率\epsilon$、電場の強度$E$、電束密度$D$ の関係「$D=\epsilon E$」でマクスェル方程式（４）を書き換えると

$\nabla \times \bf{H(t,x)} - \epsilon \frac{\partial \bf{E(t,x)}}{\partial t} = \bf{j(t,x)}\tag{4-1} $
仮定より

$\frac{\partial {H_y}} {\partial z} - \epsilon \frac{\partial {E_x}} {\partial t} =0\tag{B}$

式AとBは、$E_xとH_y$の連立方程式なので、$H_y$を消去すると。マクスウェルの波動方程式が求まる。

${{\frac {\partial ^{2}{\boldsymbol {E_x}}}{\partial z^{2}}}-\mu \epsilon {\frac {\partial ^{2}{\boldsymbol {E_x}}}{\partial t^{2}}}=0}$

波動方程式を解くと、角周波数$\omega$、波数$k$とすると。

$k^2 = \epsilon \mu \omega^2$

これより真空中では、　$v=\frac {\omega} {k}= \frac {1} {\sqrt{\epsilon_0 \mu_0 }} = = \frac {1} {\sqrt{8.85×10^{−12} F m^{−1} 1.25×10^{−6} N A^{−2} }}=3.006×10^8=c$

電磁波の波動方程式

電場と磁場は次の波動方程式を満たす。

${\displaystyle \nabla ^{2}{\boldsymbol {E}}-\mu \epsilon {\frac {\partial ^{2}{\boldsymbol {E}}}{\partial t^{2}}}=0}$

${\displaystyle \nabla ^{2}{\boldsymbol {B}}-\mu \epsilon {\frac {\partial ^{2}{\boldsymbol {B}}}{\partial t^{2}}}=0}$

電磁エネルギー

電磁場はつぎのエネルギーを持つ
$ U = \frac 1 2 E^2 + \frac 1 2 B^2 $

AM,FM アンテナ

AMバーアンテナ、微小ループアンテナは、磁場の変化による電圧を検出（電磁誘導による起電力）。　マクスウェル方程式(2)式
FM（ロッドアンテナ、ダイポール、ループアンテナ）は、電界の変化による電圧を検出します。

アインシュタインの特殊相対性理論との関係は

電磁場として電場と磁場の組ではなく、スカラーポテンシャルとベクトルポテンシャルの組を考えると
マクスウェル方程式は、つぎの１本の式で表現できるようです。
https://ja.wikipedia.org/wiki/マクスウェルの方程式#マクスウェルの方程式と特殊相対性理論

$\Box A^\mu -\partial^\mu\partial_\nu A^\nu=\mu_0 j^\mu$

ここで

$\Box=\frac{1}{c^2}\frac{\partial^2}{\partial t^2}-\frac{\partial^2}{\partial x^2}-\frac{\partial^2}{\partial y^2}-\frac{\partial^2}{\partial z^2}$　（ダランベール演算子）
$A^\mu$ は4元ポテンシャル、$j^\mu$ は4元電流密度　

おわりに

電場、磁場はマクスウェル方程式でモデル化される。マクスウェル方程式から電波の存在とその速度が光速であることが予言され、実験結果と整合した。

電磁場のモデル化順序は次のように考えられる。
（１）現象の把握：　磁石が鉄を引き寄せる、静電気が軽い物体を引き寄せる、電流による磁場生成、磁束変化による起電力発生
（２）物理量の特定と法則化：　磁場に対するガウスの法則、クーロンの法則、ファラデーの電磁誘導の法則、アンペールの法則
（３）新概念の導入：　ベクトル場（遠隔作用）、ベクトル微分演算∇
（４）定式化：　連立偏微分方程式でマクスウェル方程式を表出
（５）予言：　マクスウェル方程式から波動方程式の導出。電波の存在とその速度が光速であることを予言

意識のモデル化も同様の順序になる？
マクスウェル方程式に現れる単語と「意識」を組み合わせると、つぎのような、それらしいSF的な単語が生成できます。

意識場、意識束、意識荷、意識流
意識場の強度、意識束密度、意識荷密度、意識流密度
意識場の発散と回転と勾配、意識エネルギー、意識波（波長、速度、量子）

意識のモデル化まで先は長い。

参考　ウィキペディア

https://ja.wikipedia.org/wiki/場
 https://ja.wikipedia.org/wiki/ナブラ
 https://ja.wikipedia.org/wiki/マクスウェルの方程式
 https://ja.wikipedia.org/wiki/特殊相対性理論#マクスウェル方程式
 https://ja.wikipedia.org/wiki/4元電流密度
 https://ja.wikipedia.org/wiki/電磁場の量子化
 https://ja.wikipedia.org/wiki/電磁気学
 https://ja.wikipedia.org/wiki/ガウスの法則
 https://ja.wikipedia.org/wiki/ガウスの法則 (磁性)

参考　Web