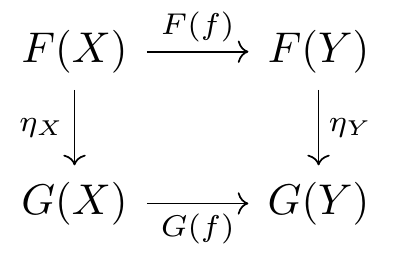はじめに

気になっていた圏論（category theory）について調べてみました。

圏論は、矢印(射)を使用する、抽象化のための数学言語です。
圏論は数学、数理物理学、プログラミング言語等で使用されています。
圏論で使われる概念のイメージをつぎに示します。

射　矢印や関係
圏　矢印を使用した世界のモデル
関手　圏の間の射。モデル間の変換
自然変換　関手の間の射

米国数学者ソーンダース・マックレーン（Saunders Mac Lane, 1909年8月4日 - 2005年4月14日）たちが、自然変換の概念を構築するために、圏論を創設したようです。

可換図式（commutative diagram）

始点と終点が同じである図式のすべての向き付きの道が合成によって同じ結果になるようなものである。
可換図式は代数学において方程式が果たすような役割を圏論において果たす。
図式は可換でないかもしれない、すなわち図式の異なる道の合成は同じ結果にならないかもしれないことに注意する。
破線の矢は一般に、図式の残りが成り立つときにはいつでもその射が存在する、という主張を表現する。

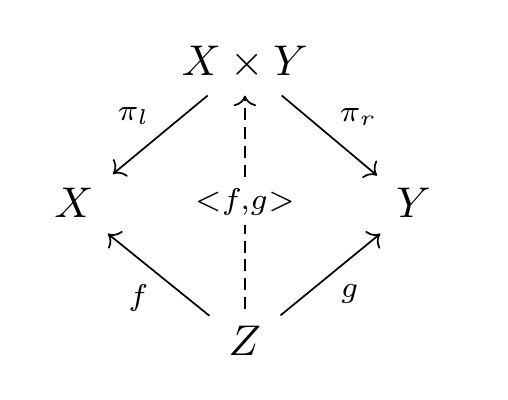
可換図式例　直積の圏論的定義
3つ組 $(X \times Y,\pi_l,\pi_r)$ が、$X,Y$ の積であるとは、つぎの図式を可換にすること。

圏（category）

（https://ja.wikipedia.org/wiki/圏 (数学)　より）

圏論では対象の記述をより一般的な射のことばで置き換える（対象は恒等射と同一視できる）。対象にこだわると見えなかった構造が見えてくる。圏の定義は集合をベースとしていない。逆に圏を土台にして公理的集合論を展開できる。

圏の定義

$圏 \boldsymbol C$は、４つ組 $\boldsymbol C=(O,A,∘,id)$ から成る。ここで

（１） $O$ は対象(Object)の集まり
（２） $A$ は射(arrow,morphismモルフィズム)の集まり。各対象$X,Y ∈ O $に対して、$A(X,Y)$は、$XからY$への射の集まりで $Hom_c(X,Y)$ と書く。 $f が、A(X,Y)$ の要素であることを、$f:X→Y$や $X\xrightarrow[]{ f }Y$ と書く。
（３） $∘$ は射の合成。２つの射　$X\xrightarrow[]{f}Y$　と　$Y\xrightarrow[]{g}Z$　があるとき、$f$ と $g$　を合成した射　$X\xrightarrow[]{g∘f}Z$　が存在する。ただし、任意の射 $X\xrightarrow[]{f}Y\xrightarrow[]{g}Z\xrightarrow[]{h}W$　について結合律　$h∘(g∘f) = (h∘g)∘f$ を満たす。
（４） $id$は恒等射(identity)。各対象 $X∈O$ に対して、恒等射 $id_X:X→X$　があり、任意の射 $f：X→Y$ に対して、$f = id_Y∘f = f∘id_X$

圏の例

身近な圏

路線図　対象を地名、射を接続とする。鉄道路線図など
血縁関係　対象を人、射を血縁関係とする。　射を親子関係とすると圏にならない（結合律、恒等射がない）。
モデル　対象をモデルの構成要素、射を構成要素の間の関係とする
設計図　対象を部品、射を部品の間の接続とする。家、自動車などの設計図
構築物　対象を部品、射を部品の間の接続とする。実際に建設や生産された家、自動車など
言語系　対象を単語、射を単語の間の関係
自然数　対象を自然数の集合 $N$、射を各自然数とする

圏の構造による圏

$\boldsymbol 0$（empty category）　対象と射が無い圏
$\boldsymbol 1$（terminal category or trivial category or final category）　１つの対象とその恒等射のみからなる圏
$\boldsymbol 2$ ２つの対象とその間の１つの射、恒等射とのみからなる圏
$\boldsymbol 3$ ３つの対象とその間の３つの射、恒等射のみからなる圏　f1:A→B、f2:B→C、f3:A→C
$\boldsymbol {Mon}$（モノイド、monoid）　対象がただひとつの圏、射は複数可。例：自然数の集合$N$が対象で、各自然数が射、合成を乗法とする
離散圏（Discrete category）　恒等射以外の射を持たない圏。離散圏は対象のクラスと同じ。各対象が他の対象から孤立
双対圏（dual category、opposite category）　圏 $\boldsymbol C$ の射の向きを逆にした圏で $\boldsymbol C^{op}$ と書く。 $({\boldsymbol C}^{op})^{op} = \boldsymbol C$

数学的構造の圏

$\boldsymbol {Set}$　集合の圏：　対象は集合、射は写像 $f$、射の合成 $g∘f$ は合成写像 $g(f(x))$、恒等射 $id_X$ は $f(x)=x$ で集合 $X$ 上の恒等写像
$\boldsymbol {Grp}$　群の圏：対象は群、射は群準同型写像。群準同型写像 $h: G → H とは (G, ∗) と (H, ⋅) $を２つの群としたとき、 $h(u*v)=h(u)\cdot h(v) \ \ \ (\forall u,v\in G)$ を満たす写像。
$\boldsymbol {Ab}$　アーベル群の圏：対象はアーベル群
$\boldsymbol {Ring}$　環の圏：対象は環、射は環準同型写像
$\boldsymbol {CRing}$　可換環の圏
$\boldsymbol {Field}$　体の圏
$\boldsymbol {Vect_k}$　線形空間の圏：対象は体k上の線形空間、射は線形写像
$\boldsymbol {Top}$　位相空間の圏：対象は位相空間、射は連続写像

Haskell の圏

$\boldsymbol {Hask}$　Haskell の圏：対象は Haskell の型、射は Haskell 関数、射の合成は Haskell 関数合成 (.)、恒等射は Haskell 恒等関数 id。関数合成(.)と恒等関数 id の Haskell 型をつぎに示す。

(.) :: (b -> c) -> (a -> b) -> a -> c
id :: a -> a

その他の圏

小さい圏の圏 $\boldsymbol Cat$ （category of small categories）すべての小さい圏を対象とし、圏の間の関手を射とする圏である。実際には、Cat は自然変換を二次元の射(2-射) とする二次圏（(2-圏) を成すものと見なせる。Cat の始対象は対象も射も持たない空圏 0 であり、終対象はただ一つの対象とただ一つの射（恒等射）のみからなる圏 1である。小さい圏の圏 Cat それ自身は大きい圏であり、それゆえ自身を対象として含むことはない。
デカルト閉圏（CCC:cartesian closed category）　直観主義論理、単純型付ラムダ計算、デカルト閉圏の間の深い同型を与える。トポスという種類のデカルト閉圏は、従来の集合論に替わる一般的な枠組みとして提示される。
豊穣圏（enriched category）　（局所的に小さい）圏における射集合を一般のモノイド圏の対象に置き換えて得られる圏の一般化

始対象と終対象

圏 𝒞 の始対象（initial object, coterminal object）とは、𝒞 の任意の対象 X に対してちょうど一つの射 I → X が存在するような 𝒞 の対象 I のことを指す。
圏 𝒞 の終対象（final object, terminal object）とは、始対象の双対概念であり、 𝒞 の任意の対象 X に対してちょうど一つの射 X → T が存在するような 𝒞 の対象 T のことを指す。

関手（functor）

（「圏・関手・自然変換　～ベーシック圏論をゆるく読む会の記録2018～」より）

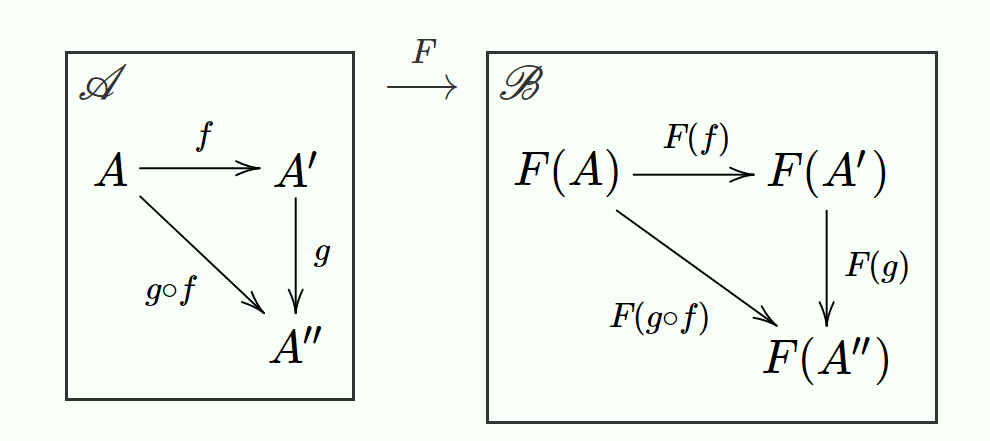
圏 $\boldsymbol C$ から圏 $\boldsymbol D$への射を関手 $F:C→D$ という。

関手の定義　共変関手（covariant functor）

圏 $\boldsymbol C$ から圏 $\boldsymbol D$ への（共変）関手 $F:\boldsymbol C→\boldsymbol D$ は、

$\boldsymbol C$ の各対象 $X$ を $\boldsymbol D$ の各対象 $F(X)$ に対応させ、$\boldsymbol C$ における射 $f: X → Y$ を $\boldsymbol D$ における射 $F(f): F(X) → F(Y)$ に対応させる。以下の性質を満たす
各対象 $X ∈ \boldsymbol C$ に対して $F(id_X) = id_{F(X)}$ ,任意の射 $f: X → Y $および $g: Y → Z$ に対して $F(g ∘ f) = F(g) ∘ F(f)$
すなわち、関手に対して恒等射および射の合成を保存することが要請される。関手 $F:\boldsymbol C→\boldsymbol D$　は圏 $\boldsymbol C$ における可換図式を、圏 $\boldsymbol D$ における可換図式へ移す。

関手の例

身近な関手

生産　設計図から生産物への関手
喩えや解釈　知らない事柄からよく知っている事柄への関手　
翻訳　日本語から英語への関手
コンパイル　言語Aプログラムから言語Bプログラムへの関手

関手の構造による関手

恒等関手（identity functor）　圏 $\boldsymbol C$の恒等関手 $\boldsymbol 1_C$ とは、どの対象と射もそれ自身へうつす関手
反変関手（contravariant functor）　圏 $\boldsymbol C$ を圏 $\boldsymbol D$ の双対圏 $\boldsymbol D^{op}$ に移す関手。射の向きを変える関手
自己関手（endofunctor）　圏 $\boldsymbol C$ から同じ圏 $\boldsymbol C$ への関手
定関手（constant functor、selection functor）　圏 $\boldsymbol D$ の対象 $X$ について、圏 $\boldsymbol C$ のすべての対象を $X$ に移し、$\boldsymbol C$ の全ての射を $X$ の恒等射に移す関手

忘却関手と自由関手（forgetful functor、free functor）

圏 $\boldsymbol C$ が、圏 $\boldsymbol D$ の対象のうちでさらに付加的な構造を持つ圏として定式化されているとする。
$\boldsymbol C$ の対象の付加的な構造を無視する関手を、圏 $\boldsymbol C$ から圏 $\boldsymbol D$ への忘却関手という。

$U:\boldsymbol {Grp} \rightarrow \boldsymbol {Set}$ 　群$G$について、$U(G)$ は $G$ の台集合、群準同型写像 $f:G→H$ について、$U(f)$ は写像 $f$ 自身。$U$ は群の構造を忘れる。射が群準同型写像であることを忘れる
$U:\boldsymbol {Ring} \rightarrow \boldsymbol {Set}$ 　環の構造を忘れる関手
$U:\boldsymbol {Vect_k} \rightarrow \boldsymbol {Set}$ 　線形空間の線形構造を忘れる関手
$U:\boldsymbol {Ring} \rightarrow \boldsymbol {Mon}$ 　環の加法構造は忘れるが、台となる乗法のモノイドは覚えている関手。環 $R$ について$U(R)$ は集合 $R$ で、$・$と$１$によりモノイドになる
$U:\boldsymbol {Ring} \rightarrow \boldsymbol {Ab}$ 　環の乗法構造は忘れるが、台となる加法群は覚えている関手
$U:\boldsymbol {Ab} \rightarrow \boldsymbol {Grp}$ 　アーベル群が可換であることを忘れる。性質を忘れる。

$\boldsymbol C$ の対象に必要な付加的な構造を追加する関手を、圏 $\boldsymbol C$ から圏 $\boldsymbol D$ への自由関手$F:\boldsymbol {C} \rightarrow \boldsymbol {D}$ という。忘却関手の双対である。

$F:\boldsymbol {Set} \rightarrow \boldsymbol {Grp}$ 　集合から群をつくる関手
集合 $S$ について、$S$ 上の自由群（free group） $F(S)$ を構成できる。自由群とは、群の公理から必然的に従うこと以外は何の性質ももたない群である。直観的には群 $F(S)$ は、集合 $S$ に群になるのに十分なだけの新しい元を追加し、群の公理から強制される以外の方程式は何も課さないことで得られる。
$F:\boldsymbol {Set} \rightarrow \boldsymbol {CRing}$ 　集合から可換環をつくる関手
$F:\boldsymbol {Set} \rightarrow \boldsymbol {Vect_k}$ 　集合から、それを基底とする線形空間をつくる関手

Hom関手（Hom functor）

圏 $\boldsymbol C$ から $\boldsymbol Set$ へのHom関手 $h_A= Hom(A,-)$ をつぎのように定める。
対象 $X$ に対して、$h_A(X) = Hom_C(A,X)$。
射 $f:X→Y$ に対して、$Hom_C(A,X) \xrightarrow[]{ h_A(f) } Hom_C(A,Y)$ 。これを $h_A(f)= Hom(A,f)$と表記する。
ただし $a∈Hom_C(A,X)$ について $h_A(a) = f○a$ 。

その他の関手

表現可能関手（representablel functor）　圏 $C$ から圏 $Set$ への関手。米田の補題によって表現可能関手たちとその間の自然変換はもとの圏の構造を完全に反映している

自然変換（natural transformation）

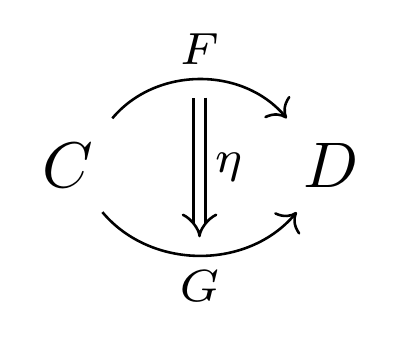
関手の間の射として自然変換 $\eta$ が得られる。
歴史的には、図形世界から代数世界への関手（翻訳）が乱立し、全然違うのに本質的に同じだった。その同じさを取り扱うために、自然同値（可逆な自然変換）を定義する必要があった。

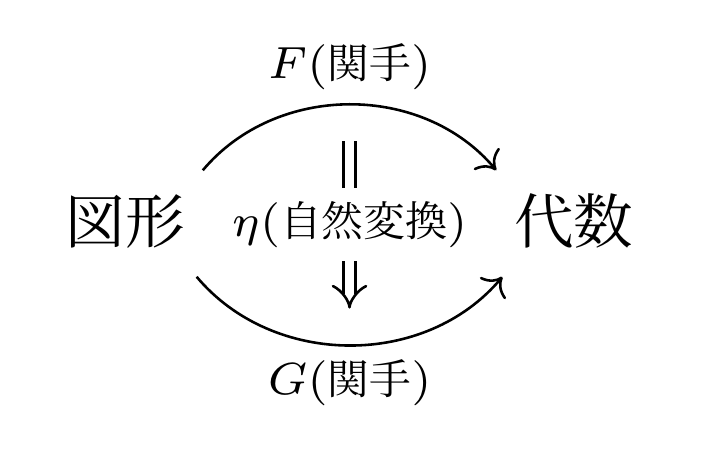
自然変換の定義

$F$ および $G$ を圏 $\boldsymbol C$ から $\boldsymbol D$ への関手とする。$\eta$ が $F$ から $G$ への 自然変換 であるとは、つぎの条件をみたすときである。
$\eta$ は $\boldsymbol C$ の各対象 $X$ に対して射 $\eta_X :F(X)→G(X)$ を対応させる
圏 $\boldsymbol C$ の任意の対象 $X,Y$ および任意の射 $f:X→Y$ に対して、$G(f)○\eta_X$　=　$\eta_Y○F(f)$ が成り立つ。
このとき、$\eta:F⇒G$ と書く。また $\eta_X$ を $\eta$ の $X$ 成分と呼ぶ。

この自然変換 $\eta$ の定義は、圏 $\boldsymbol D$ 上の可換図式としてつぎのように書ける。
ここで圏 $\boldsymbol C$ で　$f:X→Y$、関手 $F,G$ ：$\boldsymbol C→\boldsymbol D$

自然変換 $\eta$ は、$\boldsymbol D$ の射 $\eta_X:F(X)→G(X)$ を束ねたもの。
自然変換という高次の矢印が、低次の射を束ねたもので書けている。

自然変換の例

図形から代数への関手の間の変換
行列式
Haskell のモナド　モナドで計算効果と計算を分離し参照透過性を維持
座標変換　およそ数学における「準同型」というのは，自然変換になっている
フーリエ変換

関手圏(functor category)

$\boldsymbol C$ を小さい圏とし（すなわち対象たちや射たちは真クラスではなく集合をなす）、 $\boldsymbol D$ を任意の圏とする。
つぎの圏を考えることができる。これを関手圏とよびFun(C, D)、Funct(C, D)、[C, D]、${\boldsymbol D}^{\boldsymbol C}$などと表記する。

対象: $\boldsymbol C$から$\boldsymbol D$への関手
射: 自然変換
射の合成: 自然変換の合成

抽象化と同じさ

抽象化とは、異なるものごとの間に、同じさを持ち込むことです。
例えば、ネコ、魚、人間は、抽象化するとすべて同じで、生物になります。
抽象化では個々の対象から離れて、生物という構造を考えています。

同型（isomorphic）　A ≅ B

射 $f:A→B$ が可逆（invertible）であるとは、つぎを満たす射 $g:B→A$ が存在すること。
$g○f = 1_A $、$f○g = 1_B $
このとき、$g$ を $f$ の逆射（inverse）と呼び、$f^{-1}$ と書く。可逆な射を同型射（isomorphism）と呼ぶ。
対象 $A$ から $B$ への射が同型射であるとき、$A$ と $B$ は同型（isomorphic）といい、$A ≅ B$ と表記する。
２つの対象 $A$ と $B$ が同型ならば、２つは等しくないが、２つの射 $f,g$ の合成で元にもどれる。

「圏の圏」において、可逆な関手が存在することで、圏の同型が定まる。
群はモノイド（対象がただ１つの圏）で、すべての射が同型射である圏である。

自然同値（natural Equivalence）、自然同型 (naturally isomorphic)

圏 $\boldsymbol C$ から圏 $\boldsymbol D$ への関手を対象とし、それらの間の自然変換を射とする圏を、圏 $\boldsymbol C$ から圏 $\boldsymbol D$ への関手圏（functor category）と呼び、$Fun(\boldsymbol C,\boldsymbol D)$ と書く。

関手圏の射としての同型射であるような自然変換を自然同値という。
関手圏の対象として同型であるような２つの関手を自然同値であるという。（あるいは自然同型もしくは関手の同型ともいう）

圏同値 (categorically equivalent)

圏同値は２つの圏が、自然変換の意味で本質的には同じであることを意味する。
２つの逆向きの関手 $F:C→D$、 $G：D→C$ を考える。$G○F$ $≅$ $1_C$、$F○G$ $≅$ $1_D$　で恒等関手と同型になるとき、圏 $C,D$ は圏同値である。
圏の同型では、$G○F$ や $F○G$ は恒等関手に等しい必要があった。この「$＝$」を関手圏の同型「≅」（可逆な自然変換）で置き換えたものが圏同値。

おわりに

圏論は関係の構造に注目し、シンプルで良い感じです。対象自体に重きをおかず、関係（射）に注目する。
仏教の諸法無我、全てのものは関係によって生じたものであって実体がないと整合性がありそうです。

謎が多い「意識」に対して、圏論が使えるか？　意識の実体ではなく、意識の間の関係についての記述が可能か？

参考　ウィキペディア

https://ja.wikipedia.org/wiki/圏論
 https://ja.wikipedia.org/wiki/圏 (数学)
https://ja.wikipedia.org/wiki/射 (圏論)
https://ja.wikipedia.org/wiki/関手
 https://ja.wikipedia.org/wiki/自然変換
 https://ja.wikipedia.org/wiki/モノイド
 https://ja.wikipedia.org/wiki/モノイド圏
 https://ja.wikipedia.org/wiki/モナド (圏論)

https://ja.wikipedia.org/wiki/圏同値　　　
 https://en.wikipedia.org/wiki/Equivalence_of_categories
https://en.wikipedia.org/wiki/Isomorphism_of_categories

https://ja.wikipedia.org/wiki/図式 (圏論)
https://ja.wikipedia.org/wiki/可換図式

参考資料　

ニコニコ大百科　圏論
https://dic.nicovideo.jp/a/圏論

『圏論の道案内』3　
https://ameblo.jp/karaokegurui/entry-12543373701.html

圏・関手・自然変換　～ベーシック圏論をゆるく読む会の記録2018～
https://corollary2525.hatenablog.com/entry/2018/11/23/235900

圏論による意識の理解（土谷尚嗣、西郷甲矢人）
https://www.jstage.jst.go.jp/article/jcss/26/4/26_462/_article/-char/ja/ https://ja.wikipedia.org/wiki/Haskell

圏論とは何か
https://infinitytopos.wordpress.com/2015/01/25/圏論とは何か

自然知能と圏論　西郷　甲矢人
http://www.inter.ipc.i.u-tokyo.ac.jp/pdf/saigo.pdf

『圏論の道案内』発売記念西郷甲矢人先生講演会レポート
https://gihyo.jp/science/serial/01/category_theory_report/0002

圏論とプログラミング稲見泰宏
https://speakerdeck.com/inamiy/category-theory-and-programming

参考書籍

圏論の道案内 ~矢印でえがく数学の世界 2019/8/9 西郷甲矢人, 能美十三
圏論の歩き方 2015/9/9 圏論の歩き方委員会
もっとも美しい対称性 2008/10/16 イアン・スチュアート
心はすべて数学である 2015/12/9 津田一郎

参考動画

圏論勉強会@ワークスアプリケーションズ中村晃一
https://www.youtube.com/watch?v=Af8Vf_QUmXA&list=PLzJWjr7AvxH37O6GPqx20NpF0HaSrndVc
http://nineties.github.io/category-seminar/#/
2013年圏論勉強会資料
第1回:圏論って何?
第2回:モノイド・群
第3回:様々な圏
第4回:射で考える
第5回:様々な射
第6回:積・余積・極限
第7回:様々な極限,代数的データ型
第8回:ω余極限,連続性,プログラム運算
第9回:領域理論・不動点意味論
第10回:始代数・終余代数と不動点,型函手
第11回:指数対象・デカルト閉圏
第12回:自然性・米田の補題
第13回:随伴・モナド

教科書

圏論の基礎(CWM) 2012/7/17 S. マックレーン、Categories for the Working Mathematician 1971/1/1 Saunders MacLane
ベーシック圏論普遍性からの速習コース 2017/1/29 Tom Leinster、Basic Category Theory
圏論原著第2版 2015/9/19スティーブアウディ、Category Theory
Category Theory STEVE AWODEY, https://www.andrew.cmu.edu/course/80-413-713/notes/
数学その形式と機能 1992/4/1 S. マックレーン、Mathematics, Form and Function

その他

Basic Category Theory for Computer Scientists 1991/8/7 Benjamin C. Pierce
Computational Category Theory 1988/11/1 D. E. Rydeheard, Burstall

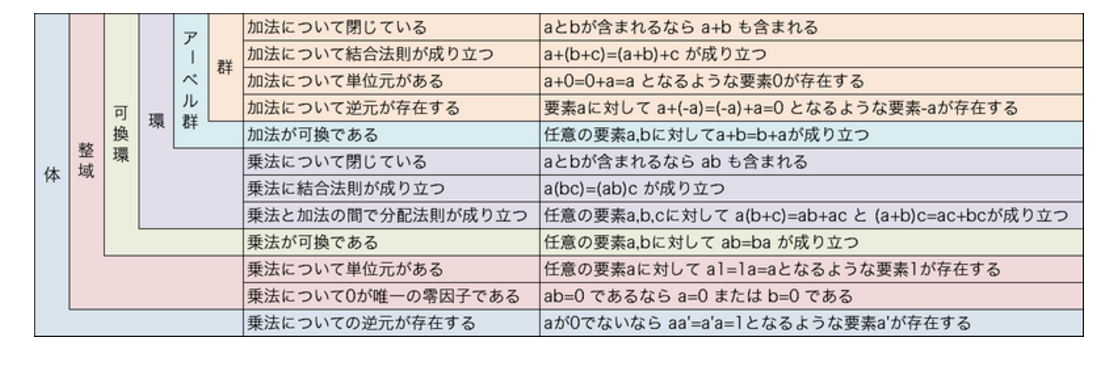
付録１　群、環、体

大人になってからの再学習より　http://zellij.hatenablog.com/entry/20121211/p1

始域や終域が空集合の写像｜空関数と単射性と全射性
https://sorai-note.com/math/empty-function/

圏論ってナンだ？ (１) 抽象化のための言語

はじめに

可換図式（commutative diagram）

圏（category）

圏の定義

圏の例

身近な圏

圏の構造による圏

数学的構造の圏

Haskell の圏

その他の圏

始対象と終対象

関手（functor）

関手の定義 共変関手（covariant functor）

関手の例

身近な関手

関手の構造による関手

忘却関手と自由関手（forgetful functor、free functor）

Hom関手（Hom functor）

その他の関手

自然変換（natural transformation）

自然変換の定義

自然変換の例

関手圏(functor category)

抽象化と同じさ

同型（isomorphic） A ≅ B

自然同値（natural Equivalence）、自然同型 (naturally isomorphic)

圏同値 (categorically equivalent)

おわりに

参考 ウィキペディア

参考資料

参考書籍

参考動画

教科書

その他

付録１ 群、環、体

関手の定義　共変関手（covariant functor）

同型（isomorphic）　A ≅ B

参考　ウィキペディア

参考資料　

付録１　群、環、体