2020年12月20日(日)の秋ロボ勉強会(Zoom使用)で発表予定です。
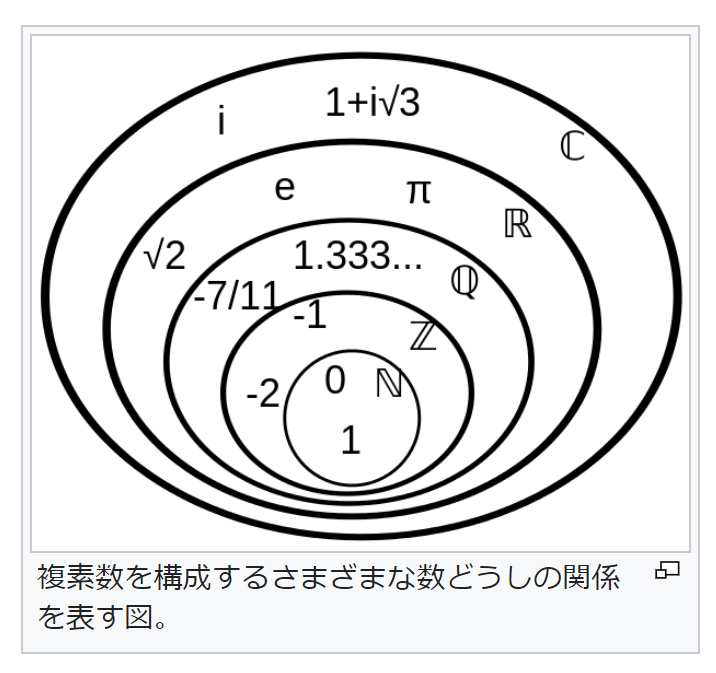
(https://ja.wikipedia.org/wiki/数 より)
はじめに
日頃何気なく使用している数の特徴について、調べてみました。
人類は数体系(Number system)を、制限を取り除くことにより、つぎのように拡張してきました。
数体系は無限概念と密接に結びついています。
我々と違う環境で生まれた知性体も同じような数体系の拡張を行うか?人類より進んだ文明の数体系はどうなっているか?
- 数の芽生え {1,2,たくさん} 幼児、チンパンジー
- $N$ 自然数(全体の集合 無限、可算無限濃度 $ℵ_0$
- $Z$ 整数(全体の集合)
- $Q$ 有理数(全体の集合)稠密順序集合、隙間があり連続性はない
- $R$ 実数(全体の集合) 連続、連続体濃度 $2^{ℵ_0}$、自然科学,工学で使用
- $C$ 複素数(全体の集合) $ i^2 = -1$ という不思議な虚数単位 $i$ 、工学で使用
- $H$ 四元数(全体の集合)マクスウェル方程式が一本の微分方程式になる
- $O$ 八元数(全体の集合)素粒子論等の物理学で使用
- $S$ 十六元数(全体の集合)
- ベクトル
- 行列 線型変換(回転、鏡映、拡大・縮小、剪断、これらの任意の合成)を表現する
- テンソル 相対性理論で使用
一般には、数概念は集合の上に構築されます。数の実体は集合ということです。
さらに、集合が実体ではなく、対象間の射という関係が実体だという圏論も良い感じです。
N 自然数(natural number)
特徴
- 個数、もしくは順番を表す
- 数論などでは1ではじまる $N_1$。 集合論と論理学では0から始まる $N_0 = {0,1,2,...} $
- 加法、乗法について閉じる。 $a+b, a*b ∈N$
- 単純なペアノの公理系から豊かな数論、素数論が展開される
ペアノの公理(Peano axioms)
自然数を厳密に定義したペアノの公理をつぎに示す。
自然数は次の5条件を満たす
- 自然数 0 が存在する
- 任意の自然数 a にはその後者 (successor)、suc(a) が存在する
- $0$ はいかなる自然数の後者でもない
- 異なる自然数は異なる後者を持つ: $a ≠ b ⇒ suc(a) ≠ suc(b) $
- $0$ がある性質を満たし、a がある性質を満たせばその後者 $suc(a) $ もその性質を満たすとき、すべての自然数はその性質を満たす
この単純な公理から、数論、素数論が展開されるのは驚き。リーマン予想(素数の分布についての予想)は、100万ドルの賞金がかかった未解決問題。
ジョン・フォン・ノイマンの構成法
つぎのように、集合論における標準的な構成によって、ペアノの公理を満たす集合が存在することを示せる。
任意の集合 $a$ の後者 $suc(a):=a ∪ \{a\} $と定義する
0 := {}
1 := suc(0) = 0 U {0} = {0}
2 := suc(1) = 1 U {1} = {0} U {{0}} = {0,{0}}
3 := suc(2) = 2 U {2} = {0,{0}} U {{0,{0}}} = {0, {0}, {0, {0}}}
...
可算濃度 アレフゼロ(aleph-zero)
アレフ数は無限集合の濃度を表す。
$N$ の要素の個数(濃度)を可算無限濃度または単に可算濃度といい $ℵ_0$(アレフ ゼロ:aleph-zero)と表記する。
次に大きい濃度がアレフ・ワン ℵ1、その次はアレフ・ツー ℵ2 と以下同様に続く。
自然数の1次元と2次元は一対一対応
自然数の1次元と2次元は、つぎのように一対一対応可能である。
$1,2,3,4,... ⇔ (0,0),(1,0),(1,1),(2,1),(2,2),... $
基数(cardinal number又はcardinal)と順序数(ordinal number)
- 基数 「一対一対応」原理。 $ \{a,b,c,d,e\}と\{x,y,z\}$の基数(集合の要素の数)は前者が大きい。数えるのではなく一対一対応で判定する。
- 序数 「次の数がある」原理。 数える行為。
その他
- 5世紀頃にインドで数としての「$0$」の概念が確立された
- 位取り記数法が広まったのは16世紀頃
- 圏論では、各自然数をそれぞれ射、和を射の合成、恒等射を 0 として圏を作成できる
Z 整数(integer)
特徴
- 整数は自然数の組で表現できる。 $(a,b)$ を $a-b$ と解釈する
- 加法について逆元がある。 $a + (−a) = 0$
- 可算濃度 $ℵ_0$。$N$ と $Z$ は一対一対応
- Python3.xの int 型は多倍長整数。動的にメモリを確保する
部分と全体は一対一対応する
部分の要素数が全体の要素数より小さくなるのは、有限集合の性質である。
$NはZ$の部分である。これらはつぎのように一対一対応する
$1,2,3,4,... ⇔ 0,1,-1,2,-2,... $
Q 有理数(rational number)
特徴
- 有理数は自然数の三組で表現できる。 $(a,b,c)$ を $a /(b-c)$ と解釈する
- 乗法について逆元がある (0を除く)。 $a*(1/a) = 1$
- 可算濃度 $ℵ_0$
-
稠密順序集合 $\forall x \forall y \ \ {x<y} \Rightarrow (\exists z \ \ x<z \ \land \ z<y) $
有理数がぎっしり詰まって連続に見えるが錯覚で、実は隙間がたくさんある - 有理数は、有限小数か有限な長さの循環節をもつ循環小数で表現できる
- Python 3.6.4 では、Fraction コンストラクタが用意されている
from fractions import Fraction
a = Fraction(1, 3)
b = Fraction(0.5)
c = a*b
print(a,b,c) # 1/3 1/2 1/6
R 実数(real number)
特徴
- 連続性がある、完備性とも言われる
- 自然科学における連続的なものの計測値を表すのに十分な数の体系だと考えられている
- 無理数を含む。 無理数とは、 $\sqrt2, π, e(ネイピア数)$など, 有理数で表せない数
- 連続体濃度 $2^{ℵ_0}$。$NとR$ は一対一対応できない事が背理法で証明できる。 連続体仮説 $2^{ℵ_0}=ℵ1$
無理数の分類(irrational number)
- 代数的数(algebraic number): $\sqrt2$など、有理数係数のn次方程式の解になる数。 可算濃度 $ℵ_0$。
- 超越数(transcendental number): $π,e$など、代数的数でない数。 $π+e$ は超越数かどうか分かっていない。 連続体濃度 $2^{ℵ_0}$
連続性、完備性 (continuity、completeness)
連続性には、複数の同値な定義がある。デデキント切断による定義はつぎのようになる。
全順序集合 K を、一方が他方の全ての元よりも小であるような二つの組に分けたとする。
K = A ∪ B、A,B ≠ ∅、(a ∈ A, b ∈ B ⇒ a < b)
このような組 (A, B) をデデキント切断(Dedekind cut)という。
$Q$ の切断を与えることで、切断に対応する実数をただ一つ定めることができる。
一般に全順序集合の切断には、つぎの四つの場合が考えられる。
- 下組の最大元と上組の最小元がある。
- 下組には最大元があるが、上組に最小元がない。
- 上組には最小元があるが、下組に最大元がない。
- 下組の最大元がなく、上組の最小元もはない。
各場合はつぎのように解釈できる。
- 有理数に稠密性があるため、この切断は不可能。
- 最大元にあたる有理数に対応
- 最小元にあたる有理数に対応
- 無理数に対応
こうして作成した $R$ に対して切断を行った場合、場合4.は不可能になり、場合2.と3.のいづれかになり、対応する境界の元がただ1つ決まる。
短い直線と長い直線は一対一対応
$1次元上の短い直線Sの両端を原点0と1とし、1次元上の長い直線Lの両端を原点0と a とする。$
$S 上の点 x と L 上の点 y は、つぎの関係で一対一対応する。$
$y = ax$
実数の1次元と2次元は一対一対応
実数直線と実数平面は一対一対応可能。つぎのように一対一対応を構成できる。
任意の2次元座標$(a,b)、 0\ ≦\ a,b\ <\ 1 $ を考える。
$a,b$ の小数点表示をつぎのように仮定する。
$a = 0.a_1 a_2 a_3...$
$b = 0.b_1 b_2 b_3...$
一対一対応する、一次元の座標 $c$ をつぎのように定める。
$c = 0.a_1 b_1 a_2 b_2 a_3 b_3$、 $0\ ≦\ c\ <\ 1 $
多次元空間でも1次元と同じ連続体濃度$2^{ℵ_0}$
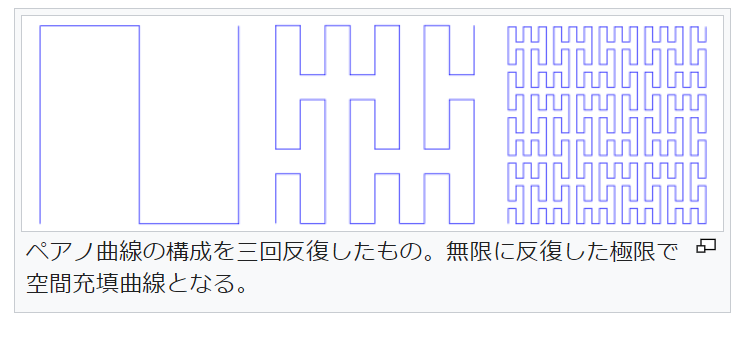
ペアノ曲線(Peano curve)空間充填曲線(space-filling curve)
1つの曲線で2次元平面を埋め尽くすことができる
計算可能数(computable number)
(https://ja.wikipedia.org/wiki/計算可能解析学 より)
計算可能数は実数であって、有限かつ停止するアルゴリズムによって、どんな望みの精度でも計算できるようなもの。
再帰的数(帰納的数、recursive number)あるいは計算可能実数(computable reals)とも呼ばれる。
数学の構成主義と関係する。
構成主義は、実際に構成できないため背理法(命題の偽を仮定して矛盾を導き、命題を証明する)を認めない。
計算可能数には、すべての代数的数および多くの超越数が含まれる。
計算可能数でない超越数には何がある?
C 複素数(complex number)
複素数は、実数を拡張した数体系であり、虚数単位 $i$ を用いて
$a + bi $
と表せる数のことである。ここで、$a, b$ は実数であり、$i^{2}=-1$ である。$ i= + \sqrt {-1}$
特徴
-
任意の2次方程式 $ax^2 + bx + c = 0 $が、解を持つためには複素数が必要。
解の公式 $ x=\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a} $ で $b^{2}-4ac$ が負の場合に複素数が必要になる。 -
複素数$a + bi $は2次元平面座標$(a,b)$と幾何学的に解釈できる。
この解釈で $i$倍は平面上の90度左回転とみなせ、$i^2=-1、i^4=1$となる。
この解釈により、$i=\sqrt {-1} $ は、広く受け入れらた。 -
Pythonはcomplex型を標準で用意
a = 1 + 2j
b = 3 + 4j
c = a*b
print(a,b,c) # (1+2j) (3+4j) (-5+10j)
複素数の和と積
和: $(a+bi) + (c+di) = (a+c) + (b+d)i$
積: $(a+bi) (c+di) = (ac-bd) + (bc+ad)i$
2次元ベクトルの和と積
2次元ベクトルの和と積は、複素数と異なる。
和: $(a,b) + (c,d) = (a+c, \ b+d) $
内積: $(a,b)・(c,d) = ac+bd = |(a,b)|\ |(c,d)| \cos(\theta)$ (inner product、またはスカラー積 scalar product)
外積: $(a,b) \times (c,d) = ad -bc = |(a,b)|\ |(c,d)| \sin(\theta)$ (outer product、または直積 direct product)
H 四元数(quaternion)
四元数(しげんすう)とは、複素数を拡張した数体系であり、虚数単位 $i, j, k$ を用いて
$a + bi + cj + dk$
と表せる数のことである。ここで、$a, b, c, d$ は実数であり、$i^{2}=j^{2}=k^{2}=ijk=-1$である。このとき $1, i, j, k$ は実数体上線型独立である。
特徴
- 積について非可換である。 ab ≠ ba
- 四元数による3次元の回転(姿勢)の表現は、3次正方行列による表現と比べて記憶容量が小さくて演算が高速。
CG、姿勢制御、信号処理、物理学で利用される - 物理学と関係する。マクスウェルの方程式は四元数変数のポテンシャル函数を用いて一本の微分方程式として表現できる
- Python の四元数ライブラリとして、 pyquaternion、numpy-quaternion 等がある
O 八元数(octonion)
特徴
- 乗法は非可換かつ非結合的。 ab ≠ ba、 a(bc) ≠ (ab)c
- 弦理論、量子理論で使用されている
- 例外型リー群 E8 248 次元多様体と関係し、素粒子物理学で注目されている
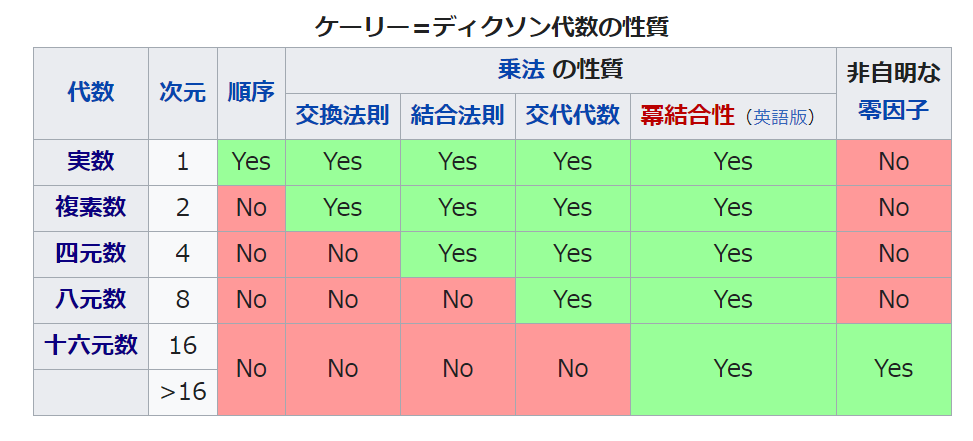
多元数(hypercomplex number; 超複素数)
有限次元実多元体は四種類(実数体 ℝ, 複素数体 ℂ, 四元数体 ℍ, 八元数体 𝕆)に限る。
実数係数 $a0, …, an−1$ を用いて基底 ${1, i1, …, in−1}$ に対する一次結合
$a_{0} 1 + a_{1}i_{1} + … + a_{n-1} i_{n-1}$
の形に書き表される。可能ならば、各基点元 $i_k$ に対して、その平方 $ {i_k}^2$ は −1, 0, 1 のうちの何れかから選ぶ。
ベクトル(vector)
- 和とスカラー倍を取る事ができる(線形性)
- ベクトル同士の積であるベクトル積(vector product)がある (クロス積、外積とも呼ばれる)
行列(matrix)
- 和、スカラー倍、乗法ができる
- 積は結合的で分配的だが、可換でない。 $a(bc) = (ab)c、 (a+b)c = ac + bc、 ab ≠ ba$
- 転地、行列式、固有値、逆行列などの演算がある
テンソル(tensor)
基底を選べば、多次元の配列として表現できるもの。テンソル自身は、特定の座標系によらないで定まる対象。
階数0のテンソル:スカラー
階数1のテンソル:ベクトル
階数2のテンソル:行列
階数Nのテンソル:N次元行列
おわりに
数には驚きが多い。
人類と異なる数体系を採用した知性体はいるのだろうか?
デジタル知性体は、計算可能数や構成主義的な数学と親和性が高いと考えられる。
この世界も我々もコンピュータシミュレーションであるという「シミュレーション仮説」があります。
これが正しいとすると、我々の数体系とシミュレーションモデルの数体系の関係が気になる。
参考 ウィキペディア
https://ja.wikipedia.org/wiki/数
https://en.wikipedia.org/wiki/Number#Classification
https://ja.wikipedia.org/wiki/自然数
https://ja.wikipedia.org/wiki/整数
https://ja.wikipedia.org/wiki/有理数
https://ja.wikipedia.org/wiki/実数
https://ja.wikipedia.org/wiki/超実数
https://ja.wikipedia.org/wiki/複素数
https://ja.wikipedia.org/wiki/四元数
https://ja.wikipedia.org/wiki/八元数
https://ja.wikipedia.org/wiki/十六元数
https://ja.wikipedia.org/wiki/多元数
https://ja.wikipedia.org/wiki/ケーリー=ディクソンの構成法
https://ja.wikipedia.org/wiki/分解型複素数
https://ja.wikipedia.org/wiki/分解型八元数
https://ja.wikipedia.org/wiki/デデキント切断
https://ja.wikipedia.org/wiki/数論
https://ja.wikipedia.org/wiki/素数
https://ja.wikipedia.org/wiki/リー群
https://ja.wikipedia.org/wiki/単純リー群
https://ja.wikipedia.org/wiki/無限
https://ja.wikipedia.org/wiki/順序数
https://ja.wikipedia.org/wiki/極限順序数
https://ja.wikipedia.org/wiki/濃度 (数学)
https://ja.wikipedia.org/wiki/アレフ数
https://ja.wikipedia.org/wiki/連続体仮説
https://ja.wikipedia.org/wiki/選択公理
https://ja.wikipedia.org/wiki/構成主義 (数学)
https://ja.wikipedia.org/wiki/ミレニアム懸賞問題
https://ja.wikipedia.org/wiki/シミュレーション仮説
参考URL
ニコニコ大百科 圏論
https://dic.nicovideo.jp/a/圏論
世界の言語の数体系
http://www.sf.airnet.ne.jp/~ts/language/numberj.html
計算可能な実数と定義可能な実数1
https://ameblo.jp/darainao/entry-10785064499.html
書籍
数は科学の言葉 2016/6/8 トビアス ダンツィク、Number: The Language of Science
数学 その形式と機能 1992/4/1 S. マックレーン、Mathematics, Form and Function
〈現実〉とは何か 2019/12/13 西郷甲矢人, 田口茂
もっとも美しい対称性 2008/10/16 イアン・スチュアート
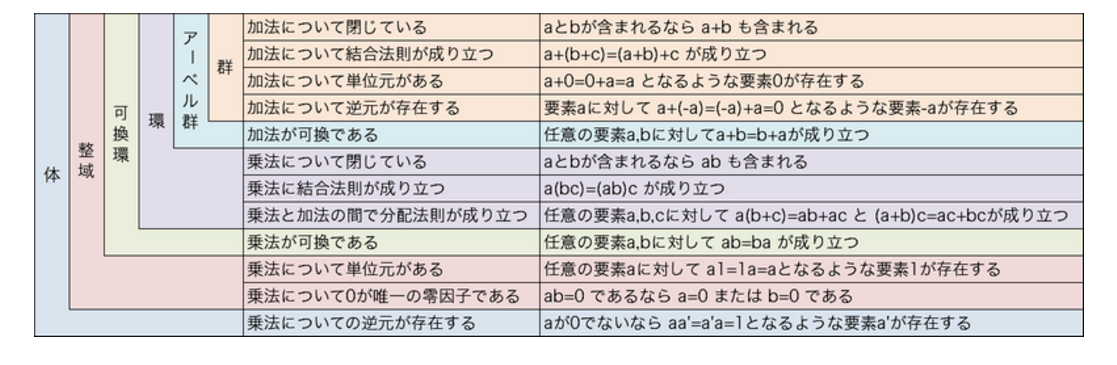
付録1 群、環、体
大人になってからの再学習より http://zellij.hatenablog.com/entry/20121211/p1