はじめに
本記事は2024/2/3(土)秋葉原ロボット部 「理論グーループ勉強会」 14:00〜17:00 にて、話した内容をまとめたものです。
理論グループ 勉強会 https://akbrobot.connpass.com/event/307848/
「座標系をローレンツ変換してみた」 使用したつぎのPythonライブラリは良さそう。
・numpy.einsum: アインシュタインの縮約記法
・SymPy: 数式処理システム
ローレンツ変換の参考本「一般相対性理論を一歩一歩数式で理解する」 P320、P324
本記事のポイント
- デバッグ出力が数式表現 「$\beta = V/c$」で見やすい。(sympy.display, sympy.Eq, sympy.subs)
- はじめは数式世界で、途中から数値世界へ移行する。(sympy.evalf または sympy.N)
- Python プログラム行数が短い、グラフ生成を含めて40行。
アインシュタイン縮約記法(numpy.einsum)により多重ループが1行で書ける。走る添字数分のループを書かなくてよい。
デバッグ出力 (sympy.display、ローレンツ変換行列)
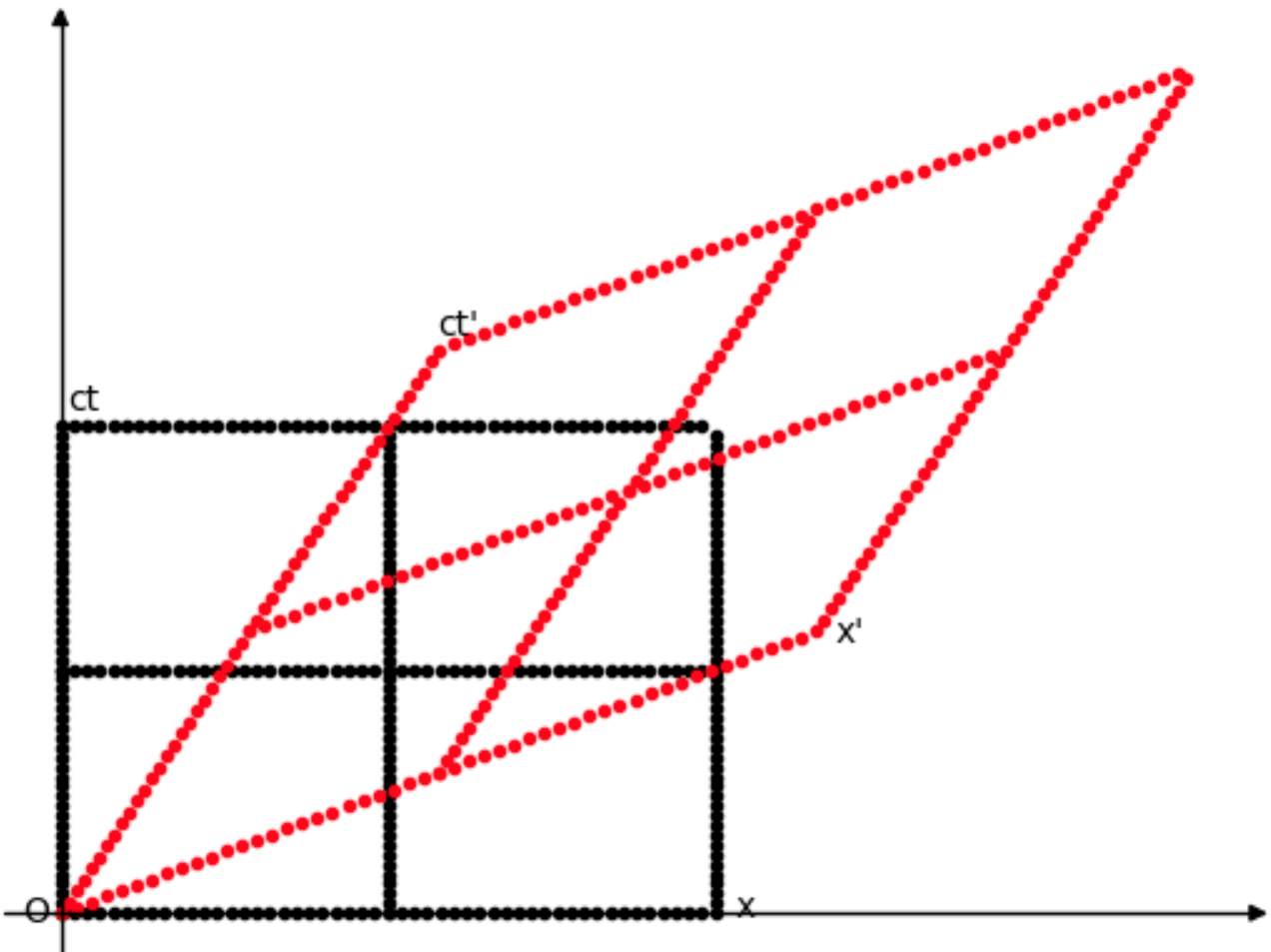
グラフ出力 (1/2光速、基底ベクトルのローレンツ変換)
Python プログラム (SymPy、numpy.einsum)
import numpy as np
import sympy
import matplotlib.pyplot as plt
from mpl_toolkits.axisartist.axislines import AxesZero
X = Y = np.arange(0, 1, 0.02)
sympy.var('V,c,beta,gamma,Lambda,e')
l = sympy.Matrix([[gamma, -gamma*beta],[-gamma*beta, gamma]])
b = sympy.Eq(beta,V/c)
g= sympy.Eq(gamma,1/sympy.sqrt(1-(V**2/c**2)))
display("Lambda=",l,g,b)
l = l.subs([(b.lhs, b.rhs), (g.lhs, g.rhs)]); display("Lambda=",l)
l0 = np.array(l.subs(V, 0).evalf(3), dtype='float64'); display("V=0",l0)
l1 = np.array(l.subs(V, c/2).evalf(3), dtype='float64'); display("V=c/2",l1)
l1inv= np.linalg.inv(l1); display("inv",l1inv) # basis vector transformation
fig = plt.figure()
ax = fig.add_subplot(1,1,1,axes_class=AxesZero)
for direction in ["xzero", "yzero"]:ax.axis[direction].set_axisline_style("-|>");ax.axis[direction].set_visible(True)
for direction in ["left", "right", "bottom", "top"]: ax.axis[direction].set_visible(False)
ax.text(-0.06, -0.02, "O")
ax.axes.xaxis.set_ticks([]);ax.axes.yaxis.set_ticks([])
# ax.autoscale(enable=False)
for color in ['black', 'red']:
if color == 'black':
A = l0
mark="x","ct"
else:
A = l1inv
mark="x'","ct'"
x = y = np.array([0] *X.shape[0])
for i in range(Axis:=3):
Xy = np.array([X,y]) # x axis
XyP = np.einsum("ij,jk->ik",A,Xy)
plt.plot(XyP[0], XyP[1], ".",color=color)
if i==0 :plt.text(0.05+(XyP[0])[X.shape[0]-1], -0.01+ (XyP[1])[X.shape[0]-1], mark[0])
xY = np.array([x,Y]) # ct axis
xYP = np.einsum("ij,jk->ik",A,xY)
plt.plot(xYP[0], xYP[1], ".",color=color)
if i==0 :plt.text(0.01+(xYP[0])[X.shape[0]-1], 0.05+ (xYP[1])[X.shape[0]-1], mark[1])
x = y = x+(1/(Axis-1))
おわりに
つぎの2つのPythonライブラリは、使えそう。
・numpy.einsum: アインシュタインの縮約記法
・SymPy: 数式処理システム
数式レベルでのデバッグ出力は楽しい。行列を含んだ等式(sympy.Eq)は使用できない?
einsum は強力でプログラムを短くできる。
相対論や量子論の分野のPythonライブラリが多数ある。機会を見つけて使用したい。
参考資料
一般相対性理論を一歩一歩数式で理解する 2017 石井俊全
アインシュタインの縮約記法ってナンだ?
https://qiita.com/tshimizu8/items/a56795bdc34aaeaa2594
https://docs.sympy.org/dev/tutorials/intro-tutorial/intro.html#what-is-symbolic-computation
参考 Wikipedia
https://ja.wikipedia.org/wiki/SymPy
https://ja.wikipedia.org/wiki/数式処理システム
https://ja.wikipedia.org/wiki/ローレンツ変換
付録
使用環境
- Google Colaboratory
!python -V
! pip list | grep -E "numpy"
! pip list | grep -E "sympy"
! pip list | grep -E "matplot"
!cat /etc/os-release | head -n 2 | tr "\n" " "; echo
!uname -a
# !nvidia-smi
# !cat /proc/cpuinfo
# !cat /proc/meminfo
Python 3.10.12
numpy 1.23.5
sympy 1.12
matplotlib 3.7.1
matplotlib-inline 0.1.6
matplotlib-venn 0.11.10
PRETTY_NAME="Ubuntu 22.04.3 LTS" NAME="Ubuntu"
Linux e96af331b621 6.1.58+ #1 SMP PREEMPT_DYNAMIC Sat Nov 18 15:31:17 UTC 2023 x86_64 x86_64 x86_64 GNU/Linux
相対論と量子論のPythonライブラリ情報(ChatGPT)
相対論
- EinsteinPy: 一般相対性理論と宇宙物理学のためのPythonライブラリ、軌道計算や時空の可視化が可能。
- NRPy+ (Numerical Relativity in Python): 数値相対論のためのPythonパッケージ、一般相対性理論の方程式から数値コードを自動生成。
- PyCBC: 重力波信号の解析と検出に特化したPythonライブラリ、LIGOやVirgoのデータ処理に使用。
量子論
- QuTiP (Quantum Toolbox in Python): 量子力学と量子情報学のためのツールボックス、量子システムのダイナミクスシミュレーションをサポート。
- QuantumPy: 量子力学のシミュレーションに特化したPythonライブラリ、基本的な量子計算を行うための関数を提供。
- Qutip-qip: QuTiPの一部であり、量子情報処理の実験をシミュレートするためのモジュール。
量子化学
- Psi4: 高度な量子化学計算を行うためのオープンソースソフトウェアパッケージです。エネルギー計算、勾配計算、その他多くの量子化学的特性の計算をサポートしています。
- PySCF: 軽量で柔軟性が高く、拡張しやすい量子化学計算のためのPythonライブラリです。密度汎関数理論(DFT)、結合クラスター理論など多岐にわたる方法をサポートしています。
- RDKit: 化学情報学および機械学習アプリケーション向けのオープンソースのツールキットです。分子の生成、操作、分析、可視化などが可能で、量子化学計算と組み合わせて使用されることがあります。