前回までのあらすじ

前回の記事でどこでもドアのワープを実装したら、そこには映ってはイケないものが。。。

白いやつ、あんたは映っちゃだめなんですよ。

今回やること

ということで今回はこのどこでもドアに後ろにあって、映るべきでない白いやつを映らないようにしたいと思います。

実装までの道のり

結論を知りたい人は記事下部の「スクリプトの実装とカメラへの設定」へどうぞ

Oblique Near-Plane Clipping

ここで登場するのが Oblique Near-Plane Clipping というテクニック。
(詳しい解説は後日補足編を記事にします)

大層な名前がついていますが、簡単に言うとカメラのクリップ(Clipping)空間の近接面(Near-Plane)を斜め(Oblique)にしたものを設定するテクニックです。
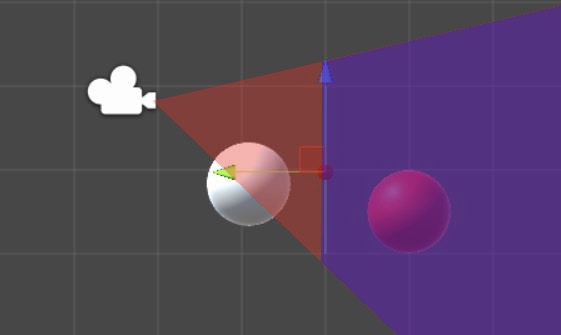
もっと早い話が以下の青い空間にあるオブジェクトだけ、描画対象にするためのテクニックです。

どうやるのか？
残念ながらエディタのどこを見てもそんな事ができる設定はなさそう。。。
いろいろ探した結果 Camera.CalculateObliqueMatrix なるメソッドを発見！

clipPlaneを表すVector4を渡すと、それをNear-PlaneとするProjection Matrixを返してくれるらしい。

Camera.CalculateObliqueMatrixってどうやって使うの？

というかそもそもこのclipPlaneってなんだ？？？
メソッド公開するならもうちょっとドキュメント書いてくれよ。。。と愚痴を述べつつ
色々調べた結果以下の式の $ (a, b, c, d) $ をVector4として渡すようです。

ax + by + cz + d = 0

さて、ここで高校数学が登場します(まじかよ。。。

平面の方程式の求め方

3次元空間における平面の方程式は、以下の2つの要素があれば求めることが出来ます。

正規化された平面の単位法線ベクトル $ \vec{n} $
平面上の任意の点 $ p $

詳しい解説は検索してもらえればと思います。
答えは $ a, b, c $ は $ \vec{n} $ の各要素、$ d $ は $ -\vec{n} \cdot p $ になります。

平面を求めるメソッドのコーディング

上記の法則に従いCalculateClipPlaneメソッドを実装します。

static Vector4 CalculateClipPlane(Vector3 clip_plane_normal, Vector3 clip_plane_arbitary_position) {
  float distance = -Vector3.Dot(clip_plane_normal, clip_plane_arbitary_position);
  Vector4 clip_plane = new Vector4(clip_plane_normal.x, clip_plane_normal.y, clip_plane_normal.z, distance);

  return clip_plane;
}

上記のメソッドに平面の単位法線ベクトル、平面上の任意の点を渡せば平面の方程式がVector4で取得できます。

平面と垂直な法線と平面上の任意の点

これはちょうどいいものが有ります。Near-Clip PlaneとしてTransformを使いましょう。
transform.forward(zの正の向き)を法線、transfrom.positionを平面上の任意の点としましょう。
xy-平面をそのまま平面として扱うイメージです。

よし、これで解決！！！　になりません。。。

カメラ空間のパラメータを求める

実はCamera.CalculateObliqueMatrixに渡すパラメータはカメラ空間で渡す必要があるようです。
(この部分も補足編に少し書こうと思います。)

ということでCalculateClipPlaneに渡すパラメータもカメラ空間に変換しましょう。
Camera.worldToCameraMatrixでカメラ空間に変換するmatrixが取得出来ます。
これを使うことでカメラ空間における平面に垂直な法線と平面上の任意の点が求められます。

Matrix4x4 world_to_camera_matrix = camera.worldToCameraMatrix;
Vector3 clip_plane_normal = world_to_camera_matrix.MultiplyVector(clip_plane_transform.forward);
Vector3 clip_plane_arbitary_position = world_to_camera_matrix.MultiplyPoint(clip_plane_transform.position);

後はこれをCalculateClipPlaneに渡せばカメラ空間での平面の方程式がVector4で求められます。

スクリプトの実装とカメラへの設定

ここまでくれば後はUnity向けに実装するだけです。
※カメラ空間におけるClip Planeの位置は、カメラが移動すると変わることに注意してください。

以下はサンプルなのでよろしければ参考にして下さい。

using UnityEngine;

[RequireComponent(typeof(Camera))]
public class NearPlaneClip : MonoBehaviour {
  private Camera _camera;

  // Near-Clip Planeとして扱うTransform
  public Transform _clip_plane;

  void Start() {
    // Cameraコンポーネントを取り出す
    _camera = GetComponent<Camera>();
  }

  void LateUpdate() {
    // 毎フレーム Projection Matrix を更新
    Vector4 clip_plane = CalculateClipPlane(_camera, _clip_plane);
    _camera.projectionMatrix = _camera.CalculateObliqueMatrix(clip_plane);
  }

  private static Vector4 CalculateClipPlane(Camera camera, Transform clip_plane_transform) {
    Matrix4x4 world_to_camera_matrix = camera.worldToCameraMatrix;
    Vector3 clip_plane_normal = world_to_camera_matrix.MultiplyVector(clip_plane_transform.forward);
    Vector3 clip_plane_arbitary_position = world_to_camera_matrix.MultiplyPoint(clip_plane_transform.position);

    return CalculateClipPlane(clip_plane_normal, clip_plane_arbitary_position);
  }

  private static Vector4 CalculateClipPlane(Vector3 clip_plane_normal, Vector3 clip_plane_arbitary_position) {
    float distance = -Vector3.Dot(clip_plane_normal, clip_plane_arbitary_position);
    Vector4 clip_plane = new Vector4(clip_plane_normal.x, clip_plane_normal.y, clip_plane_normal.z, distance);

    return clip_plane;
  }
}

手順は前回の記事からの続きとして書きます。

赤カメラにアサイン
どこでもドアの移動先を想定した場所にNear-Clip Planeとして利用するTransformを設置
上記TransformをスクリプトのClip_planeに設定

これで再生すれば白球が消えると思います！

そして、いざVRへ！！！

ぼくはVRがやりたいんだ！！！
ということで、いざVRへ！
ってあれ。。。

なぜ貴様がそこにいる！？

次回に続く

今回のまとめ

今回は予告どおりストーリ調にしてみました(といっても余計なコメント追加してただけのような。。。)
まだまだどこでもドアまでの道のりは長いですが、一つずつ解決していきたいです。

よろしければ記事について、感想や指摘などお願いします。

UnityでVR対応のどこでもドア実現を目指す その２ Oblique Near-Plane Clipping編