NumPyの特徴
- 多次元配列をいっぺんに高速に計算する。
ndarray : 多次元配列オブジェクト
- ndarrayの例
import numpy as np
data = np.random.randn(2,3) # 縦2列、横3行の乱数
print(data)
# [[-0.4440664 -0.07889544 -0.84781375]
# [ 0.59333292 -0.03008522 1.54106015]]
print(data * 10) # 乗算
# [[-4.44066398 -0.78895438 -8.47813747]
# [ 5.93332925 -0.3008522 15.41060155]]
print(data + data) # 加算
# [[-0.8881328 -0.15779088 -1.69562749]
# [ 1.18666585 -0.06017044 3.08212031]]
print(data.shape) # 縦、横の要素数
# (2, 3)
print(data.dtype) # 要素の型
# float64
ndarrayの生成
-
np.array(リスト)で生成する。 -
np.zeros(10)np.zeros((3,6))で全ての要素が0のndarrayを生成。 - 同様に、
np.ones()で全ての要素が1のndarrayを生成 -
np.full()は、指定された値で埋める。 -
np.arange(10)で、0〜9の要素が順に入ったndarrayを生成。
import numpy as np
data = [[1, 2, 3, 4], [5, 6, 7, 8]]
arr = np.array(data) # リストからndarrayを生成
print(arr)
# [[1 2 3 4]
# [5 6 7 8]]
print(arr.ndim) # 次元
# 2
print(arr.shape) # 要素数
# (2, 4)
ndarrayのデータ型
- int8、16、32、64、uint8、16、32、64
- float16、32、64、128
- complex64、128、256
- bool
- object
- string_
- unicode_
import numpy as np
arr1 = np.array([-3.7, -1.2, 0.5, 4.5])
print(arr1)
# [-3.7 -1.2 0.5 4.5]
arr2 = arr1.astype(np.int32) # キャストする
print(arr2)
# [-3 -1 0 4]
arr3 = np.array(['-3.7', '-1.2', '0.5', '4.5'], dtype=np.string_)
print(arr3)
# [b'-3.7' b'-1.2' b'0.5' b'4.5']
print(arr3.dtype)
# |S4
arr4 = arr3.astype(np.float64) # キャストする
print(arr4)
# [-3.7 -1.2 0.5 4.5]
ndarrayの算術演算
- 同じサイズ同士の演算は、同位置同士で計算される。
- サイズの異なるndarray同士の演算は、ブロードキャストと呼ばれる。
import numpy as np
arr1 = np.array([[1., 2., 3., 4.], [5., 6., 7., 8.]])
print(arr1 ** 2)
# [[ 1. 4. 9. 16.]
# [25. 36. 49. 64.]]
print(arr1 - arr1)
# [[0. 0. 0. 0.]
# [0. 0. 0. 0.]]
print(1 / arr1)
# [[1. 0.5 0.33333333 0.25 ]
# [0.2 0.16666667 0.14285714 0.125 ]]
arr2 = np.array([[0., 4., 1., 5.], [3., 9., 4., 9.]])
print(arr1 < arr2)
# [[False True False True]
# [False True False True]]
インデックス参照とスライシングの基礎
- インデックス参照は、データから一部を切り出す。
- 切り出した一部に、スカラーを指定することができ、指定した値が切り出した全体に伝播する。(ブロードキャスト)
- スライスはコピーではなく、ビュー。
import numpy as np
arr1 = np.arange(10)
print(arr1)
# [0 1 2 3 4 5 6 7 8 9]
print(arr1[5:8])
# [5 6 7]
arr1[5:8] = 12
print(arr1)
# [ 0 1 2 3 4 12 12 12 8 9]
arr_slice = arr1[5:8]
arr_slice[1] = 12345
print(arr_slice)
# [ 12 12345 12]
print(arr1)
# [ 0 1 2 3 4 12 12345 12 8 9]
- 2次元のスライス
arr2d = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]]) # 2次元
print(arr2d)
# [[1 2 3]
# [4 5 6]
# [7 8 9]]
print(arr2d[:2]) # 縦の0,1番目を取り出す
# [[1 2 3]
# [4 5 6]]
print(arr2d[:2, 1:]) # 縦の0,1番目、横路の1,2番目を取り出す
# [[2 3]
# [5 6]]
print(arr2d[1, :2]) # 縦の1番目、横路の0,1番目を取り出す
# [4 5]
print(arr2d[:, :1]) # 縦全部、横路の0,1番目を取り出す
# [[1]
# [4]
# [7]]
arr2d[:2, 1:] = 0 # その範囲に全て代入する
print(arr2d)
# [[1 0 0]
# [4 0 0]
# [7 8 9]]
ブールインデックス参照
- 7個の配列をもつ配列の条件(真偽値配列)を元にして、(7,4) の二次元配列の行を取り出すことができる。
- 参照先配列の軸の要素数と、真偽値配列の要素数が一致しなければならない。
import numpy as np
names = np.array(['Yamada', 'Suzuki', 'Sato', 'Yamada', 'Tanaka', 'Tanaka', 'Sato'])
data = np.random.randn(7, 4) # 乱数で、縦7行、横4列の配列を作成
print(data)
# [[-0.92866442 -0.81744986 1.11821763 -0.55440628]
# [-0.09511771 0.99145963 0.38475434 0.59748055]
# [ 0.0444708 -0.00381292 0.97888419 1.242504 ]
# [ 0.89214068 -1.0411466 0.90850611 -2.02933442]
# [ 0.78789041 -0.84593788 -0.5624772 0.32488453]
# [ 0.50153002 -0.25411512 0.30855623 -1.31825153]
# [-0.6596584 1.53735231 -0.37044833 1.93782111]]
print(names == 'Yamada') # 'Yamada' が一致す流、0,4番目ばTrueを返す
# [ True False False True False False False]
print(data[names == 'Yamada']) # dataから0,4番目を取り出す
# [[-0.92866442 -0.81744986 1.11821763 -0.55440628]
# [ 0.89214068 -1.0411466 0.90850611 -2.02933442]]
mask = (names == 'Yamada') | (names == 'Sato') # orで取り出すこともできる
print(data[(names == 'Yamada') | (names == 'Sato')])
# [[-0.92866442 -0.81744986 1.11821763 -0.55440628]
# [ 0.0444708 -0.00381292 0.97888419 1.242504 ]
# [ 0.89214068 -1.0411466 0.90850611 -2.02933442]
# [-0.6596584 1.53735231 -0.37044833 1.93782111]]
data[names == 'Yamada'] = 0 # 0,4番目に、0を入れる
print(data)
# [[ 0. 0. 0. 0. ]
# [-0.09511771 0.99145963 0.38475434 0.59748055]
# [ 0.0444708 -0.00381292 0.97888419 1.242504 ]
# [ 0. 0. 0. 0. ]
# [ 0.78789041 -0.84593788 -0.5624772 0.32488453]
# [ 0.50153002 -0.25411512 0.30855623 -1.31825153]
# [-0.6596584 1.53735231 -0.37044833 1.93782111]]
ファンシーインデックス参照
- ファンシーインデックス参照とは、インデックス参照に整数配列を用いる方法。
- スライシングとは異なり、ファンシーインデックス参照は、常に元データのコピーを返す
import numpy as np
arr = np.arange(32).reshape(8, 4) # 8,4 の配列を作成
print(arr)
# [[ 0 1 2 3]
# [ 4 5 6 7]
# [ 8 9 10 11]
# [12 13 14 15]
# [16 17 18 19]
# [20 21 22 23]
# [24 25 26 27]
# [28 29 30 31]]
print(arr[[0, 4, 5, -1]]) # 0, 4, 5, -1行を返す
# [[ 0 1 2 3]
# [16 17 18 19]
# [20 21 22 23]
# [28 29 30 31]]
print(arr[[1, 5, 7, 2], [0, 3, 1, 2]]) # (1,0),(5,3),(7,1),(2,2) を返す
# [ 4 23 29 10]
転置行列、行と列の入れ替え
- ndarrayの転置はオリジナル行列を再構成した特別なビューを戻す。コピーは生成しない。
-
transpose関数を適用する方法と、ndarrayの属性の1つであるTを参照する方法がある。
import numpy as np
arr1 = np.arange(15).reshape(3, 5) # 3,5 の配列を作成
print(arr1)
# [[ 0 1 2 3 4]
# [ 5 6 7 8 9]
# [10 11 12 13 14]]
print(arr1.T)
# [[ 0 5 10]
# [ 1 6 11]
# [ 2 7 12]
# [ 3 8 13]
# [ 4 9 14]]
arr2 = np.arange(24).reshape((2, 3, 4)) # (2,3,4) の配列を作成
print(arr2)
# [[[ 0 1 2 3]
# [ 4 5 6 7]
# [ 8 9 10 11]]
#
# [[12 13 14 15]
# [16 17 18 19]
# [20 21 22 23]]]
print(arr2.transpose((1, 0, 2))) # 軸の順番を入れ替えて、(3,2,4)の配列にした
# [[[ 0 1 2 3]
# [12 13 14 15]]
#
# [[ 4 5 6 7]
# [16 17 18 19]]
#
# [[ 8 9 10 11]
# [20 21 22 23]]]
ユニバーサル関数:すべての配列要素への関数適用
- ユニバーサル関数は、ndarrayを対象に、要素ごとの捜査結果を戻す関数。
- 単項ufunc 1つのndarrayをとる
- abs, fabs, sqrt, square, exp, log, log10, log2, log1p, sign, cell, floor, rint modf, isnan, isfinite, isinf, cos, sin, tan など
- 二項ufunc 2つのndarrayをとる
- add, subtract, multiply, divide, floor_dvide, power, maximum, fmax, minimum, fmin, mod, copysign, grater, less, equal, logical_and など
ndarrayによる配列指向プログラミング
- 格子点状のデータに対して
sqrt(x^2 + y^2)の結果を表示する -
np.meshgridは2つの1次元関数をとり、それぞれの要素の全ての組み合わせを列挙する。
import numpy as np
import matplotlib.pyplot as plt
points = np.arange(-5, 5, 0.01) # 1000個の格子点
xs, ys = np.meshgrid(points, points) # 全ての組み合わせを返す
z = np.sqrt(xs ** 2 + ys ** 2)
print(z)
plt.imshow(z, cmap=plt.cm.gray)
plt.colorbar()
plt.title("Image plot of $\\sqrt{x^2 + x^2}$ for a grid of values")
plt.show()

条件制御のndarrayでの表現
-
np.where()は、第一引数がTrueの時第2引数、それ以外の時第3引数を返す。- それぞれの引数が、リスト値でもスカラー値でも良い。
import numpy as np
import matplotlib.pyplot as plt
xarr = np.array([1.1, 1.2, 1.3, 1.4, 1.5])
yarr = np.array([2.1, 2.2, 2.3, 2.4, 2.5])
cond = np.array([True, False, True, True, False])
# cond が True の時x、それ以外y をとる
# 内包表記(遅い)
reult1 = [(x if c else y) for x, y, c in zip(xarr, yarr, cond)]
# whereを使う
result2 = np.where(cond, xarr,yarr)
print(result2)
# [1.1 2.2 1.3 1.4 2.5]
数学関数、統計関数
axisでどの軸を中心に処理するか指定する
- arr.sum()、arr.mean() 全体の合計と平均
- arr.sum(axis=1)、arr.mean(axis=0) 2次元の時、それぞれ横列の合計と縦列の平均
真偽値配列関数
-
arrがnp.arrayの時、(arr>0).sum()は、正の数(True)の個数 -
bool=真偽値配列のとき-
bools.any()1でもTrueがあれば、True -
bools.all()全部がTrueであれば、True
-
ソート
-
arrがnp.arrayの時、arr.sort()で自分自身をソートする。(破壊的) - 多次元配列の場合、
arr.sort(1)のように、任意の軸を指定する。
集合関数:uniqueなど
-
np.unique(arr)は、重複を排除して、ソートした結果を返す。 -
np.inld(arr, [2, 3, 6])は、arrのリストに、2,3,6が含まれていればTrue、それ以外はFalseをarrと同じ長さのリストを返す。
ndarrayのファイル入出力
- テキストファイルや、テーブル形式データを読み込むのに、多くは
pandasを用いる。 - ここではバイナリフォーマットにフォーカスする。
-
arrを保存するには、np.save('some_array', arr)で無圧縮で保存する。拡張子は自動的に、.npyが付加される。 - 同様に、読み込みは、
arr = np.load('save_array.npy')で読み込む。 -
np.savez('array_archive.npz', a=arr1, b=arr2)で、複数のarrを無圧縮で保存する。a,bは、ディクショナリのキーとなる。 -
arch = np.load('array_archive.npz')で読み込む。loadzではない。-
arch['a']でarr1を取り出す。arch['b']でarr2を取り出す。
-
-
np.savez_compressed('arrays_compressed.npz', , a=arr1, b=arr2)で圧縮して保存する。読み込みは、上記と同様。
行列計算
- 内積の計算には。
dotを用いる。
import numpy as np
x = np.array([[1., 2., 3.], [4., 5., 6., ]])
y = np.array([[6., 23.], [-1., 7.], [8., 9.]])
print(x.dot(y)) # 内積
# [[ 28. 64.]
# [ 67. 181.]]
print(np.dot(x, y)) # 別の書き方
# [[ 28. 64.]
# [ 67. 181.]]
print(x @ y) # @ も使える。
# [[ 28. 64.]
# [ 67. 181.]]
擬似乱数生成
-
np.random.normal(size=(4,4))で4x4の行列に対して、normalを用いて、正規分布に基づいた乱数を生成する。 -
randint与えられた整数範囲内での整数乱数を返す。
import numpy as np
import matplotlib.pyplot as plt
samples = np.random.normal(size=(4,4))
print(samples)
# [[ 1.45907882 1.78873804 -0.52480754 0.20770224]
# [-1.55474475 -1.67045483 -1.3589208 1.25584424]
# [ 0.90562937 -1.50742692 1.48579887 1.48081589]
# [ 1.3478]5606 -0.20653648 0.13308665 -0.24455952]
例:ランダムウォーク
多重ランダムウォーク
- ランダムウォークで、5000回試行のもと、最初に30か-30に到達したインデックスをいっぺんに求める
import numpy as np
import matplotlib.pyplot as plt
nwalks = 5000
nsteps = 1000
# 0か1をランダムに生成
draws = np.random.randint(0, 2, size=(nwalks, nsteps))
print(draws)
# [[1 1 1 ... 0 1 1]
# [1 1 0 ... 0 0 1]
# [0 0 1 ... 1 1 0]
# ...
# [0 0 1 ... 0 0 0]
# [0 0 1 ... 1 0 0]
# [1 0 1 ... 1 1 0]]
# 0 と 1 を -1 と 1 に分ける
steps = np.where(draws > 0, 1, -1)
print(steps)
# [[ 1 1 1 ... -1 1 1]
# [ 1 1 -1 ... -1 -1 1]
# [-1 -1 1 ... 1 1 -1]
# ...
# [-1 -1 1 ... -1 -1 -1]
# [-1 -1 1 ... 1 -1 -1]
# [ 1 -1 1 ... 1 1 -1]]
# 横方向に加算していく
walks = steps.cumsum(1)
print(walks)
# [[ 1 2 3 ... 10 11 12]
# [ 1 2 1 ... -44 -45 -44]
# [ -1 -2 -1 ... -28 -27 -28]
# ...
# [ -1 -2 -1 ... 6 5 4]
# [ -1 -2 -1 ... -6 -7 -8]
# [ 1 0 1 ... 28 29 28]]
print(walks.max())
# 128
print(walks.min())
# -123
# 30に到達したか? 横列単位で True / False で返す
hits30 = (np.abs(walks) >= 30).any(1)
print(hits30)
# [False False True ... True True True]
# 30 か -30 に到達した数
print(hits30.sum())
# 3377
# 30/-30に到達した行を取り出し、一番最初のインデックスを求める
crossing_times = (np.abs(walks[hits30]) >= 30).argmax(1)
print(crossing_times)
# [671 313 161 ... 307 289 89]
# 平均
print(crossing_times.mean())
# 500.09327805744744
# グラフに表示する
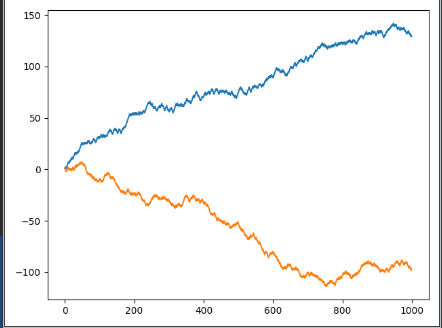
max_row = walks[(walks == walks.max()).any(1)][0]
min_row = walks[(walks == walks.min()).any(1)][0]
plt.plot(max_row)
plt.plot(min_row)
plt.show()
- ランダムウォークの最大と最小のグラフ
参考
- Pythonによるデータ分析入門 第2版