はじめに
機械学習のToyデータであるカルフォルニア住宅価格のデータセットで因果探索にトライ
また、分析しやすくするために以下のLiNGAMのライブラリの便利な機能を利用します
| 項目 | 内容 |
|---|---|
| 因果グラフの表示簡略化 | 因子数が多いと表示される因果グラフが複雑になり解釈が困難なため、パス係数で表示する因果パスを絞る |
| 事前知識の導入 | 予め因果の有無/方向が分かっている場合は、条件として与えて因果探索させる |
| 信頼性評価 | 信頼性の高い因果パスに絞り分析できるようにする |
LiNGAMとは
前回のこちらの記事を参照してください。
LiNGAMの利用には以下の前提を満たす必要があります。
- 因果関係は線形
- 誤差分布が非ガウス分布に従う
- 因果グラフは非循環で表現できる
- 未観測の要因が存在しない
現実の問題に適用するには非常に厳しい条件で、
今回のカルフォルニアの住宅価格のデータセットに対して適切かという問題がありますが。。
カルフォルニア住宅価格のデータセットとは
- 1990年の米国国勢調査から得られたカリフォルニア州の住宅価格
- データ数は20640件。住宅価格(地域の中央値)以外に地域の築年数中央値や人口など8種類のデータを含む
- 住宅価格を予測するタスクとして、機械学習のToyデータとして利用される
- scikit-learnのライブラリからも取得可能
- 詳細は以下のページを参照
https://atmarkit.itmedia.co.jp/ait/articles/2201/31/news042.html
LiNGAMによる因果グラフ推論
データの準備
影響の大きさを比較しやすくするためカラム毎に正規化処理。
from sklearn.datasets import fetch_california_housing
import numpy as np
import pandas as pd
#住宅価格データセットの読み込み
data_housing = fetch_california_housing()
df = pd.DataFrame(data_housing.data, columns=data_housing.feature_names).assign(Target=np.array(data_housing.target))
#正規化
df=df.apply(lambda x: (x-x.mean())/x.std(), axis=0)
#日本語のラベル名を準備
label_detail=['所得','築年数','総部屋数','総寝室数','人口','総世帯数','緯度','経度','住宅価格']
因果探索
ライブラリを利用
公式ドキュメント:https://lingam.readthedocs.io/en/latest/index.html
import graphviz
import lingam
from lingam.utils import make_dot,print_causal_directions, print_dagc,make_prior_knowledge
# numpyでの小数点以下桁数表示と指数表記の禁止を設定
np.set_printoptions(precision=3, suppress=True)
# 再現性のためにランダムシードを固定
np.random.seed(0)
#因果探索実行
model = lingam.DirectLiNGAM()
model.fit(df)
#因果グラフ出力
make_dot(model._adjacency_matrix,labels=label_detail)
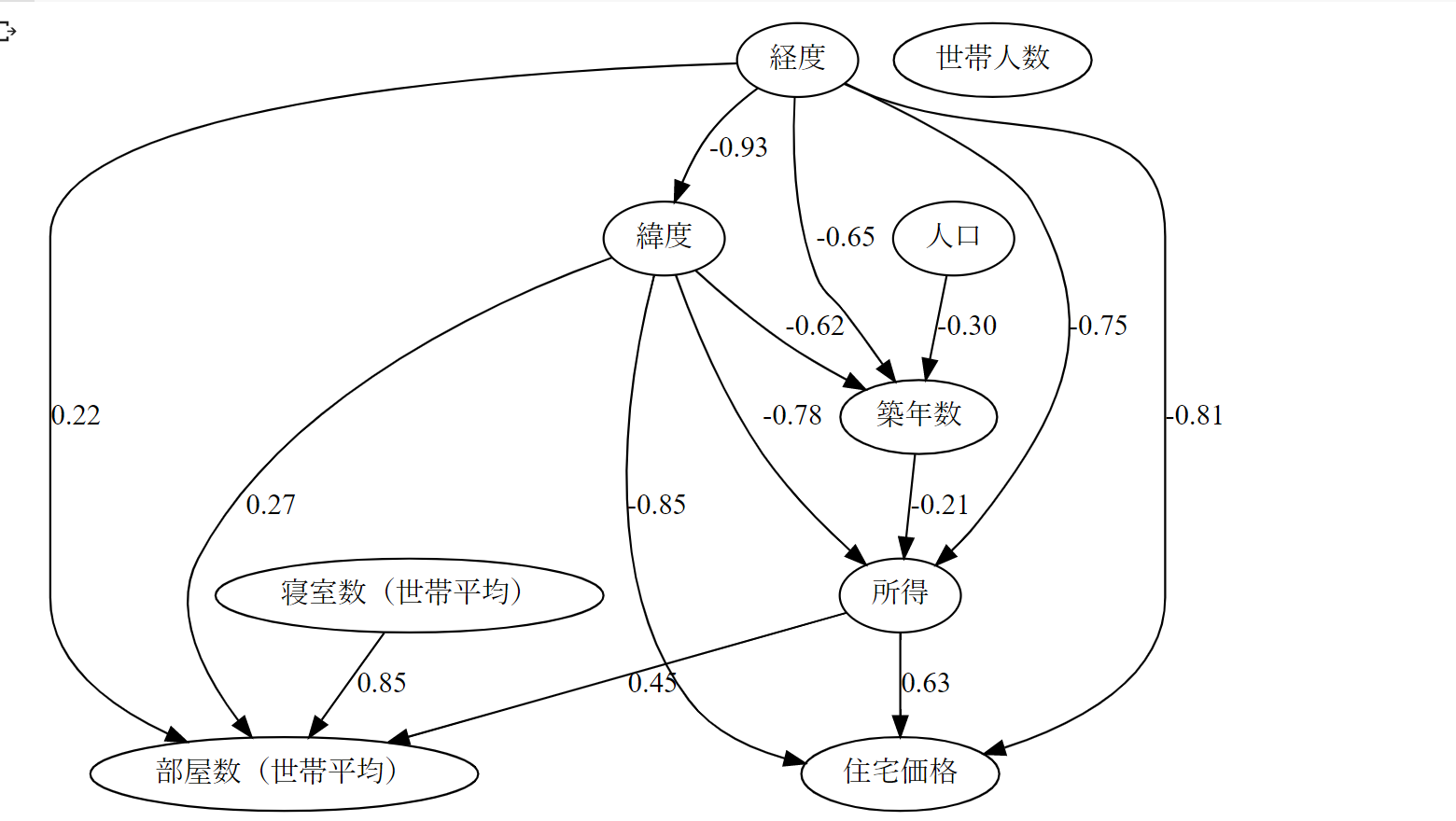
結果
以下の通り。かなりカオス。
このグラフから結果を解釈するのは骨が折れそう。。
表示する因果パスを絞る
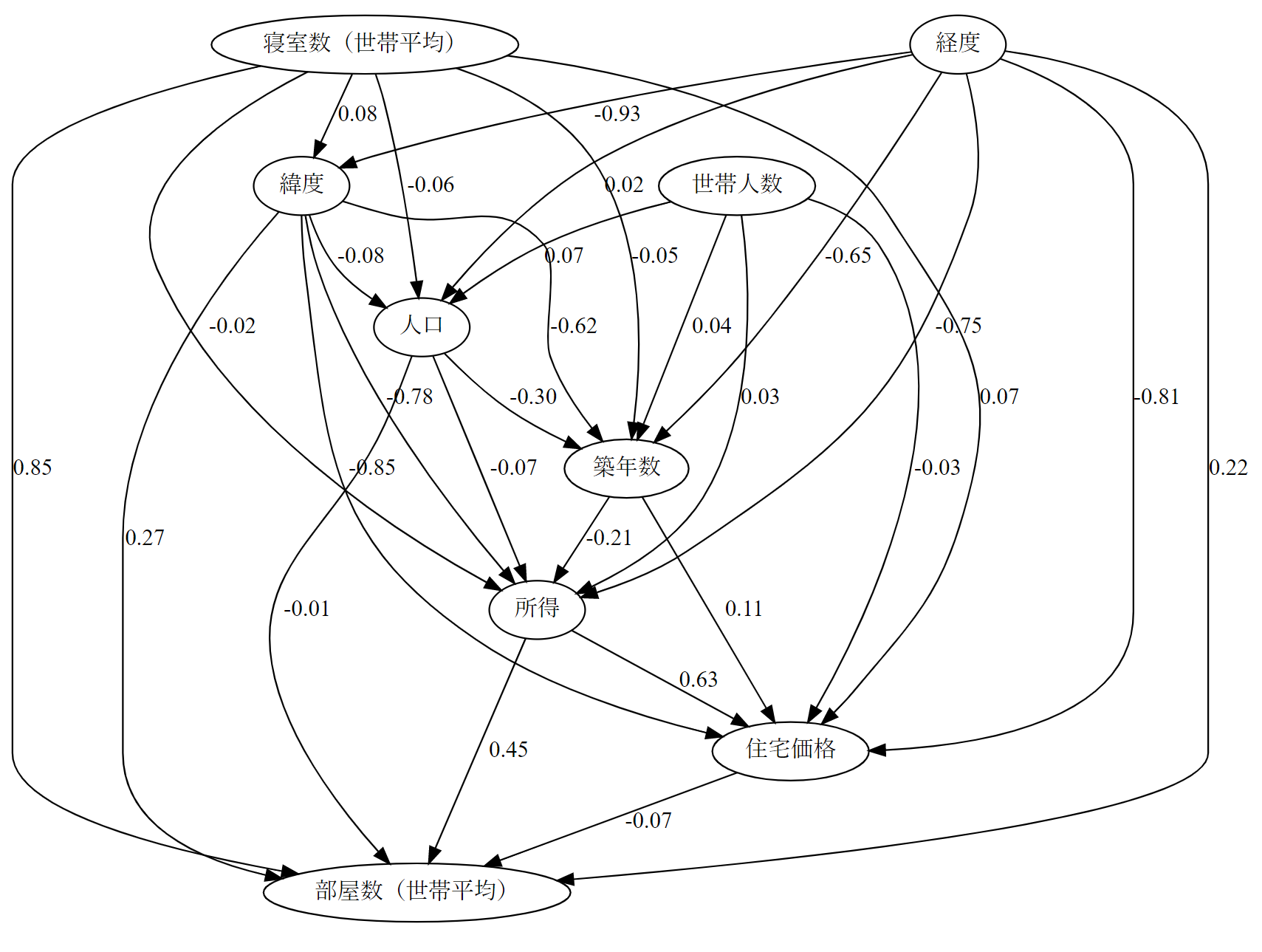
見やすくするために係数の絶対値が小さいパスを除くようlower_limitを指定します。今回は0.2にしました。
make_dot(model._adjacency_matrix,labels=label_detail,lower_limit=0.2)
結果は以下の図の通り。
- 所得が高いと住宅価格も高い(妥当そう)
- 所得が高いと部屋数も多い(妥当そう)
- 寝室数が多いと部屋数も多い(妥当そう)
- 築年数が低いと所得が高い(築年数から住宅価格に直接、係数の高い因果パスがあると思いきや)
- 人口が多いと築年数が低い(??)
- 緯度が高いと住宅価格は低い(地域事情を知らず妥当か判断できず)
部屋数から住宅価格へ高い係数の因果パスがあるかと思いきやそうではありませんでした。
因果の解釈が難しいところもありますが、おおむね妥当そうです。
事前知識の導入
予め因果に関する知識がある場合にはモデルに与えることで反映することができます。
公式ドキュメント:https://lingam.readthedocs.io/en/latest/tutorial/pk_direct.html#how-to-use-prior-knowledge-in-directlingam
今回は「価格住宅」が他の因子に影響を与える因果パスはないとします。
ちなみにこの設定は独立主成分分析を用いたICALiNGAMでは使えません。DirectLiNGAMで使える理由として因果パスを順番に固定していく手法のため、事前知識で与えられた場合には最初にその因果パスを固定してしまえばよいためだと思います。
因果の事前知識は以下のように行列で与える必要があります。
ここで要素(i,j)はx_iからx_jへの因果を指します
| 要素の値 | 因果の存在 |
|---|---|
| 0 | 存在しない |
| 1 | 存在する |
| -1 | (事前知識なし) |
[[-1 0 -1 -1 0 -1]
[ 0 -1 -1 -1 0 -1]
[ 0 0 -1 -1 0 -1]
[ 0 0 -1 -1 0 -1]
[ 0 0 -1 -1 -1 -1]
[ 0 0 -1 -1 0 -1]]
make_prior_knowledge関数を使うと行列を簡単に生成できます。
以下では9個ある因子のうち、インデックス番号8の要素(=住宅価格)が他の因子に影響を与えることはない事前情報の行列をprior_knowledgeに格納しています。
prior_knowledge = make_prior_knowledge(
n_variables=9,
sink_variables=[8],
)
事前知識の設定はモデル宣言時にします。
model = lingam.DirectLiNGAM(prior_knowledge=prior_knowledge)
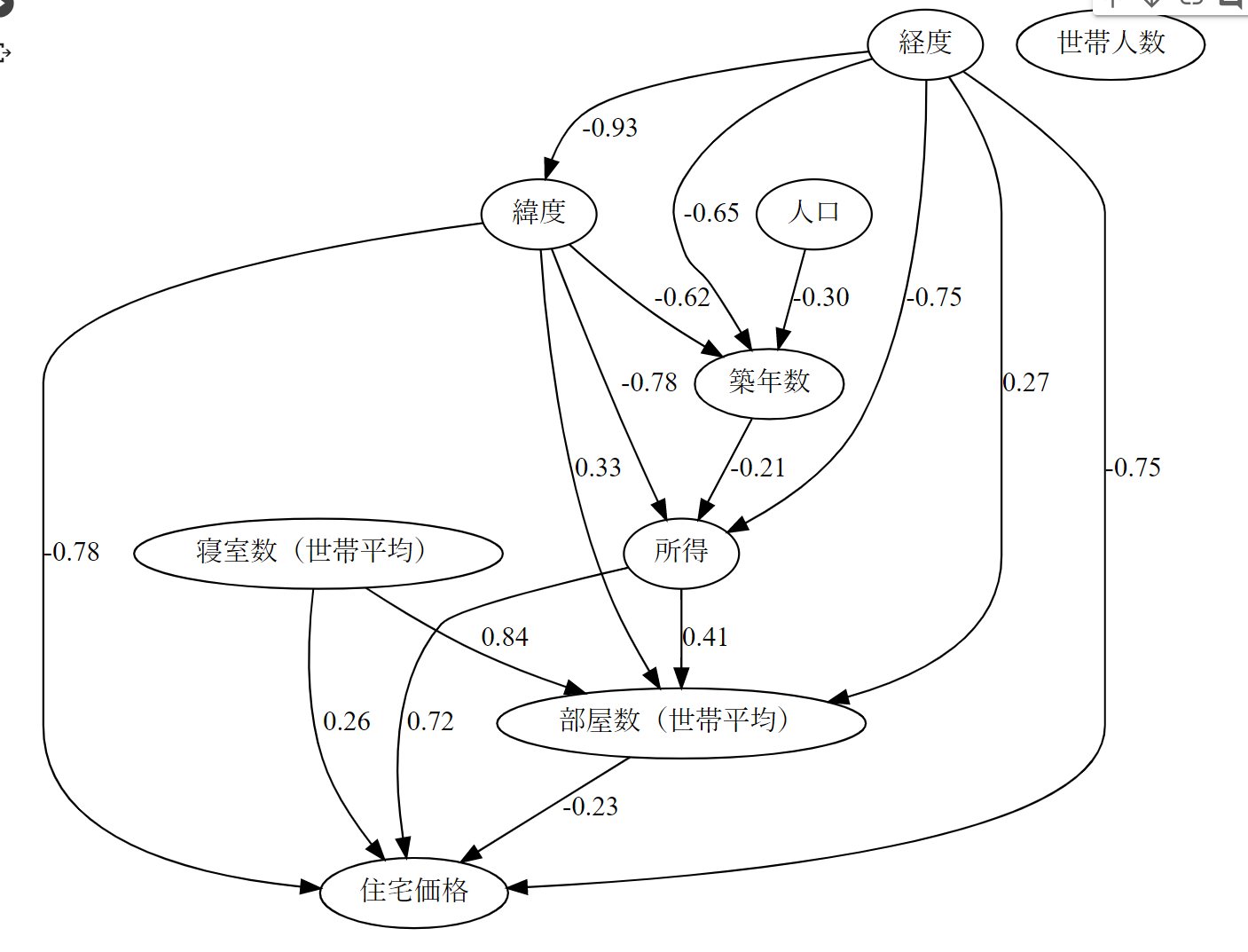
結果は以下の通りです(見やすくするためパス係数の絶対値が0.2以下のパスは除いて表示しています)
事前知識の導入した結果、「住宅価格」からは因果パスが出ておらず、一番下流になっています。
事前知識の導入しない場合と比べ、係数が変化していますが、大きく因果グラフは変化していないようです。
また「寝室数」と「部屋数」が「住宅価格」へ直接強い因果パスが現れています。
ただ意外なのが部屋数が多いと住宅価格は下がる結果になっています。
推測した因果パスの信頼性評価
以前以下の記事で紹介したブートストラップによる信頼性評価をおこないます。
パス係数により足切りすることで分析しやすくなりましたが、信頼性の観点から検討すべき因果パスを絞ることができます。
#ブートストラップ実行
result = model.bootstrap(x, n_sampling=100)
#結果の表示
causal_effects = result.get_total_causal_effects(min_causal_effect=0.01)
df = pd.DataFrame(causal_effects)
df['from'] = df['from'].apply(lambda x : label_detail[x])
df['to'] = df['to'].apply(lambda x : label_detail[x])
#効果の降順でソート
df=df.sort_values('effect', ascending=False)
df
結果は以下の通り。係数が0.01以上の因果パスは45個あり、その中でも信頼度(表でのprobality)が高い0.9以上の19個に絞ることで分析しやすくなりそうです。
| index | from | to | effect | probability |
|---|---|---|---|---|
| 0 | 経度 | 住宅価格 | -0.048 | 1.0 |
| 1 | 経度 | 人口 | 0.099 | 1.0 |
| 2 | 緯度 | 部屋数(世帯平均) | 0.088 | 1.0 |
| 3 | 寝室数(世帯平均) | 緯度 | 0.075 | 1.0 |
| 4 | 寝室数(世帯平均) | 部屋数(世帯平均) | 0.855 | 1.0 |
| 5 | 所得 | 部屋数(世帯平均) | 0.407 | 1.0 |
| 6 | 経度 | 築年数 | -0.109 | 1.0 |
| 7 | 緯度 | 住宅価格 | -1.322 | 1.0 |
| 8 | 経度 | 緯度 | -0.924 | 1.0 |
| 9 | 緯度 | 築年数 | -0.603 | 1.0 |
| 10 | 寝室数(世帯平均) | 築年数 | -0.088 | 1.0 |
| 11 | 所得 | 住宅価格 | 0.624 | 1.0 |
| 12 | 部屋数(世帯平均) | 住宅価格 | -0.238 | 1.0 |
| 13 | 人口 | 住宅価格 | -0.037 | 1.0 |
| 14 | 人口 | 築年数 | -0.3 | 1.0 |
| 15 | 寝室数(世帯平均) | 人口 | -0.07 | 1.0 |
| 16 | 築年数 | 住宅価格 | -0.026 | 0.99 |
| 17 | 緯度 | 人口 | -0.083 | 0.97 |
| 18 | 築年数 | 部屋数(世帯平均) | -0.101 | 0.95 |
| 19 | 寝室数(世帯平均) | 住宅価格 | -0.049 | 0.92 |
| 20 | 緯度 | 所得 | -0.639 | 0.88 |
| 21 | 寝室数(世帯平均) | 所得 | -0.066 | 0.88 |
| 22 | 経度 | 部屋数(世帯平均) | -0.029 | 0.87 |
| 23 | 世帯人数 | 人口 | 0.069 | 0.79 |
| 24 | 築年数 | 所得 | -0.214 | 0.77 |
| 25 | 世帯人数 | 住宅価格 | -0.033 | 0.73 |
| 26 | 人口 | 部屋数(世帯平均) | -0.011 | 0.53 |
| 27 | 世帯人数 | 所得 | 0.023 | 0.23 |
| 28 | 所得 | 築年数 | -0.129 | 0.23 |
| 29 | 人口 | 世帯人数 | 0.025 | 0.21 |
| 30 | 人口 | 所得 | -0.009 | 0.16 |
| 31 | 築年数 | 世帯人数 | 0.013 | 0.13 |
| 32 | 経度 | 世帯人数 | 0.011 | 0.13 |
| 33 | 所得 | 寝室数(世帯平均) | -0.064 | 0.12 |
| 34 | 部屋数(世帯平均) | 世帯人数 | 0.032 | 0.12 |
| 35 | 所得 | 緯度 | -0.076 | 0.12 |
| 36 | 経度 | 所得 | -0.026 | 0.12 |
| 37 | 経度 | 寝室数(世帯平均) | 0.023 | 0.05 |
| 38 | 世帯人数 | 築年数 | 0.021 | 0.05 |
| 39 | 所得 | 経度 | -0.025 | 0.05 |
| 40 | 部屋数(世帯平均) | 築年数 | -0.098 | 0.05 |
| 41 | 部屋数(世帯平均) | 人口 | -0.081 | 0.05 |
| 42 | 寝室数(世帯平均) | 経度 | 0.023 | 0.04 |
| 43 | 所得 | 人口 | -0.016 | 0.03 |
| 44 | 緯度 | 世帯人数 | -0.006 | 0.02 |
| 45 | 人口 | 緯度 | -0.01 | 0.01 |
最後に
データドリブンで因果の方向まで推測でき非常に面白い分野だと思います。
今は制約が多く適用にも課題がありますが、克服するために研究もされているようで、今後が楽しみな分野です。
余談ですがボストン住宅価格のデータはポリティカルな問題があるようですね。
はじめはボストンのデータを使っていましたが、記事をあたりカルフォルニアに切り替えて分析しなおしました。