1. 今回の目的
これまで1、2では日経平均の日足データから、翌営業日の日経平均が始値から終値にかけて上昇するか下落するか予想するプログラムを作り、簡単な交差検定で検証を行いました。いずれも予想される利益は0近辺で、利益を出すのは難しそうでした。そこで3ではニューヨーク証券取引所のNYSE総合 (NYA)の日足データも加えて予測の改善を試みました。
3では利益を期待できそうな結果になったので、今回はパラメーターを調整して性能を改善できないか試みることにします。
2. n_estimatorsの影響
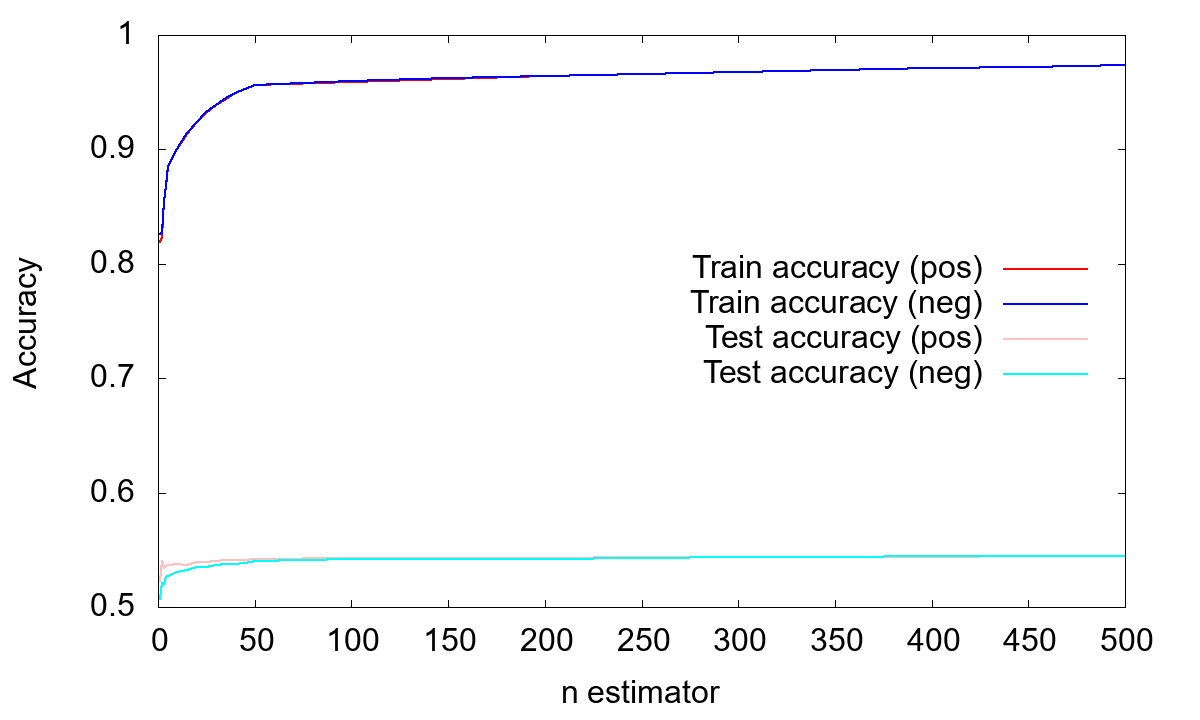
まずは__RandomForestClassifier__の__n_estimators__の影響を見てみましょう。下図は__n_estimators__の値を振って、Train Accuracy (学習データに対する精度)と__Test Accuracy__ (テストデータに対する精度)を調べたものです。(pos)は上昇側、(neg)は下落側の値です。
__Train Accuracy__の値は教科書通り、__n_estimators__を増やすと増加していきます。__Test Accuracy__の方も増えては行きますが、0.55付近で頭打ちになっています。一方、__n_estimators__の増加とともに__Test Accuracy__が減っていくという、過学習のような効果は見られません。
なお、比較の際には
kf = KFold(n_splits=n_splits, random_state=0)
clf = RandomForestClassifier(n_estimators=n_estimators, random_state=0, n_jobs=-1)
のように__random_state__を固定すると良いでしょう。また__n_jobs=-1__とすると使える最大のコア数で並列計算してくれますので、計算時間の短縮が期待できます。
次に一日あたりの平均利益 (Gain)への影響を見たのが下図です。

こちらの方も__n_estimators__とともに大きくなっていきますが、500くらいで頭打ちになっています。さらに__n_estimators__を大きくしてみましたが、顕著な依存性は見られませんでしたので、計算時間も考慮して以下では__n_estimators=500__とします。
3. thresholdの影響
次に株価が上昇/下落したと判断するためのしきい値、threshold__の影響を調べます。本来は複数のパラメーター(今回の場合だと__n_estimators__と__threshold)の両方を独立に変化させてグリッドサーチを行うべきですが、この例ではパラメーター依存性はそれほどでも無いので簡単に済ませます。
下図は__threshold__を変化させて__Gain__への影響を調べた図です。
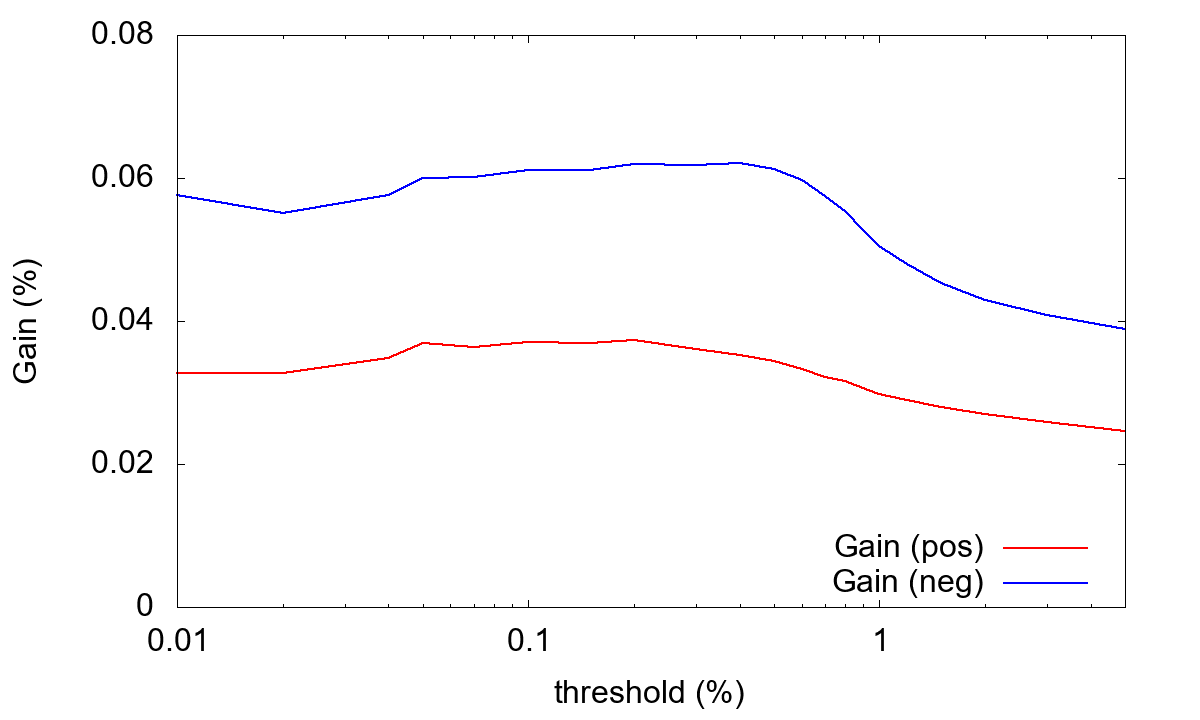
この例では__threshold__に対する強い依存性は見られません。また当然のことながらpositive側とnegative側で__threshold__依存性が違っているので、性能を追求するならpositive側とnegative側で別の__threshold__を使うと良いでしょう。以下では簡単のために__threshold=0.001__ (0.1%)とします。
またここでは__Train Accuracy__と__Test Accuracy__のプロットは作っていませんが、__Test Accuracy__は__threshold__とともに増加します。__threshold__を大きくすると当てはまるデータの割合が減るので、全部__はずれ__と予想するだけで__Test Accuracy__が改善していきます。ただしそのような予想に実用性はありません。
4. 各パラメーターの重要性
ここで学習データの各パラメーターの重要性を調べてみます。
importances = {'positive': [], 'negative': []}
df_importances = pd.DataFrame(columns_input, columns=['Row'])
(中略)
clf.fit(X_train, y_train)
importances[polarity].append(clf.feature_importances_)
(中略)
df_importances[polarity] = np.array(importances[polarity]).mean(axis=0)
print(df_importances)
のようにすると__columns_input__のそれぞれの項目の重要度を計算することができます。結果例は
Start date: 2008-01-01
End date: 2017-12-31
threshold: 0.10 %
n_estimators: 500
n_splits: 10
positive training accuracy: 1.000
positive test accuracy: 0.547±0.046
positive mean gain: 0.048±0.067 %
negative training accuracy: 1.000
negative test accuracy: 0.550±0.033
negative mean gain: 0.072±0.101 %
Row positive negative
0 N225_Open 0.168368 0.165490
1 N225_High 0.163898 0.155518
2 N225_Low 0.162818 0.162105
3 N225_Close 0.000000 0.000000
4 NYA_Open 0.174104 0.178566
5 NYA_High 0.168922 0.174139
6 NYA_Low 0.161889 0.164183
7 NYA_Close 0.000000 0.000000
のようになりました。注意しなければならないのは、それぞれの項目は__N225__または__NYA__の終値で正規化していることです。そのため__N225_Close__と__NYA_Close__の値は全て1.0になっていて、当然のことながら学習には全く役に立っていません。他の項目は0.16~0.17程度で大きな違いは見られません。強いてあげるなら__NYA_Open__の影響が少し大きいでしょうか。これはその日の__NYA__の始値と終値の比です。
5. 期間別の成績
最後に成績に期間依存性が無いか調べてみましょう。とりあえず5年くらいずつの期間に切って調べて見たのが下の表です。__期間__が2005~2009というのは、2005年1月1日から2009年12月31日までの区間のデータを使っているということです。__threshold = 0.001__で、__n_estimators = 500__としています。__Gain (positive)__と__Gain (negative)__はそれぞれ上昇側と下落側の平均利益 (一日あたり)です。
| 期間 (年) | Gain (positive) (%) | Gain (negative) (%) |
|---|---|---|
| 2003~2007 | 0.024 | 0.049 |
| 2004~2008 | 0.085 | 0.094 |
| 2005~2009 | 0.101 | 0.108 |
| 2006~2010 | 0.102 | 0.127 |
| 2007~2011 | 0.098 | 0.126 |
| 2008~2012 | 0.085 | 0.091 |
| 2009~2013 | 0.041 | 0.050 |
| 2010~2014 | 0.028 | 0.036 |
| 2011~2015 | 0.028 | 0.016 |
| 2012~2016 | 0.039 | 0.055 |
| 2013~2017 | 0.049 | 0.047 |
表を見ると、2005年から2011年あたりでは一日平均0.1 %程度の良い成績を出しているのに、それ以降は良くて0.05 %程度です。はじめはこの表を2005年から書き始めて、「昔は良かった」という結論にしようかと考えていたのですが、念のため2003~2007と2004~2008を計算してみたところ、そうでもないことがわかりました。あくまでも仮説ですが、この表で成績の良い期間はリーマンショックの期間を含んでいます。株価が急激に下がっていくときにはボラティリティと呼ばれる価格変動が大きくなる傾向にあります。そのために利益が出しやすくなっていたのでは無いでしょうか。
少なくとも今回の結果を見る限り、前回作成したプログラムは比較的長い期間に渡って安定に動作してくれそうに思えます。そこで次回は直近の期間でこのプログラムを利用していた場合、どの程度の利益 (あるいは損失)が出ていたのかシミュレートしてみたいと思います。
参考文献
- 「達人データサイエンティストによる理論と実践 Python機械学習プログラミング」 S.Raschka, 株式会社インプレス, ISBN: 978-4-8443-8060-3