（修正）Juliaで反復数値計算をしたらPythonよりも圧倒的に速かった話←そうでもなかった話

注意

この記事では最初、Juliaが劇的に速いという結論を出しましたが、検討の結果記事を修正しています。改変を加えて読みにくくなっていますが、この過程自体が速度の最適化とは何かを表していると思いますので修正部分を消さずにそのまま載せています。

やったこと

MCMC法を用いたガウス過程のパラメータ推定をPython, Juliaを使って実装し、速度を比較した

追記（190828）
「pythonでもJITコンパイル（高速化）を使えるんだからそれと比較すべきでは？」というコメントをいただいたため、python+numbaの測定結果を追加しました。

追記（190927）
コメントいただき、numbaの最適化をおこなったコードを提供いただきました。トータルでくらべると最適化NumbaのPythonの方が3倍程度早いとのこと。私の方でも検証したところ再現性が見られました。

結果

• pureなpythonとJuliaならJuliaの圧勝。

• pythonでJITコンパイル（numba）を使った場合、for　loopを用いたカーネル計算が圧倒的に高速化され、numpyを用いた配列計算より速くなった。それでもJuliaの方が速かった。

• Juliaが速いという当初の結果から一点、最適化したnumbaが一番速い

• pureな（Numba）なしのpython forループは圧倒的に遅い

• forループをやめてnumpyの配列を用いるとjuliaと同程度かそれ以上に速度が上がる
  　- numpyによる配列（行列）の一括計算は十分速い

• 関数にNumbaによるJITコンパイルを用いると速度が向上する
  　-　前述の遅いforループの速度が劇的に向上
  　-　関数の前に@numba.jitをつけるだけの手軽な処理で速度が向上する恩恵は大きい

• numbaを最適化（nopython=trueオプションをつけ、そのためにコードを若干修正）するとさらに向上

• juliaの速度が最適化されたnumbaよりも遅いのはなぜ？
  　- julia自体の最適化が行われていない可能性（@ynijiiさん談）
  　- MCMCでは乱数を生成する関数を使っており、ここの違いが現れたかも

（あくまで個人の）感想

• Julia速い
  • 配列関数にしたメリットが感じられないので他にボトルネックがある？→もっと速くなる？
• Julia書きやすい
  • 関数をドット（.）付けるだけで配列用にできるので便利
• PythonでNumpy一括処理したら結構速くなるかなと思ったが、Juliaのワーストケースに及ばなかった
  • forは問題外なのは分かった、内包表記も速くないことにちょっとショック
• numbaを試したら、forループが爆速になってビックリ、配列を一気に計算するより早い
• 速度最適化の話は結局どこまでやるかに行き着く。
  • そこまでやるならCで書くべきでは？
  • GPU使って並列計算すれば？など
  • numbaどこまで突き詰めるかは難しい問題。Pythonicな書き方を犠牲にしてまで（pythonでの）速度を優先させるか
    • 個人的な意見としてはpythonでforループを使わざるを得ないところにnumbaを使うくらいの使い方が良いと思っている
  • 行列計算（含、機械学習）やるなら大人しくライブラリ使うべき。そういう意味では今回扱う対象（ガウス過程）が不適切だったかも。。
• 細かいことを気にせず、かつ記法がシンプルなjuliaは魅力的

詳細

比較したアルゴリズム

PythonとJuliaの比較として、ここではmcmc法を使ったガウス過程のパラメータ推定を行います。理由はたまたまやっていたからです行列演算（内積、逆行列、行列式計算）を含み、さらに反復計算を行う処理であるからです。

特にMCMC法の欠点として計算時間がかかることが知られているため、Juliaでの速度向上が見込める場合は、Pythonに替えてJuliaを使う大きなモチベーションになると考えられます。
（実際の使用にはパッケージを使うべきでしょう。あくまで同じ実装をPython, Juliaで比較するためです。）

今回の記事でMCMC法やガウス過程について知っている必要はありません。単純に行列演算を含む反復過程の速度を比較したと考えてください。

比較方法

• mcmcの反復計算について、決められた反復回数（25000）にかかる時間を計測し、そこから速度(iter/sec)を算出しました。したがって、JITコンパイル時間、mcmc実行の前のデータ初期化などは計測に含まれていません。
• mcmc法は確率的な過程を含むため、原理上毎回測定時間が変わります。
  • 各項目についてn=5で計測をおこない、平均値を採用しました
• numbaを用いた場合は、階層構造になっている自作関数に関してどの関数をJITコンパイルするとパフォーマンスがでるかを事前に検証しました。（全ての関数をJITコンパイルするのが最速ではなかったため）。その中でもっともパフォーマンスが出たものを採用しています。
  • 上記に加えコメントでいただいた最適化されたnumbaの速度結果も示します

処理対象のデータ

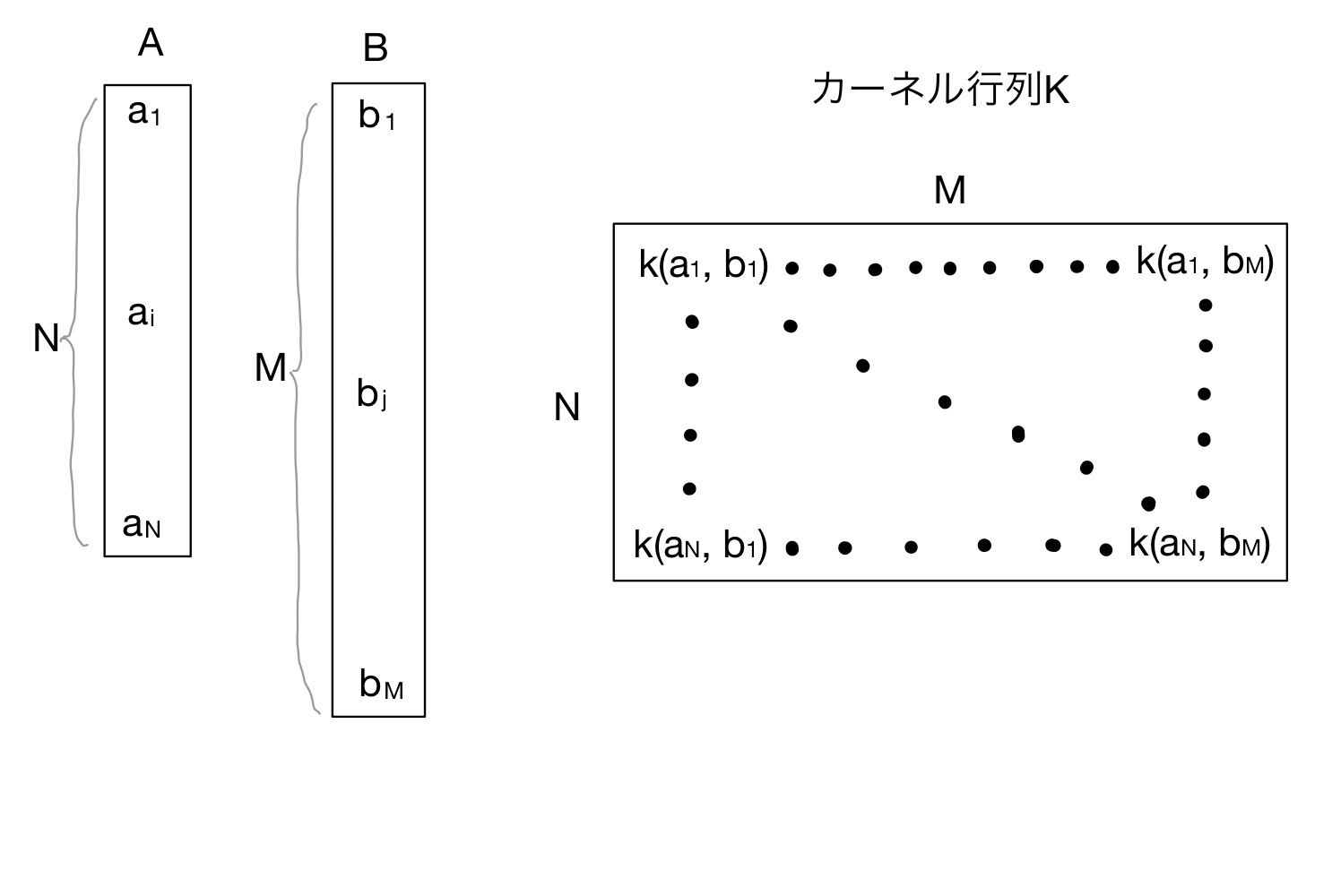
ガウス過程ではカーネル法と呼ばれるテクニックを使います。その際に2種類の1次元配列（ベクトル）から2次元の行列を作成します。

上図のように、ベクトルA（長さN）,B（長さM）から行列Kを作成します。KはN行M列の行列で、各行、列の対応する要素を入力とした関数$k(a_i, b_j)$を要素とします。この行列をこの記事ではカーネル行列$K$と呼びます。

カーネル行列の作り方

このような2次元配列をプログラムで記述する場合、ベクトルAの要素とベクトルBの要素の組み合わせを取得する必要があります。PythonとJuliaで作る場合には3つのやり方が考えられます。

1. 2重のforループ (“for”と記載)
2. 内包表記 (“list”と記載) （注：numba対応できなかったため削除しました）
3. 配列を使った処理 (“2D”と記載)

下記で説明します。

1. 2重のforループ

ベクトルAの要素をforでループしながら取得し、その中でベクトルBの要素をforループで取得する方法です。

Pythonだと

import numpy as np 
K = np.zeros((N,M))
for i in range(N):
  for j in range(M):
    K[i,j] = k(A[i], B[j]) 

Juliaだと

K = zeros(N,M)
for i = 1:N
  for j = 1:M
    K[i,j] = k(A[i],B[j])
  end
end

---

Tips. enumerate

上の全ての例では、forループのなかで配列のインデックスと配列の要素を使っています。配列の要素にアクセスするのにインデックスを使うとその都度配列にアクセスすることになり無駄な処理となります（今回はアクセスは1回だけですが。。）

Enumerateを使うと、配列のインデックスと要素を同時に取得することができます。2重forループのをenumerateを使って書き直してみましょう。

import numpy as np 
K = np.zeros((N,M))
for i,ix in enumerate(range(N)):
  for j,jx in enumerate(range(M)):
    K[i,j] = k(ix, jx) 

---

2. 内包表記

内包表記を使うことで上記の2重forループをシンプルに書くことができます。

Python

K = [[k(ix,jx) for jx in B] for ix in A]
K = np.array(K).reshape((N,M))

内包表記ではリスト（のリスト）が返ってくるので後でnp.arrayに変換します。
変数Kを初期化しておく必要はありません。そのため、forループではインデックス番号ではなく要素をそのまま参照しています。
2重forループの時とforループの順番が（見かけ上）違うことに注意しましょう。

Julia

K = [k(ix,jx) for ix in A, jx in B]

Juliaでは配列（の配列）の形で返ってくるのでそれを連結します。hcat関数を使います。
コメントでご指摘いただき、コードを変更しました。Juliaでは内包をネストしなくても一発で書けるようです。便利ですね。

3. 配列を使った処理

2重forループ、内包表記ともにベクトル内の要素を一つずつ参照して処理しています。配列をそのまま引数として計算できたら処理速度を圧倒的に高速化することができます。

Pythonの場合

Pythonの場合。numpyの関数をうまく使います。
例えばN行M列の行列で要素ごとの引き算を行いたい場合

A - B.T

と横にしたいベクトルの転置を取れば2次元行列の各要素がAとBの対応する要素の引き算となります。

これを用いれば例えばガウス基底のカーネル関数を

def k_for_array(A,B):
  C1 * np.exp(-1 * np.power((A - B.T),2)/C2)

K = k_for_array(A,B)

のように配列用の関数としてうまく作ることができます

Juliaの場合

Juliaの場合はもっと簡単です。スカラ用のカーネル関数$k(a_i, b_j)$がある場合、ドット(.)を付けることで配列用の関数に変えることができます。

K = k.(A, transpose(B)) 

このように、スカラ用の関数があれば配列用の関数をわざわざ作らなくてもよいところがPythonとの違いでJuliaの良いところだと思います。

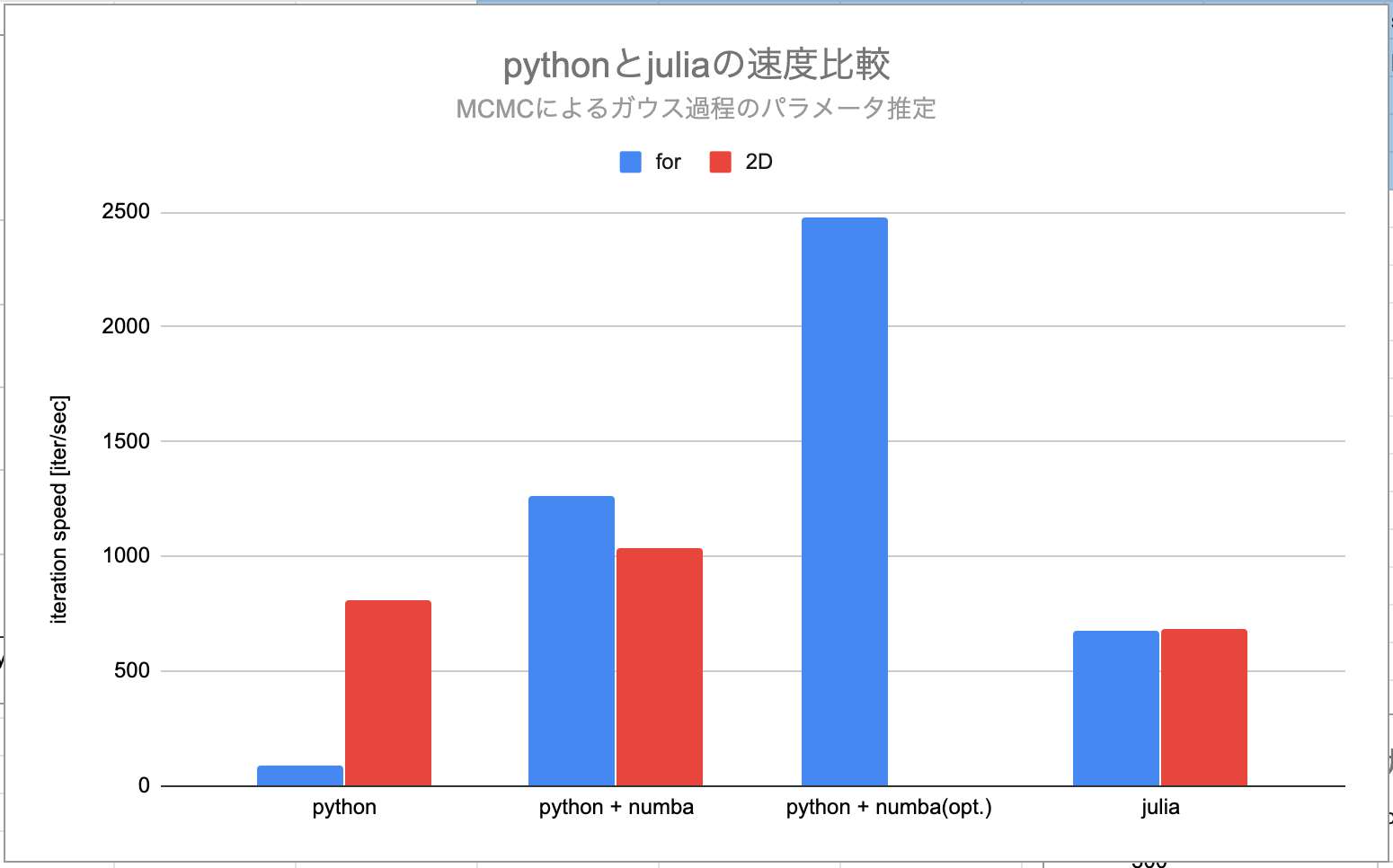
計算結果

処理結果を載せます。同じ条件（N=20, M=100, MCMCの反復回数=25000）で処理を行い、1秒あたりのMCMC反復回数(iter/sec)で比較しました。数値が高い方が処理が早くなります。

全ての条件でJuliaの方が高い速度を示しています。
forループを用いた場合、numbaを用いることで劇的に速度が向上しています。対照的に2Dの場合はあまり速度が向上しません。これはnumpy配列関数はすでにBLASで高速化されているので、JITコンパイルの恩恵が見られなかったと考えられます。listに関してはnumbaを使うとエラーが出てしまうため、検証できませんでした。（内包表記はnumbaに対応していないのか？）

JITコンパイルをする関数

numbaのJITコンパイルでは（自作）関数の上に@numba.jit (import numbaの場合。from numba install jitの場合は@jit)をつけることで、該当の関数をJITコンパイルします。forループを用いたカーネル行列作成の場合、関数の構成は

1. mcmcループ(for使用)
   1. mcmcロジック（while使用)
   2. ガウス過程（行列演算）
   3. 最終的なカーネル関数Kの出力 　5. 2Dのカーネル関数行列Kの作成(2重forループ）
      　 6. 単一のカーネル関数定義

のように上の関数から下の関数を呼び出しています。最適化したい関数は5の部分の2重forループでおよび、1,2のループ部分です。

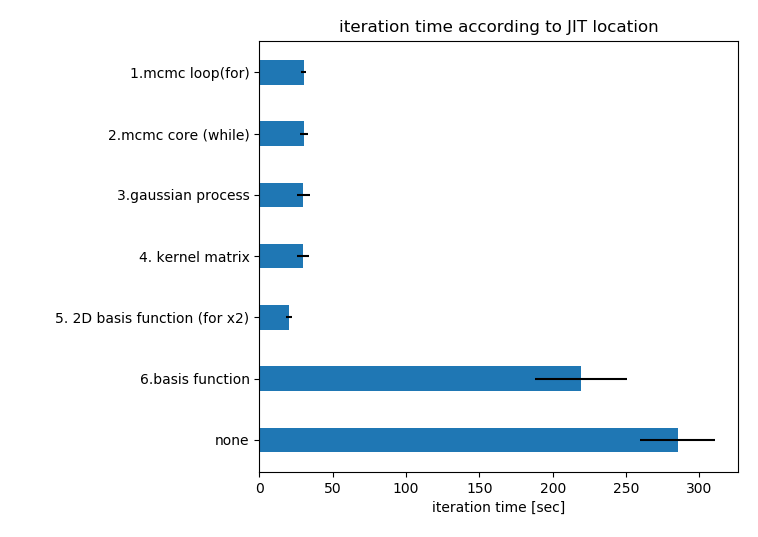
このとき、最下層の関数からJITコンパイルを付け加えて行ったときの反復時間の変化を下図に示します。

このグラフの読み方は、例えば4.kernel matrixの測定値は4の関数以下(つまり5,6も)JITコンパイルしている、というように読んでください。noneはJITコンパイルを全く使っていない状態です。

下から見ていきましょう。noneに比べて最下層の6.単一の関数定義を最適化することで50秒ほど短縮しています。この関数の出力がカーネル行列の各要素となり大量に計算が行われるためです。

もっとも劇的に速度が向上し、反復時間が減少したのが5（および6）をJITコンパイルしたときです。頻繁に呼び出されるカーネル関数の定義および、その（2重forループでの）呼び出し方をJITコンパイルしておくことで、forループを使っても劇的な速度の向上が見られました。それにより、numpyの配列関数（"2D"と書いた手法）よりも速度が向上したのは、前述した通りです。

それより上位の関数もJITコンパイルしたところ逆に反復時間がかかる結果になりました。どこまで上位のものをコンパイルしても反復時間はほぼ同じで横並びです。JITコンパイル何かオーバーヘッドとなる処理が発生しているようです。

結論としては、JITは最適化したい関数とその関数が読んでいる関数をコンパイルする必要があります。

ちなみに5だけをJITコンパイルしたとき（すなわち6をしていないとき）、速度は全然改善しません。
（他の条件も知りたい方はコメントください。）

（さらに）最適化されたnumba関数

コメント欄の@ynijiさんのコードを参照ください

おまけ

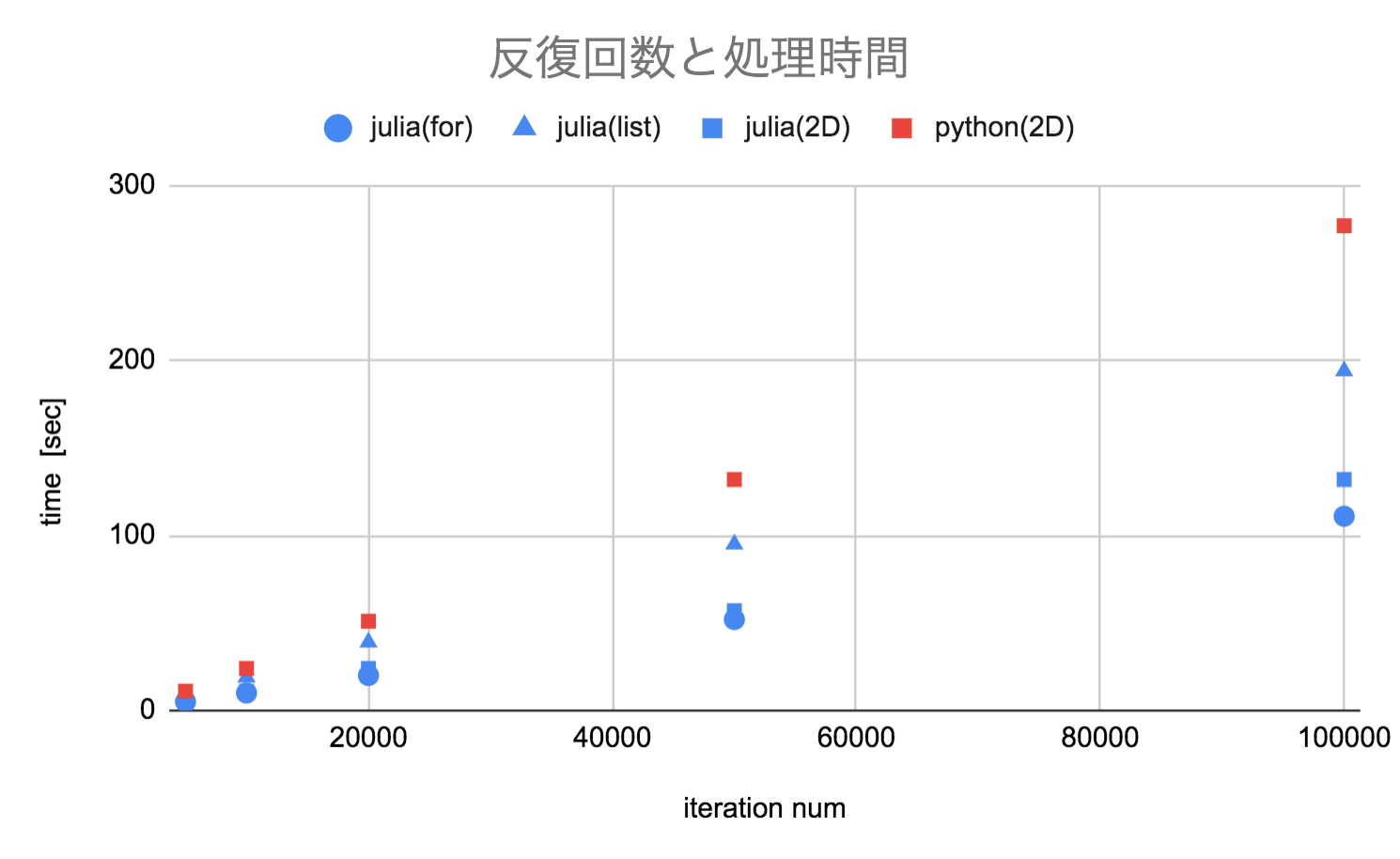
反復回数と処理時間

N=20, M=100で固定して反復時間を振ってみました。

反復回数にともない線形に増加しています。

サンプル数と処理時間

今回実装したガウス過程のアルゴリズムでは内部で行列式の計算を行なっています。サンプル数Nにしたがって指数関数的に処理時間が増えます。サンプル数が大きいところではjuliaの各処理の差は（つまり上の棒グラフで示したような差は）ないようにも見えます。

今後

実装は近日中に整理して公開します。