はじめに
こんにちは。物工/計数 Advent Calendar 2021の17日目です。
今日は制御工学という分野について、gifアニメーションを交えて紹介していきます。
実はいま、計数工学科では、学生有志が計数をもっと知ってもらえるエキサイティングなブログを作成しています。この記事もそのブログで公開される予定です。他にも計数工学について分かりやすく解説した記事や計数工学を題材にしたゲームを公開する予定なので、工学博覧会のツイッターをフォローして続報をお待ちください!
制御工学とは
制御とは、 対象を自分の思いのままに操る ことです。英語で コントロール と言ったほうがピンと来る人も多いのでしょう。制御工学の応用範囲は広く、工学の多くの場面で使われています。
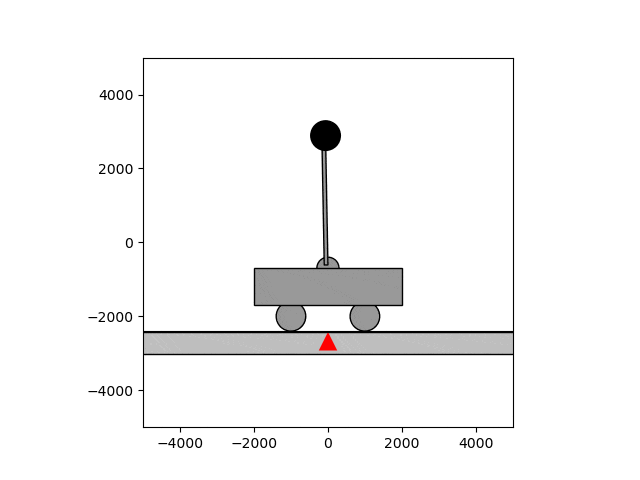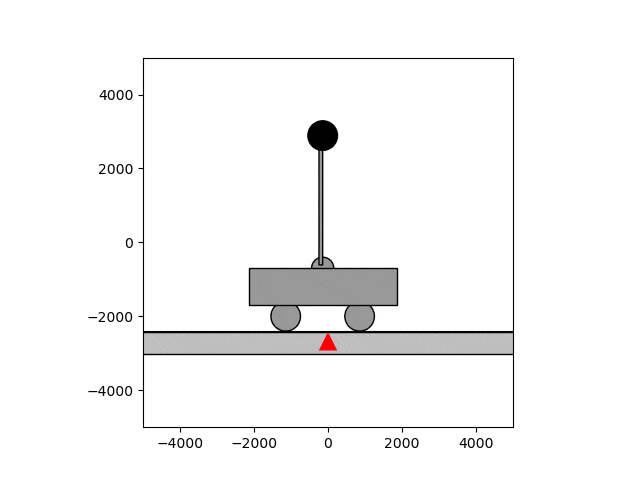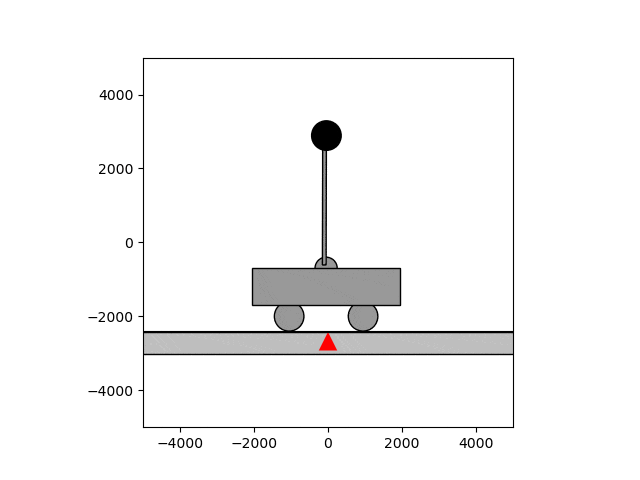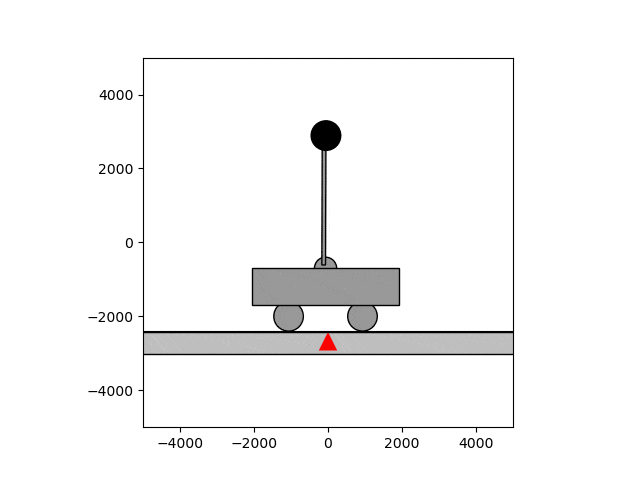
倒立振子
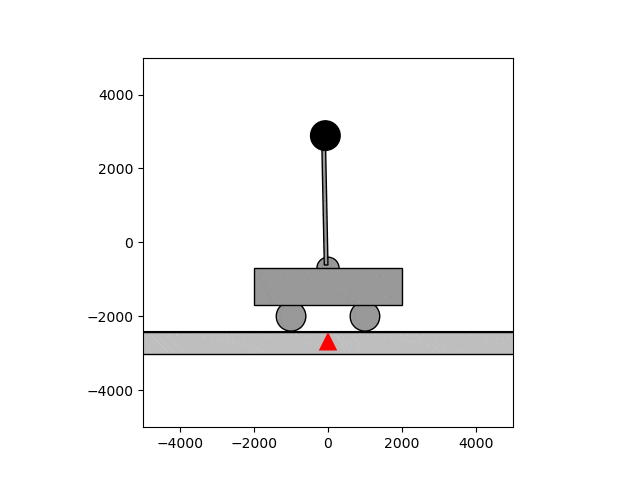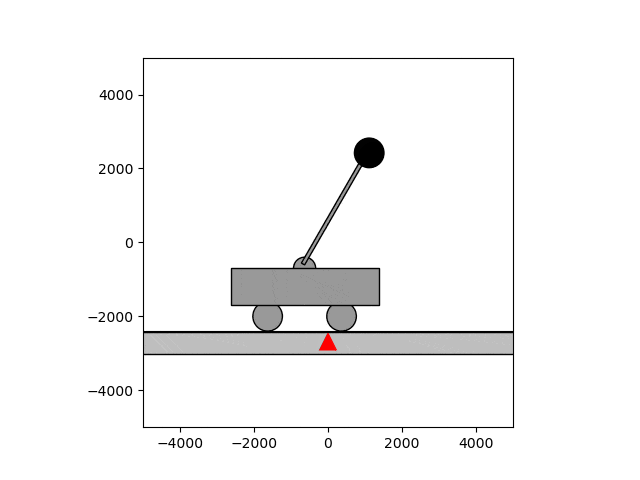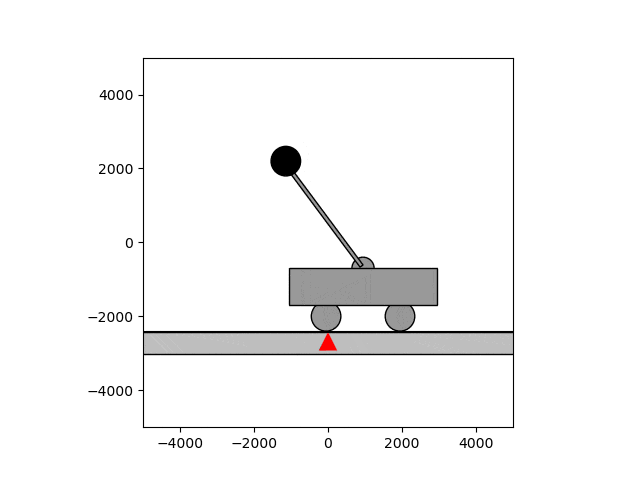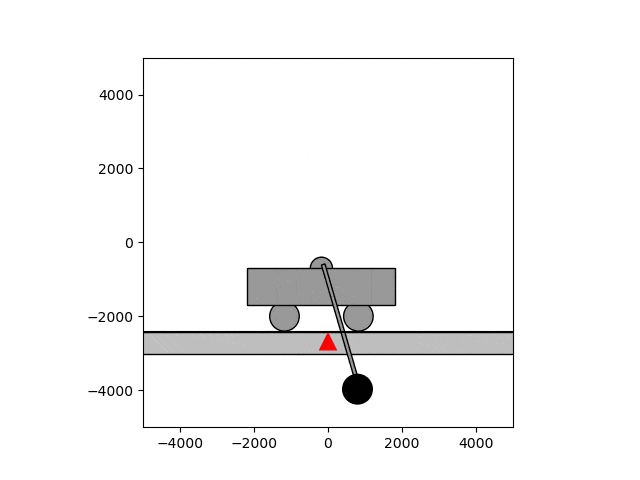
倒立振子は制御の定番で、計数工学科の実験でも扱います。台車に振り子が付いていて、振り子を逆さに立てたいというのが倒立振子の状況設定です。当然ですが、放っておけば振り子は倒れてしまいます。
そこで制御の出番です。フィードバック制御を用いると、しっかりと逆さに立てた状態で保つことができます。下のgif画像はほぼ動いていないように見えますが、これは制御によって保っているためです。
フィードバック制御
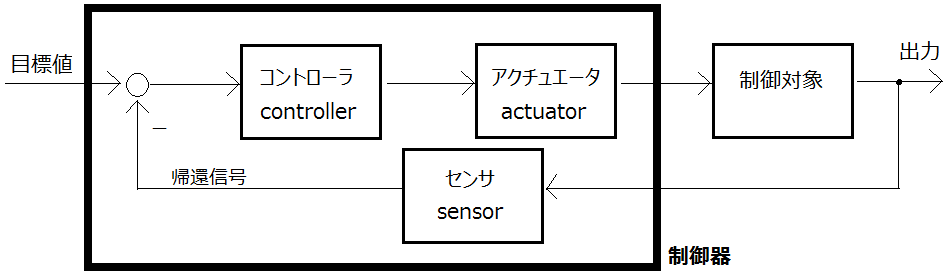
フィードバック制御の枠組みは下のような図で表されます。
制御器の目標は制御対象の状態を目標値に一致させることです。そこで制御器はまず制御対象の状態をセンサで計測し、目標値との差分$e(t)$を計算します。制御器はアクチュエータを通じて制御対象に影響を与えることができるので、差分$e(t)$を$0$にするためにアクチュエータにどのような司令を出せば良いのか計算します。
古典制御理論
制御器の設計については、制御理論の中で出来るだけ速く、そして安定に目的の状態を達成するシステムを目指すという観点から、様々な検討と改良が行われてきました。今回はドローンを飛ばすことを通じて、様々な制御手法を試してみましょう。ドローンが赤い線に乗るのが目標の高さです。
BangBang制御
最も単純な制御は、出力が目標値に到達しない間は制御入力を与え、目標値を上回れば入力をオフにする、ON/OFF制御です。ON/OFF制御は専門用語では BangBang制御(バンバン制御) と呼ばれています。ちょっと語感が面白いですね。
赤い線より下ならプロペラを回して、赤い線を上回ってたらプロペラを止める制御でドローンを飛ばしてみましょう。
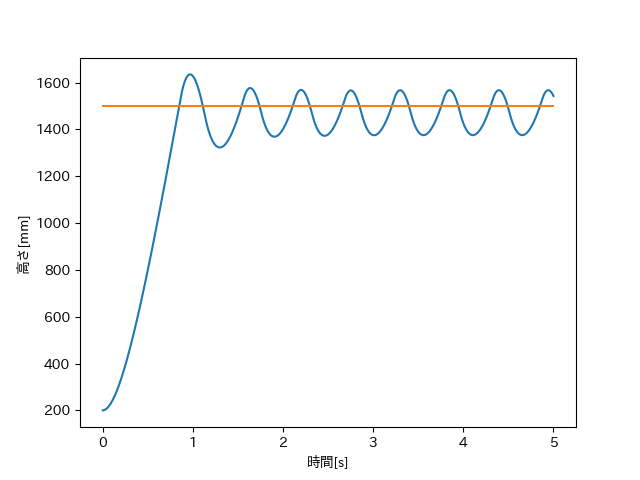
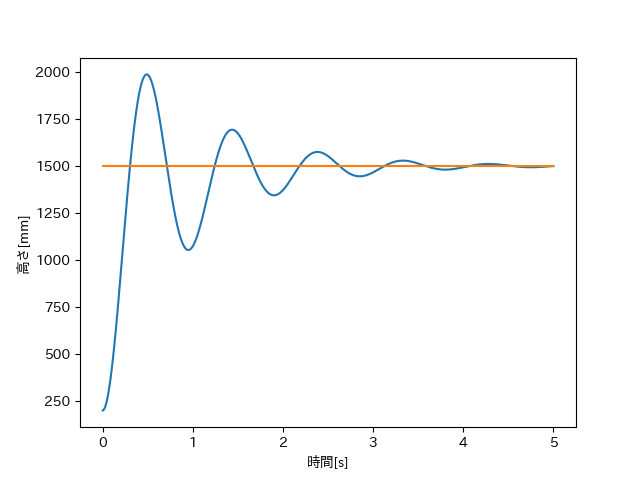
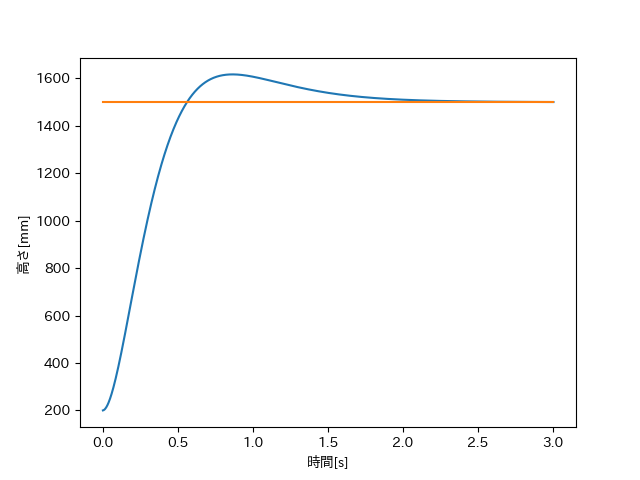
だいたい目標高さ付近に制御できていますが、下の高さの時間グラフを見ると高さが上下し続けていることが分かります。
グラフを見てみると振動幅が減少してないので、いつまでも目標値付近で振動することが予想されます。これでは安定に出来たとは言えないでしょう。
BangBang制御が有効な例として、冷房が挙げられます。部屋の温度が多少上下しても気にする人は居ないでしょう。なので、例えば、冷房の設定温度が28℃だったら室温が28℃以下のとき冷房を止め、室温が28℃以上のとき冷房を稼働させる制御によって室温をだいたい28℃付近に保つことが出来るでしょう。
P制御
出力と目標値との差分 $e(t)$ に比例した制御入力を用いる制御を、P制御といいます。Pは比例(proportional)の頭文字です。偏差を$e(t)$で表すとき、制御入力$u(t)$は正の比例ゲイン$K_\mathrm{P}$をパラメータとして、
$$
u(t) = K_\mathrm{P} \cdot e(t)
$$
で与えられます。
BangBang制御では目標値付近になっても0%か100%の制御入力しかできなかったことにより目標値付近で振動が続きましたが、P制御では微調整ができるため状態が一定の値に収束させられるのではないかと期待できます。
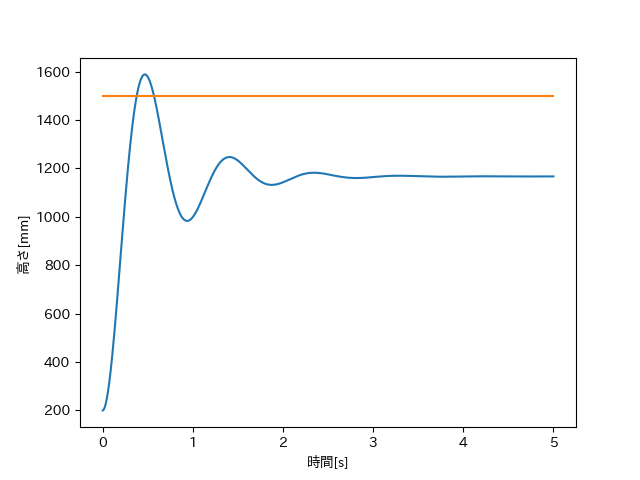
たしかに状態は収束していますが、その収束値は目標からずれた値をとっています。これは目標値に近づくほど制御入力が小さくなり、外乱(この場合は重力)の影響を打ち消すことができないためです。それでも定常偏差を0に近づけようとゲインを大きくしていくと、今度はシステムの応答が振動的になり過ぎて発散してしまいます。
PI制御
定常偏差を0にするため、積分器による制御(integral control)を導入します。偏差を時間積分して制御入力に加えてみます。こうすると定常偏差を打ち消すような制御入力が加わり、目標値に収束することが期待できます。制御入力は次のように表せます。
$$
u(t) = K_\mathrm{P} e(t) + K_\mathrm{I} \int_0^t e(\tau) d \tau
$$
PI制御でドローンを飛ばしてみましょう。
今度は重力の影響がきちんと補償されてちゃんと赤い線に乗りました。ただ、きっちり収束するまでに何度か線を通り越しています。
PID制御
応答の速さを改善するため、微分器による制御(differential control)を加えます。比例、積分器も組み合わせた3項制御のことをPID制御といい、制御入力は次のように定式化されます。
$$
u(t) = K_\mathrm{P} e(t) + K_\mathrm{I} \int_0^t e(\tau) d \tau + K_\mathrm{D} \frac{d e(t)}{d t}
$$
微分項が含まれることで、急激な目標値の変化や外乱に対して素早く反応して制御入力に反映されるため、より速く目標値へ収束します。
PID制御でドローンを飛ばしてみましょう。ちゃんと赤い線に乗るように収束している上、収束も速くなっていることが分かります。
高さのグラフを見てみましょう。PI制御では目標を大幅に踏み越していましたが、微分器を導入することでこれが抑制されていることが分かります。
さまざまな制御理論
今回はPID制御を紹介しましたが、制御理論については他にも様々なアプローチで研究されています。
現代制御理論
先程のドローンの系はPID制御によって高性能な制御を行うことができました。PID制御は非常に実用的で、世の中の半分以上のシステムがPID制御によって制御されていると言われています。しかし、PID制御はシステムが大規模・複雑になったときの対処ができないという問題があります。例えば、最初の倒立振子の例はどうでしょうか。倒立振子を立ててかつ真ん中に留めておきたいといった複数の要請があったとき、どのように制御をすればいいのでしょうか?これに答えられるのが現代制御です。
現代制御理論では線形システムを制御という観点から解析することで本質的な構造を解き明かすことを目標としています。可制御と可観測の双対性など、システムの構造に関する美しい定理がいくつか知られています。
最適制御
最適制御とは、なにかの指針となる値(評価関数)を最小になるような制御です。評価関数は、例えば電力と偏差の大きさに重み付けをして足し合わせたた値であったり目的の位置で止まるまでの時間など、制御する目的に応じて設定します。実は最初にお見せした倒立振子の例も、LQRという最適制御を用いて制御しています。この手法は評価関数を決定してしまえば制御器が設計できるため、PID制御におけるパラメータ調整の代わりに評価関数を設計することになり、より目的に沿った制御器を設計しやすくなります。
ロバスト制御
実際のシステムと数理モデルの間にはモデル化誤差と呼ばれる誤差があります。この要因は様々な場合があり、複雑なシステムを簡単な数理モデルで近似している場合や、解析が困難なほど複雑な数理モデルを簡易化した数理モデルを用いている場合、モデルのパラメータ推定(システム同定)の誤差などが主な要因として挙げられます。このモデル化誤差のために実際のシステムの性能が劣化してしまったり、時には不安定になってしまう場合すら考えられます。このような場面で「この範囲の誤差なら必ず安定にしますよ」といった保証を行うのがロバスト制御です。
参考文献
[1] 杉江俊治, 藤田政之, 『フィードバック制御入門』, コロナ社, 1999.
[2] MathWorks, 『PID制御』、https://jp.mathworks.com/discovery/pid-control.html.
[3] 2018年度工學博覧会理論冊子 『フィードバック制御系』
リンク
このページのシミュレーションはgithubにて公開しています