概要
学生実験などでレポートを書く時には、手軽に使えるExcelを使う機会も多いと思います。
Excelを使えば、グラフも簡単にかけ、簡単なグラフであれば、近視曲線まですぐに計算してくれて便利ですよね。
多項式で近似できる曲線であればよいのですが、指数関数とか対数関数とかだと
Excelで近似曲線を出そうと思ったら少しコツが必要だったり、Excelでは計算できないなんてこともありますよね。
今回は、電気回路などでよく出てくる過渡現象の近似曲線をPythonを使って計算し、近似曲線の式まで
計算してみようと思います。これでexpを含む式もすぐに近似できるようになりますね。
動作環境
- Windows10(64bit)
- Python 3.7.2
近似曲線を計算する関数
Pythonには、近似曲線を計算できる関数がいくつかあるようです。
結論から言うと、scipy.optimizeのcurve_fitを使うといいと思います。
Pythonで近似曲線を計算してくれる関数は主に以下の3つがあるようです。(そのほかにもいくつかありそうです)
方法は全て最小二乗法っぽいです.
- numpy.polyfit()
- scipy.optimize.leastsq()
- scipy.optimize.curve_fit()
一つずつ順番に説明していきます。
- numpy.polyfit()
これは名前からもわかるように多項式(polynomial)で近似する関数です。なので、非常に簡単に使える反面、使える場面が限られてくると思います。
使い方は簡単で、第一引数に独立変数xの配列、第二引数に従属変数yの配列、第三引数に近似式の次数(degree)を取ります。
返り値は、近似多項式の係数(coefficient)で、高次のものから低次のものの順になります.
たとえば,以下のように使います.
x = np.array([1,2,3])
y = np.array([2,7,16]) # y=2x^2-x+1
coeff = np.polyfit(x, y, 2) # coeff = [ 2. -1. 1.]
- scipy.optimize.leastsq()
これは名前からまさに最小二乗法っぽいですね.ただ,この関数使い方が少し独特だと私は感じました.
引数は2つ.第1引数は関数,第2引数は推定における初期値です.返り値は,係数の配列と次数のようです.
たとえば,以下のように使います.
x = np.array([1,2,3])
y = np.array([2,7,16]) # y=2x^2-x+1
def func(param, x, y):
residual = y -(param[0]*x**2 + param[1]*x + param[2])
return residual
param[0,0,0]
coeff = optimize.leastsq(func, param, args = (x, y)) # coeff = (array([ 2., -1., 1.]), 2)
- scipy.optimize.curve_fit()
最後に本命のcurve_fit()です.
使い方は,第1引数にパラメータをもつ関数,第2引数に独立変数x,第3引数に従属変数yを取ります.
返り値は,近似式のパラメータの配列と共分散です.
具体的には以下のように使います.
x = np.array([1,2,3])
y = np.array([2,7,16]) # y=2x^2-x+1
def func(x, a, b, c):
return a*x**2 + b*x + c
param, cov = curve_fit(func, x, y)
# param = [ 2. -1. 1.]
# cov =
[[inf inf inf]
[inf inf inf]
[inf inf inf]]
コード
では,早速実装していきましょう.
from scipy.optimize import curve_fit
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
def fit(x,K,T):
return K*(1-np.exp(-x/T)) # 近似したい関数の式
K = 10 # 比例定数
T = 1 # 時定数
list_x = range(11)
array_x = np.array(list_x)
list_y_data = []
for num in array_x:
list_y_data.append(K*(1-np.exp(-num/T)) + np.random.rand())
array_y_data = np.array(list_y_data)
param, cov = curve_fit(fit, array_x, array_y_data)
print(param)
array_y_fit = param[0] *array_x + param[1]
list_y_fit = []
for num in array_x:
list_y_fit.append(param[0]*(1-np.exp(-num/param[1])))
array_y_fit = np.array(list_y_fit)
sns.pointplot(x=array_x, y=array_y_data, join=False)
sns.pointplot(x=array_x, y=array_y_fit, markers="")
plt.show()
解説
- フィッティングしたいデータの作成
list_x = range(11)
array_x = np.array(list_x)
list_y_data = []
for num in array_x:
list_y_data.append(K*(1-np.exp(-num/T)) + np.random.rand())
array_y_data = np.array(list_y_data)
まずは,フィッティングしたデータを用意します.実験を行ったのであれば,そのデータになりますが,
今回は,フィッティングの精度も確かめたいため乱数を使ってデータを作成します.
np.random.rand()で0.0以上1.0未満の一様分布の乱数を発生できます.
- フィッティングを行う
param, cov = curve_fit(fit, array_x, array_y_data)
print(param)
array_y_fit = param[0] *array_x + param[1]
list_y_fit = []
for num in array_x:
list_y_fit.append(param[0]*(1-np.exp(-num/param[1])))
array_y_fit = np.array(list_y_fit)
先に述べたcurve_fit()を用いてフィッティングを行います.
実行結果
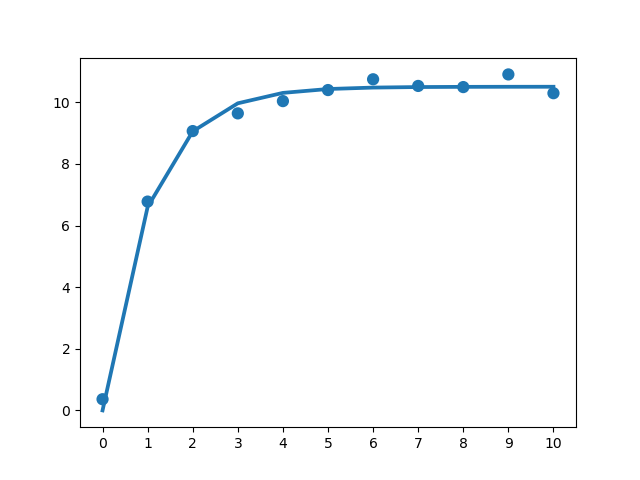
実行結果は以下のようになりました.乱数を用いているので,実行時によって結果は多少変わると思います.
今の場合,
coeff = [10.5086373 1.00943089]
となっています.うまくいっていますね.
まとめ
いかがだったでしょうか?今回は過渡現象のフィッティングを行ってみました.
次はもっと複雑な関数の近似を行ったり,物理現象に限らず回帰分析分野にも
挑戦していきたいと思います.
今回のコードのなどについて改善点や建設的なフィードバックなどありましたらコメントに書いていただけると
助かります!