概要
フーリエ変換を離散化したものが離散フーリエ変換(DFT)であり、
計算機ではこのDFTを高速化した高速フーリエ変換(FFT)を用いて、
フーリエ変換をしています。
DFTの練習問題としてよく出てくるのが,
(1)方形波
(2)正弦波
の2つです.
正直フーリ変換と違ってDFTは手計算できるものがかなり限られてくるので
この2つを押さえておくだけでもだいぶ違うかなと思います.
前回は(1)方形波を扱ったので,今回は(2)正弦波を扱おうと思います.
[【信号処理】Pythonを使って方形波をフーリエ変換してみた!]
(https://qiita.com/trami/items/2d893d781eaeb75025b1)
DFTを実際に手計算で計算し,それをPythonでFFTしたものと一致するかを確かめてみたいと思います.
動作環境
- Windows10(64bit)
- Python 3.7.2
DFTの復習
入力信号をx(n)とすると,そのDFTであるX(k)は以下のようになります.ただし,$W_N = exp(-j\frac{2\pi}{N})$.
X(k) = \sum_{n=0}^{N-1}{x(n)W_{N}^{kn}}
問題
x(n) = cos(2\pi ft)
のDFTを求めなさい.ただし,サンプル数$N=8$,周波数$f=1000$,$t=nT=n\times\frac{1}{1000N}$とする.
解答
それでは上記の問題を,まずは手計算で計算していきます.
まずは,回転子を導入する.
W_8 = exp(-j\frac{2\pi}{8})
回転子を用いると,入力信号は以下のように表される.
x(n) = \frac{1}{2}(W_8^{-2n}+W_8^{2n})
DFTの定義より
\begin{align}
X(k) & = \sum_{n=0}^{7}x(n)W_8^{kn}\\
& = \frac{1}{2}\sum_{n=0}^{7}(W_8^{-2n}+W_8^{2n})W_8^{kn}\\
& = \frac{1}{2}\sum_{n=0}^{7}W_8^{(k-2)n}+\frac{1}{2}\sum_{n=0}^{7}W_8^{(k+2)n}\\
& =\begin{cases}
& 4 & (k = 2, 6)\\
& 0 & (otherwise)
\end{cases}
\end{align}
実装
では,早速実装していきましょう.
import numpy as np
import matplotlib.pyplot as plt
pi = np.pi
N = 64
f = 1000
n = np.array(range(0,N))
t = n/(1000*N)
f = np.cos(2*pi*f*t)
F = np.fft.fft(f)
fig = plt.figure()
ax1 = fig.add_subplot(211)
ax2 = fig.add_subplot(212)
ax1.stem(n, f)
ax2.stem(n, np.abs(F))
ax1.set_xlabel('t')
ax2.set_xlabel('k')
ax1.set_ylabel('f')
ax2.set_ylabel('abs(F)')
fig.tight_layout()
plt.show()
解説
特に難しいところはないと思います.
高速フーリエ変換はnp.fft.fft()でできます.
グラフ描画は離散データなので,stemで描画するためnp.stem()となります.
実行結果
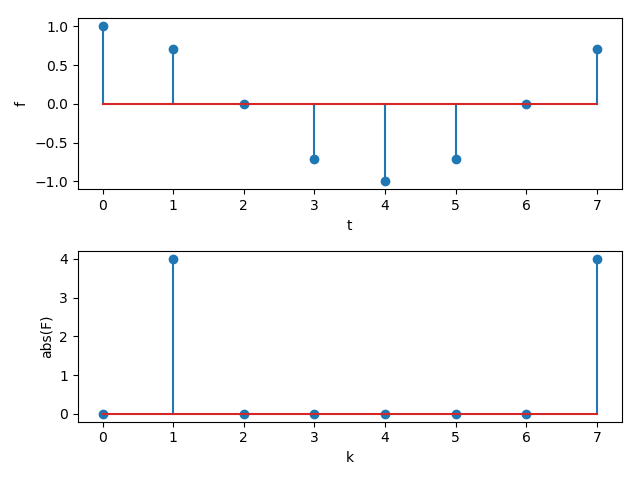
以上のプログラムを実行すると以下のような画像が得られます.
$k = 7$の成分は$k = -1$の成分と解釈することもできますね.
今回は入力信号の角周波数が単一なので,プラスとマイナスの所に2つインパルスが立っていますね.
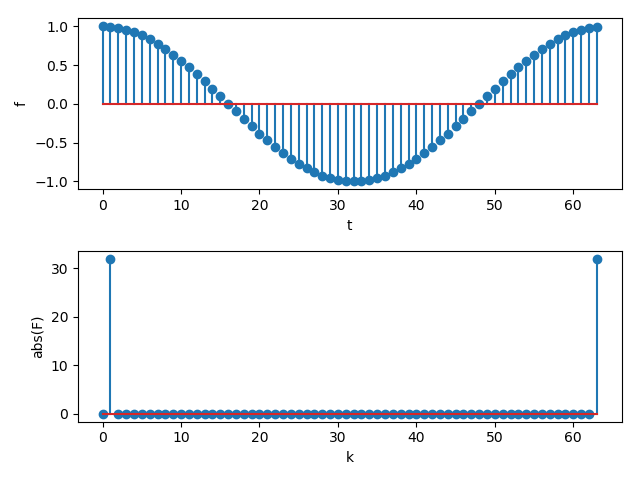
サンプル数を増やして$N=64$として実行した結果が以下になります.
まとめ
今回は,DFTで頻出の正弦波のDFTに挑戦してみました.いかがだったでしょうか?
計算に関してはほぼお決まりのパターンなので,たくさん練習をして慣れていくといいと思います.
サンプル数を変えたり,入力信号を変えたりして遊んでみると面白いのではないかなと思います.
今回のプログラムに関して何か改善点や建設的な意見等あればコメントしてもらえると助かります!