概要
今回は,半導体などを扱うとすると必ず出てくるフェルミ・ディラック分布関数をはじめとする
さまざまなエネルギー分布関数をPythonを使って描画してみようと思います.
動作環境
- Windows10(64bit)
- Python 3.7.2
エネルギー分布関数
熱平衡状態において,ある特定のエネルギーを持つ粒子数と量子数(状態数)との割合を与えるものがエネルギー分布則であるが,エネルギー分布則は以下の3つに大別できる.
- マクスウェル-ボルツマン分布則
→ 一つの量子状態に何個の粒子が入ってもよく,しかもそれぞれの粒子は互いに区別できる.
f(E)=\exp(\frac{E_F-E}{k_B T})
- ボーズ-アインシュタイン分布則
→ 一つの量子状態に何個の粒子が入ってもよいが,それぞれの粒子は互いに区別できない.
f(E)=\frac{1}{\exp(\frac{E-E_F}{k_B T})-1}
- フェルミ-ディラック分布則
→ 一つの量子状態には1個の粒子しか入ることが許されず,しかも粒子が互いに区別できない.
f(E)=\frac{1}{\exp(\frac{E-E_F}{k_B T})+1}
上記の導出など細かい部分はさておき,今回は上記の分布をPythonで描画していこうと思います.
コード
では,早速実装していきましょう.そんなに難しくはないです.
簡単のため,パラメータは0や1にしておきました.
また,ボーズ-アインシュタイン分布では,$E=E_F$で発散してしまうため,一工夫してあります.
"""エネルギー分布関数を描画するプログラム"""
import numpy as np
import matplotlib.pyplot as plt
k = 1 # ボルツマン定数
Ef = 0 # フェルミ順位
T = 1 # 温度
# マクスウェル-ボルツマン分布
def Maxwell(E):
return np.exp((Ef-E)/(k*T))
# ボーズ-アインシュタイン分布
def Bose(E):
return 1 / (np.exp((E-Ef)/(k*T)) - 1 )
# フェルミ-ディラック分布
def Fermi(E):
return 1 / (np.exp((E-Ef)/(k*T)) + 1 )
E = np.linspace(-3, 3, 100)
E_ = np.linspace(0, 3, 100)
y1 = Maxwell(E)
y2 = Bose(E_)
y3 = Fermi(E)
fig = plt.figure()
ax = fig.add_subplot(111)
c1,c2,c3 = "blue","green","red"
l1,l2,l3 = "Maxwell","Bose","Fermi"
ax.set_xlabel(r'$\frac{\epsilon-\mu}{k_BT}$')
ax.set_ylabel(r'$f(\epsilon)$')
ax.set_title("Energy Distirbution Function")
ax.grid()
ax.set_xlim([-3, 3])
ax.set_ylim([0, 4])
ax.plot(E, y1, color=c1, label=l1)
ax.plot(E_, y2, color=c2, label=l2)
ax.plot(E, y3, color=c3, label=l3)
ax.legend(loc=0)
plt.show()
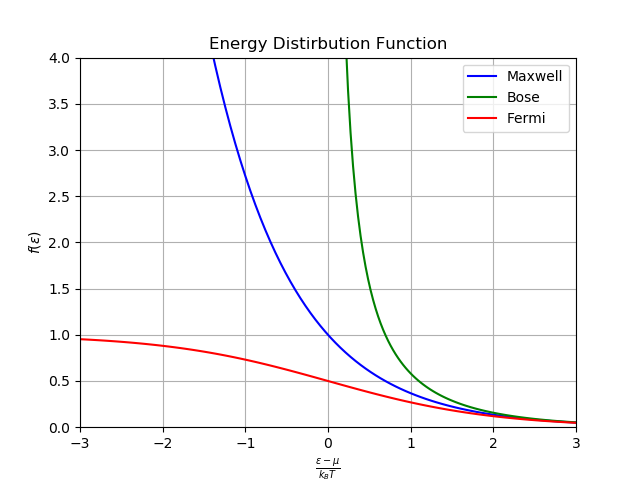
実行結果
まとめ
いかがだったでしょうか?今回は3つのエネルギー分布を描画してみました.
古典極限においては,3つの分布関数がほぼ一致することが確認できましたね.
今回のコードに関して何か改善点などあればコメントいただけると助かります.