Pythonによるランダムウォークのメモです。ちょっと数式書いてますけど、数学的には厳密ではありませんので悪しからず。
単純ランダムウォーク
時刻$n$における価格$p(n)$を、
$$p(n) = p(n-1) + d(n)$$
のように1サンプル前の価格$p(n-1)$に$d(n)$(ただし、$d(n)$は$1$か$-1$)を加えて算出していく時系列を単純ランダムウォークといいます。
まず、$d(n)$はPythonで次のように書けます。
%matplotlib inline
import numpy as np
import pandas as pd
dn = np.random.randint(2, size=1000)*2-1
0か1の乱数を生成して、2倍して1を引くと、-1か1になるということです。あるいは、次のように[-1,1]のどちらかをランダムで選ぶ書き方もできます。
dn = np.random.choice([-1,1], size=1000)
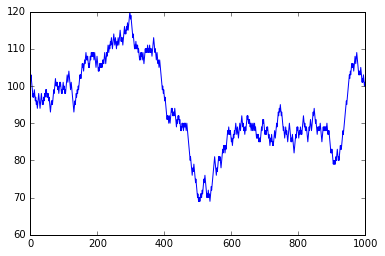
これを順番に足し合わせていけば、単純ランダムウォークとなります。ここでは、初期値$p(0)=100$としておきます。
p0 = 100
swalk = np.cumsum(dn)+p0
pandasのSeriesクラスにしてプロットしてみます。
pd.Series(swalk).plot()
幾何ランダムウォーク
単純ランダムウォークは、一つ前の価格に$+1$か$-1$を加えるものですが、これを続けていくと、価格がマイナスになることがあります。株価がマイナスになるのはおかしいので、実際の株価の動きをシミュレーションするために、単純ランダムウォークをちょっと変形した幾何ランダムウォークというのを使います。
幾何ランダムウォークは、価格の代わりに価格の対数値を使って同じような式を立てます。
$$\log p(n) = \log p(n-1) + d(n)$$
この式で、$\log p(n-1)$を移項して
$$\log\frac{p(n)}{p(n-1)}= d(n)$$
両辺のexp()をとると、
$$\frac{p(n)}{p(n-1)}=e^{d(n)}$$
となります。つまり、$p(n-1)$から$p(n)$を求める式は
$$p(n)=e^{d(n)} p(n-1)$$
となります。ここで、$d(n)$が小さいときに$e^{d(n)} \approx 1+d(n)$と近似できることから、$d(n)$が前のサンプルの価格からの変化率となっていることがわかります。
ただし、$d(n)$が変化率だとすると、$+1$や$-1$だと、100%の変化率となってしまい大きすぎます。ここでは、100円に対する1円の変化が1%ということから、$d(n)$は$0.01$か$-0.01$にして計算します。単純ランダムウォークで求めたdnを使うと、同じく初期値$p(0)=100$として
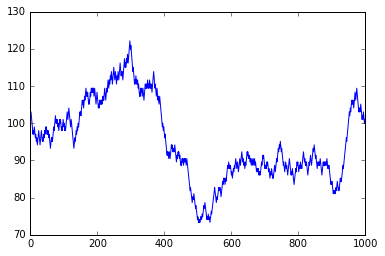
gwalk = np.cumprod(np.exp(dn*0.01))*p0
のようにexp(dn*0.01)を順番に掛け合わせていけばOKです。これをプロットすると次のようになります。
pd.Series(gwalk).plot()
単純ランダムウォークと同じ$d(n)$を使っているので、見た目はだいたい同じですが、1円単位で変化するか、1%単位で変化するかの違いが100円から離れたところで多少表れています。
実際の相場に近いランダムウォーク
株式でもFXでも、実際の相場は正確にはランダムウォークではありませんが、ランダムウォークに近いものとして考えることができます。ここでは実際の相場に近いものをランダムウォークで作ってみます。
幾何ランダムウォークでパラメータとなるのが、変動率です。先ほどの例では1サンプルあたりの変動率を1%にしましたが、相場の世界では、1年単位の変動率の標準偏差を「ボラティリティ」という言い方で表します。以下は、実際のFXのボラティリティを表示したサイトです。
ボラティリティが10%というのは、1年後に価格が$\pm 10$%に収まる確率が正規分布の$\pm 1\sigma$の範囲(だいたい68%)という意味なのですが、実際ボラティリティは時間とともに変動します。ボラティリティを変動させるランダムウォークのモデルもありますが、ここではボラティリティは固定しておきます。FXの場合、ボラティリティは10%から20%くらいなので、今回、15%としてみます。
次に、毎回同じ変化率で変化していくのは実際の相場ではあり得ません。そこで、変化する時間枠を細かくしていきます。例えば、1分間隔でランダムウォークを実行すると、1時間で60サンプルのランダムウォークを実行したことになるので、1時間単位での変動率は毎回変わってきます。サンプル数が多くなれば変動率の確率は正規分布となり、実際の動きに近くなります。
ということで、pandasを使って1年分の1分足のインデックスを作ってみます。
idx = pd.date_range('2015/01/01', '2015/12/31 23:59', freq='T')
FX相場は週末は動かないので、idxのなかから平日の部分だけを取り出します。
weekidx = idx[idx.weekday<5]
次に、weekidxと同じサイズの$d(n)$を作成します。
dn = np.random.randint(2, size=len(weekidx))*2-1
ボラティリティは1年間の変動率なので、これを1分間の変動率に換算します。1年間の営業日数(260日とします)の1分足の総数の平方根で割って算出します。
Vola = 15.0 #ボラティリティ(%)
scale = Vola/100/np.sqrt(260*24*60)
gwalk = np.cumprod(np.exp(scale*dn))*p0
この1分足のランダムウォークをもとに、例えば4時間足のランダムウォークを作ってみます。
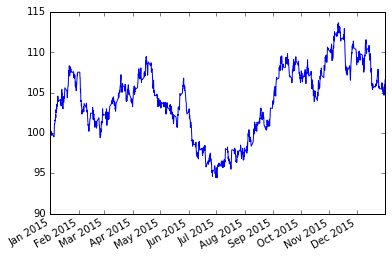
df = pd.Series(gwalk, index=weekidx).resample('4H').ohlc().dropna()
pandasのresample()メソッドを使って、4本値データを作成します。終値だけを表示させると次のようになります。
df['close'].plot()
これがボラティリティ15%のランダムウォークの一例です。といっても、ランダムウォークは毎回違うチャートになるので、合ってるかどうかはわかりませんが。