埋め込み層(Embedding Layer) : 文字データの数値化

0. 概要

この文章では、機械学習において文字や単語などの名義尺度を数値化するときに、次の3つにおいて何が違うのかを記述します。

1. 単純に通し番号等で番号付けしていく (例: a→97）
2. 総単語数の次元のベクトルを作る (例: a→[1,0,0], b→[0,1,0], c→[0,0,1])
3. 埋め込み層(Embedding layer)によって次数を圧縮したベクトルに写像する (例: a→[0.1,0.3], b→[-0.3,0.2], c→[0.9,-0.2])

通し番号はスカラー値なので1次元ベクトルに変換するともいえます。よってこの3つの違いは、単語を何次元の情報として扱うとよいかを問うものです。

また、(甘い + 酸っぱい) / 2 のように甘いと酸っぱいの間のような単語の演算ができることを目的としています。

結論です。

今回の例のデータとモデルの範囲内では、埋め込み層を用いた次元圧縮の方法がよい成績を収めています。単語数の次元の場合、過学習が起きていて、また通し番号の場合にはトレーニングデータでは学習がある程度できますが、単語の演算はできませんでした。

1. 文字を数値化する

a → 97, b → 98

個々の文字に数値を割り当てます。例えば、a は97、b は98のようにします。このようにして文字を数値化することによりコンピュータで文字を扱うことができるようになります。

97 + 98 ≠ ab

このときの97や98は、あくまでも文字を識別するための数値であって例えば97+98が ab というような演算はできません。

encoded(a)+encoded(b) ≒ ab

encodedは、文字や単語の数値化です。この記事では、この encoded の部分について、通し番号、総単語数次元のベクトル、次元圧縮したベクトルの3つの実装とその評価について記述します。

2. 問題設定

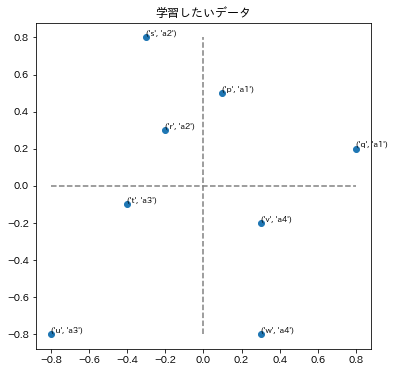
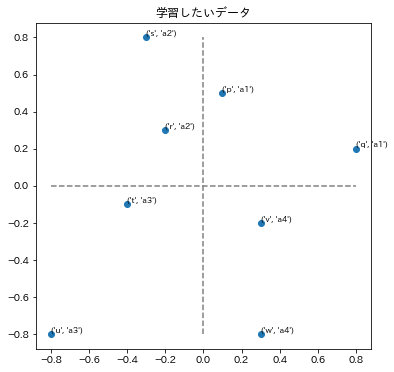
ポジショニングマップと呼ばれる2次元の位置情報と、その点が存在する領域名を学習することを目的とします。上の例の場合、各点の最初の文字が p ～ w まで名付けられたその点の名称、あとの a1 ～ a4 がその点が存在する領域を表す名前です。

ポジショニングマップとは、マーケティングなどの分野において例えば企業を分析するときに、規模や得意分野といった2つの指標を軸として各企業を2次元のマップ上に配置するものです。上の例の場合、 p ～ q までが各企業の名称に該当し、領域を表す a1 ～ a4 が例えば規模が大きく得意分野が〇〇といった領域ごとの特色を表す名前となります。

機械学習モデルでいうと次のような形になります。

文字(p～w) → 機械学習モデル → x座標,y座標,ラベル(a1,a2,a3,a4)

Question.1: 入力の文字から、ポジショニングマップの位置を求められるか？

まずはトレーニングデータの正解を復元できるかどうかを調べます。学習時の損失が十分に下がれば学習できたとします。

先に答えが知りたい方は、ここを開いてください。

(1) 通し番号、 (2) 総単語数次元のベクトル、(3) 次元圧縮(Embedding)のどれであってもある程度は実現できる。

Question.2: 点pと点qの間の点を、("p"+"q")/2で計算できるか？

入力データをそのまま記憶するような学習ではこの演算はできなく、入力文字からx,y座標を求め、そしてその座標に対して演算といった仕組みが機械学習モデルによって獲得される必要があります。

先に答えが知りたい方は、ここを開いてください。

(2)総単語数次元のベクトルと(3)次元圧縮(Embedding)である程度は実現できる。今回のデータとモデルでは(3)の方が成績が良い。(2)は過学習を起こしている。(1)は1次元に圧縮した入力の演算が2次元の位置を復元することは不可能で、学習することができていない。

3. 実行環境の準備

Google Colaboratoryを使用します。

準備

# 日本語matplotlibのインストール
!pip install japanize-matplotlib
import numpy as np
from numpy.random import seed
import tensorflow as tf
from tensorflow import keras
import matplotlib
import matplotlib.pyplot as plt
import japanize_matplotlib
import math

# 各種のバージョンを確認する
!python --version
print(f"numpy {np.__version__}")
print(f"tensorflow {tf.__version__}")
print(f"matplotlib {matplotlib.__version__}")

実行結果例

...(省略)...
Python 3.8.10
numpy 1.21.6
tensorflow 2.9.2
matplotlib 3.2.2

4. 学習用データの作成

学習用データの作成

# データを定義する。
poses0 = np.array([[0.1,0.5],[0.8,0.2],[-0.2,0.3],[-0.3,0.8],[-0.4,-0.1],[-0.8,-0.8],[0.3,-0.2],[0.3,-0.8]])
labels0 = ["a1","a1","a2","a2","a3","a3","a4","a4"]
names0 = ["p","q","r","s","t","u","v","w"]

# 位置pが第何象限にあるかを返す。戻り値は整数で0～3の数値で0は第1象限を表すとする。
def get_area(p):
  return int(((math.atan2(p[1],p[0])+2*math.pi)%(2*math.pi))//(math.pi/2))

# ポジショニングマップを表示する。
# values 座標値 np.ndarray [[x0,y0],[x1,y1],....]の形式
# labels 座標値のところに表示する文字列 len(labels)==len(values)の必要がある。
# colors 点の色 len(colors)==len(values)の必要がある。
# title グラフのタイトル
def plot_posmap(values,labels=[],colors=None,title=""):
  fig,ax = plt.subplots(facecolor="white",figsize=(6,6))
  ax.scatter(values[:,0],values[:,1],c=colors)
  ax.plot([min(*values[:,0]),max(*values[:,0])],[0,0],linestyle="dashed",color="grey")
  ax.plot([0,0],[min(*values[:,1]),max(*values[:,1])],linestyle="dashed",color="grey")
  for [x,y],l in zip(values,labels):
    ax.text(x,y+0.01,f"{l}",fontsize="small")
  ax.set_title(title)
  plt.show()

# 学習したいデータをポジショニングマップとして表示する。
plot_posmap(values=poses0,labels=zip(names0,labels0),title="学習したいデータ")

実行結果例

5. 各モデルを一般化する基底クラスの定義

各モデルを一般化する基底クラスの定義

from abc import ABC, abstractmethod

# このプロジェクトで扱うモデルを一般化する基底クラスの定義
class AbstractModel(ABC):

  # ここからはサブクラスでオーバーライドが必要な関数

  # 入力文字のエンコード
  @abstractmethod
  def str2num(self,x):
    pass
  # 評価用モデルの取得
  @abstractmethod
  def get_validation_model(self):
    pass
  # 学習用入力データの取得
  @abstractmethod
  def get_train_x(self):
    pass

  # ここからはサブクラスで共通して呼び出す関数

  # 学習用のモデルを取得する。  
  def get_training_model(self):
    return self.model
  # 学習のエポック数を取得する。
  def get_training_epochs(self):
    return self.learning_epochs
  # モデルの名称を取得する。
  def get_name(self):
    return self.model_name
  # 学習履歴をセットする。
  def set_learning_history(self,history):
    self.history = history
  # セットした学習履歴を取得する。
  def get_learning_history(self):
    return self.history

# モデルを保存する変数
models = []

このセルを実行したときの出力は特にありません。

Embeddingを使用するときにはトレーニング用と評価用のモデルを分けます。その理由は、"p"+"q"のような文字の演算の時、Embedding層からの出力を足し合わせて次の層に値を渡す必要があるため、トレーニングで作成したモデルをEmbedding層以降から使用します。このようにモデルの構造が変わるため、トレーニング用と評価用のモデルを分けています。一方、通し番号で数値化するモデル、総単語数の次元で数値化するモデルは評価モデルもトレーニングモデルも同じです。この違いを吸収するために基底クラスを作り、この基底クラスを派生する形で3つのモデルを実装します。

6. 通し番号による数値化

通し番号による数値化のモデル

class OneDimensional(AbstractModel):
  model = None
  model_name = "通し番号(1次元)"
  learning_epochs = 10000

  train_x = None
  inputs = None

  def __init__(self,inputs):
    self.inputs = inputs
    self.model = keras.models.Sequential([
        keras.layers.Input((1)),
        keras.layers.Dense(4,activation="tanh"),
        keras.layers.Dense(2+4), # x,yとラベル4つ
    ])
    self.model.compile(optimizer="adam",loss="mse")
    self.model.summary()

    # 0,1,2,3と順番に番号を振ります。
    # これを0-1の間に正規化すると学習が遅くなります。その理由は、
    # 中間層の活性化関数のtanhは入力が小さい時にはほぼ直線の形をしていて、
    # 非線形な関数を近似するためにtanhの値を大きくする必要があり、その
    # 大きくするというために学習時間を要します。
    self.train_x = np.array([[i] for i in range(len(self.inputs))]).tolist()
    # print(f"train_x:{self.train_x}")
  
  def get_train_x(self):
    return self.train_x
  def str2num(self,x):
    return np.array(self.inputs.index(x)).reshape((1,1))
  def get_validation_model(self):
    return self.model

models.append(OneDimensional(names0))

出力例

Model: "sequential_1"
_________________________________________________________________
 Layer (type)                Output Shape              Param #   
=================================================================
 dense_1 (Dense)             (None, 4)                 8         
                                                                 
 dense_2 (Dense)             (None, 6)                 30        
                                                                 
=================================================================
Total params: 38
Trainable params: 38
Non-trainable params: 0

---

入力層は1次元のベクトル、出力層はx座標、y座標の位置とa1～a4までの4つのラベルを識別する4つのニューロンです。この4つのニューロンのうち最も大きな値を示すニューロンの番号がどのラベルを予測したのかを表すことにします。例えば出力が 0.1,0.3, 0.2,-0.1,0.3,-0.6 ならば座標は(0.1,0.3)、ラベルはa3と解釈されます。

モデルは他のモデルと比較しやすいようにできるだけ余計なものはいれていません。ただ入力が1次元の場合、2次元の座標をそのまま計算することは不可能なので中間層としてニューロン数4の全結合レイヤーを入れています。

通し番号のつけ方の詳細

また入力値は0,1,2,3,...と番号を付けます。よく機械学習ではこの数値を0～1の間に正規化することがあるのですが、今回は行いません。その理由は、入力が小さい数字の場合には活性化関数のtanhの出力はほぼ直線になっていて非線形になる出力を近似するために入力を拡大する重みを作らないといけなくなるからです。その入力を拡大するところに多くの学習時間がかかってしまいます。

7. 総単語数次元のベクトル

総単語数次元に数値化するモデル

class MultiDimensional(AbstractModel):
  model = None
  model_name = "総単語数の次元"
  learning_epochs = 1000

  train_x = None
  inputs = None

  def __init__(self,inputs):
    self.inputs = inputs
    self.model = keras.models.Sequential([
        keras.layers.Input((len(self.inputs))),
        keras.layers.Dense(2+4), # x,y とラベル4つ
    ])
    self.model.compile(optimizer="adam",loss="mse")
    self.model.summary()

    # 学習、評価用の入力データ
    self.train_x = np.eye(len(self.inputs)).reshape((len(self.inputs),len(self.inputs))).tolist()
  
  def get_train_x(self):
    return self.train_x

  # 入力データを数値化する関数（モデルの学習後にこの関数は呼び出される）
  def str2num(self,x):
    return np.eye(len(self.inputs))[self.inputs.index(x)].reshape((1,len(self.inputs)))

  # 評価用モデルの取得
  def get_validation_model(self):
    return self.model

models.append(MultiDimensional(names0))

出力例

Model: "sequential_2"
_________________________________________________________________
 Layer (type)                Output Shape              Param #   
=================================================================
 dense_3 (Dense)             (None, 6)                 54        
                                                                 
=================================================================
Total params: 54
Trainable params: 54
Non-trainable params: 0
_________________________________________________________________

入力はone-hotと呼ばれる総単語数の次元で単語のあるところだけが1になるベクトルです。中間層はなく、出力層に直接接続します。

8. 次元圧縮(keras.layers.Embedding)

次元圧縮による数値化のモデル

class Embedding(AbstractModel):
  model = None
  model_name = "次元圧縮(Embedding)"
  learning_epochs = 2000

  train_x = None
  encoded_inputs = None
  validation_model = None
  inputs = None

  def __init__(self,inputs):
    self.inputs = inputs
    self.model = keras.models.Sequential([
      keras.layers.Input(shape=(1)),
      keras.layers.Embedding(input_dim=len(self.inputs),output_dim=2),
      keras.layers.Dense(2+4,use_bias=True), # x,y とラベル4つ
      keras.layers.Reshape((6,)),
    ])
    self.model.compile(optimizer="adam",loss="mse")
    self.model.summary()

    # 学習、評価用のデータ
    self.train_x = [[i] for i in range(len(self.inputs))]

  def get_train_x(self):
    return self.train_x

  # 入力データを数値化する関数（モデルの学習後にこの関数は呼び出される）
  def str2num(self,x):
    if self.encoded_inputs == None:
      # modelのembedding層の出力を得るためのモデルを作成する。
      embedding_model = keras.models.Model(inputs=self.model.input,outputs=self.model.layers[0].output)
      embedding_weights = np.array(embedding_model.predict([[i] for i in range(len(self.inputs))],verbose=0)).squeeze()

      # テキストとベクトルのセットを保存する。
      self.encoded_inputs = {k:embedding_weights[i].reshape((1,2)) for i,k in enumerate(self.inputs)}

    return self.encoded_inputs[x].reshape((1,1,2))

  # 評価用モデルの取得
  def get_validation_model(self):
    if self.validation_model == None:
      # 入力をテキストをベクトルに変換したそのベクトルの値、出力を画像とするモデルを作成する。
      self.validation_model = keras.models.Model(inputs=self.model.layers[1].input,outputs=self.model.output)
      # self.validation_model.summary()
    return self.validation_model

models.append(Embedding(names0))

出力例

Model: "sequential"
_________________________________________________________________
 Layer (type)                Output Shape              Param #   
=================================================================
 embedding (Embedding)       (None, 1, 2)              16        
                                                                 
 dense (Dense)               (None, 1, 6)              18        
                                                                 
 reshape (Reshape)           (None, 6)                 0         
                                                                 
=================================================================
Total params: 34
Trainable params: 34
Non-trainable params: 0
_________________________________________________________________

次元圧縮にはkeras.layers.Embeddingsを用います。このEmbeddingはまずone-hotの入力ベクトルを作成しその次に圧縮次元のレイヤーに全結合します。このレイヤーへのバイアスはありません。

9. モデルの学習

モデルの学習

for model in models:
  labels_set = sorted(set(labels0))
  labels_one_hot = np.eye(len(labels_set))
  train_x = model.get_train_x()
  train_y = [pos.tolist()+labels_one_hot[labels_set.index(labels0[i])].tolist() for i,pos in enumerate(poses0)]

  history = model.get_training_model().fit(train_x,train_y,epochs=model.get_training_epochs(),verbose=0,batch_size=1)
  print(f"{model.get_name()} last loss: {history.history['loss'][-1]}")
  model.set_learning_history(history)

出力例

次元圧縮(Embedding) last loss: 0.051758117973804474
通し番号(1次元) last loss: 0.022167451679706573
総単語数の次元 last loss: 3.790539437886764e-07

各モデルの操作は、基底クラスによって定義された関数を通して行われます。学習回数についても各モデルごとに損失が収束する時間が異なるため、各モデルのクラス定義の中で決められています。

10. 学習データの損失

学習データの損失の表示

# 学習の結果としてロスを描画する。ロスは小さくなるほど良い。
train_epochs = np.array(sorted(list(map(lambda x:x.get_training_epochs(),models)),reverse=True))

fix,axs = plt.subplots(ncols=2,facecolor="white",figsize=(9,5))
for i,mx in enumerate(train_epochs[:2]):
  for model in models:
    axs[i].plot(model.get_learning_history().history["loss"][:mx],label=model.get_name())
  axs[i].set_title("平均二乗誤差 (MSE)")
  axs[i].set_ylabel("loss")
  axs[i].set_xlabel("epochs")
  axs[i].legend()
plt.show()

出力例

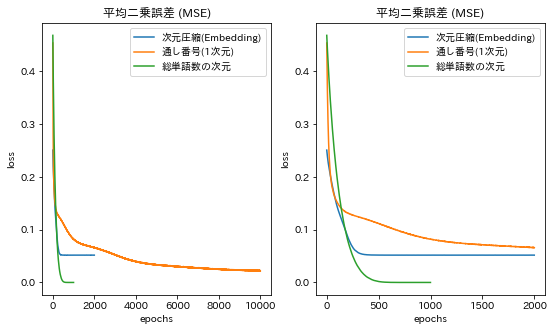
左はすべての損失値を描画し、右はその一部を拡大したものです。最終的に収束した損失では、次のような結果となっています。

総単語数の次元に数値化 < 通し番号で数値化 < 次元圧縮して数値化

学習時間は通し番号のモデルが長く、次元圧縮と総単語数は少しだけ次元圧縮の方が早く学習が収束しています。

11. 単語の演算結果

単語を演算した結果の表示

from itertools import combinations,product

fact_factories = []
for fi in range(5):
  fact_factories.append([])
  for i in range(fi,fi+1):
    c = combinations(names0,i+1)
    fact_factories[-1] += (fi+1,list(c))

# モデル名と[混合された入力の要素数,平均二乗誤差]
losses = {model.get_name():[[],[]] for model in models}

for [[fact_dim,fact_factory],model] in product(fact_factories,models):
  y_preds = []
  y_trues = []
  label_trues = []


  for fact_i,facts in enumerate(fact_factory):
    # 入力文字列のエンコードされた値を平均する。
    encoded = np.array(sum([model.str2num(fact) for fact in facts])) / len(facts)
    # print(f"encoded:{encoded}")

    # モデルで予測する。
    # print(f"validation model:{model.get_validation_model()}")
    y_preds.append(model.get_validation_model().predict(encoded,verbose=0)[0])

    # 正解データの作成
    pos_true = sum([poses0[names0.index(fact)] for fact in facts]) / len(facts)
    label_i_true = get_area(pos_true)
    label_trues.append(labels_set[label_i_true])
    y_trues.append(np.concatenate([pos_true,np.eye(4)[label_i_true]]))

  y_preds = np.array(y_preds)
  y_trues = np.array(y_trues)

  loss = tf.keras.losses.MeanSquaredError()(y_trues,y_preds).numpy()
  print(f"fact_dim:{fact_dim}, model:{model.get_name()}, loss:{loss}")
  losses[model.get_name()][0].append(fact_dim)
  losses[model.get_name()][1].append(loss)

  label_preds = np.apply_along_axis(func1d=lambda x:labels_set[np.argmax(x[2:])],axis=1,arr=y_preds)
  colors = list(map(lambda x:"blue" if x[0]==x[1] else "red",zip(label_trues,label_preds)))

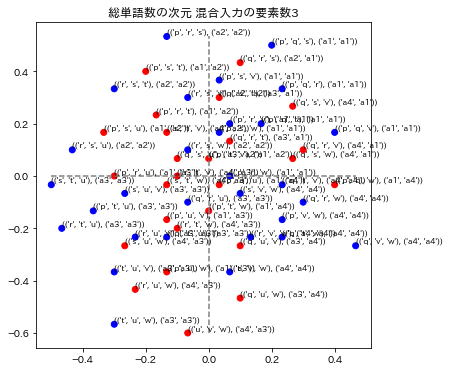
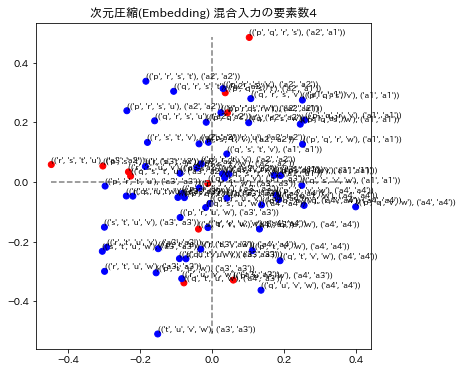
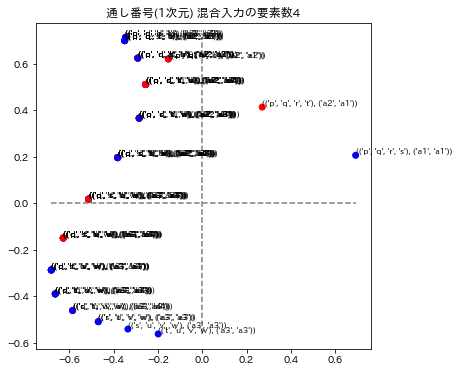
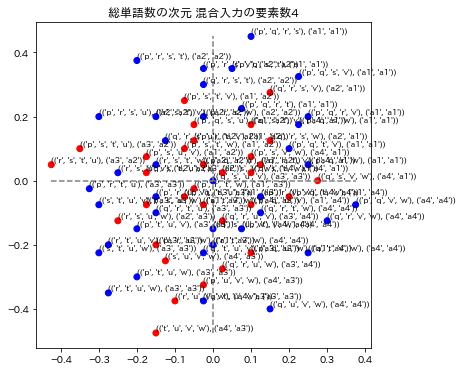
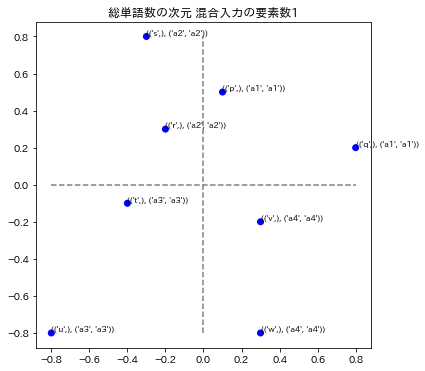
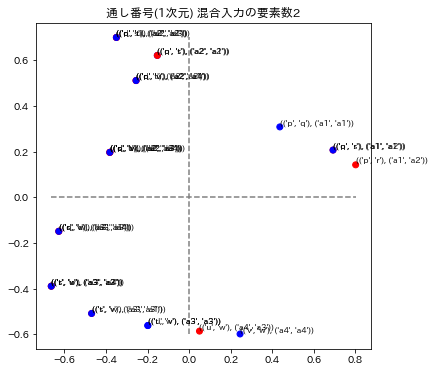
  plot_posmap(values=y_preds[:,:2],labels=zip(fact_factory,zip(label_preds,label_trues)),colors=colors,title=f"{model.get_name()} 混合入力の要素数{fact_dim}")

出力例

(以下省略 ...)

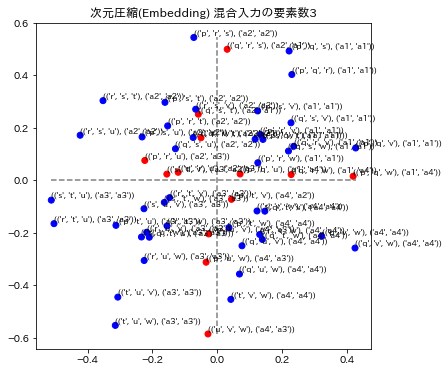
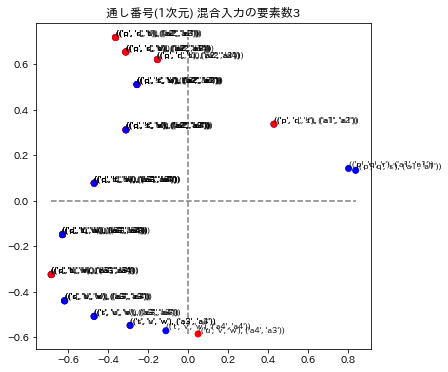
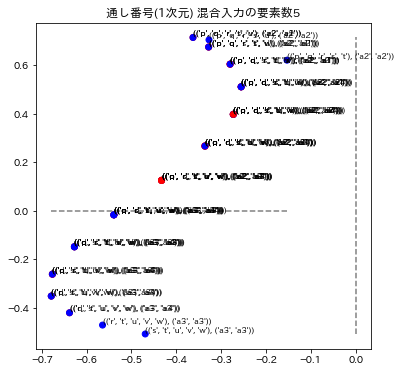
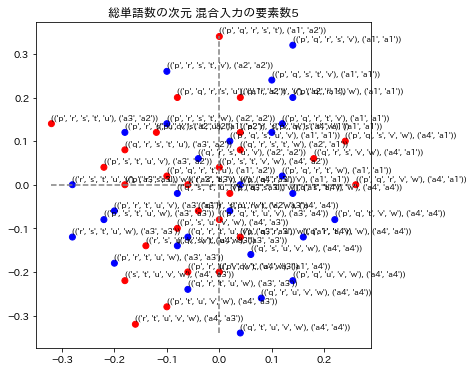
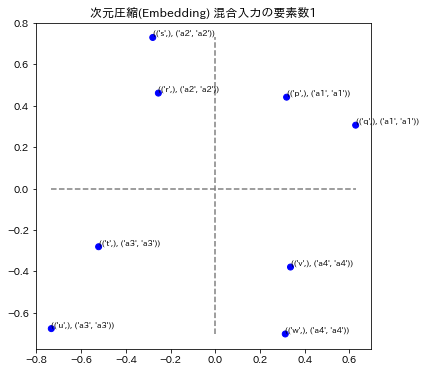
各グラフのタイトルは、次元圧縮、通し番号、総単語数の次元による数値化のモデル名称と、混合入力の要素数で表示されています。要素数とは、単語を演算したときの単語数です。例えば ("p"+"q"+"r")/3を計算したときは要素数3としています。

3モデルの演算の要素数1と2を表示しています。要素数1の場合はトレーニングデータを再現できているかどうかに相当します。図の青い点はa1～a4のラベルが正解してる場合で、赤い点はそのラベルが不正解になっています。x,y座標の誤差はこの図では表されていません。

省略したグラフ

12. 評価

それぞれのモデルの損失の表示

# 混合された入力の要素数と損失
fig,ax = plt.subplots()

for name in losses.keys():
  ax.plot(losses[name][0],losses[name][1],label=name)
ax.set_title("モデルごとの混合された入力の要素数とその予測値の平均二乗誤差")
ax.set_xlabel("混合された入力の要素数")
ax.set_ylabel("平均二乗誤差")
ax.set_xticks(list(losses.values())[0][0])
ax.legend()
plt.show()

出力例

先ほどの単語の演算を行ったときに記録した損失を表示しています。損失は小さいほど、良いです。グラフの横軸は演算に使用した単語の数で縦軸が損失です。要素数1の場合は、トレーニングデータそのものです。要素数2以降はトレーニングデータには無いデータを評価していることになります。

要素数1を見ると、次元圧縮は通し番号と総単語数よりも悪い結果となっています。しかし要素数2以降では一番良い成績を収めています。これは、次元を圧縮することによってモデルはまずx軸とy軸の数値を求め、そこから象限であるラベルを求めていることが他のモデルよりも少しできていることになります。言い換えると、総単語数の次元による数値化の場合は、入力データから直接ラベルを求めていることが少しあるともいえます。

ただこの結果はモデルを少し変更すると変わることがあります。例えば次元圧縮に中間層を追加すると過学習を起こしたり、または総単語数の次元にもニューロン数を少なくした中間層を入れるとそこで次元圧縮が行われてよい成績となることがあります。

13. まとめ

今回の例は入力の総数単語数が8と小さかったため、Embeddingによる次元圧縮の効果は少しだけのものとなりました。ただ一方、言語データのように現実的なデータの場合には膨大な大きさの総単語数になるため、おそらくEmbeddingの効果がしっかりと現れるのだと思われます。