0. 概要
- 本記事は、畳み込みニューラルネットワーク(CNN)を学ぶためのものです。
- 題材としてあえて画像分類ではなく五目並べの勝利判定を扱います。
- その理由は、画像だとネットにあるサンプルで何となく分類に成功してしまい畳み込みニューラルネットワークが何をしているのかいまいち理解できないからです。
- 五目並べはマスの目になった盤面に自分の駒が縦横斜めのどれか1つで5個並んだ状態になったら勝利するというゲームです。
- CNNに期待することは、盤面の状態とどちらのプレイヤが勝利したか、または引き分けかの情報だけを与えて、勝利判定のルールを自動で導き出すことです。
1. 畳み込みニューラルネットワークとは
入力データを画像とすると、画像に小さいサイズのフィルタを何枚か適用しその結果から画像に映っているものを判定したりするものです。このフィルタは人が与えるのではなく、学習データから自動的に導き出されます。
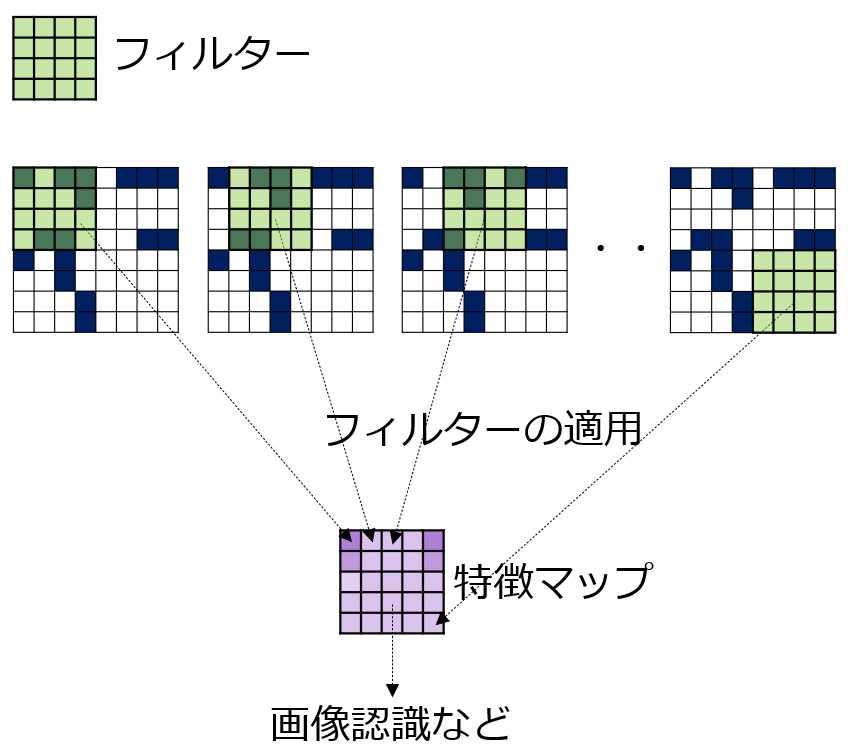
↑の例は1つのフィルタを画像に適用している例です。フィルターを画像の左上から順番に適用し、その結果が特徴マップと呼ばれる二次元マップで得られます。画像認識などの判定は、この特徴マップを使って行われます。実際には、フィルターは1枚ではなく複数枚を利用したり、大きさを変えて何度も実行したりします。
畳み込みニューラルネットワークは、英語名称でConvolutional Neural Network、CNNと略されたりします。
2. 五目並べの勝利判定
畳み込みニューラルネットワークは、画像を認識したり分類するのによく利用されます。しかし本記事では画像の場合にはデータが複雑になりすぎてCNNの機能について理解することは少し困難になります。そこで、五目並べの勝利判定を題材とします。
五目並べとは、マス状になった盤面に2人のプレイヤが交互に自分自身の駒を置き、駒が縦、横、斜めに5つ連続すると勝ちとなるゲームです。
五目並べの勝利判定とは、ある盤面を見たときにどちらのプレイヤが勝利しているのか、またはまだ決着していないのかを判定することです。
この記事では、盤面サイズの関係上、4つの駒が連続すると勝ちとします。四目並べともいえるわけですが四目並べは少し違う別のゲームを表すこともあるので五目並べで勝利条件は4コマ連続という説明にしています。

↑ 青はプレイヤ1、オレンジはプレイヤ-1の駒で、プレイヤ1が勝利している盤面です。本記事では、縦横斜めのいずれかで4つ連続すると勝利としています。
3. プログラムの実行環境
Google Colaboratoryを使用します。また盤面の表示は、IPythonを通して javascript によって実現します。
ここからは実際にプログラムを提示しながら説明していきます。
4. 盤面の表示関数、盤面のサイズと勝利条件の定義
import IPython
import random
import copy
import uuid
# 盤面のサイズ
board_size = 8
# コマ数の勝利条件
happy_end = 4
# 盤面を表示する関数
def print_cells(c):
c_sz = 20
def fs(x): return {1:"darkblue",-1:"darkorange",0:"gainsboro"}[x]
uid = f"canvas_{str(uuid.uuid1())}"
html = f"<canvas id='{uid}' width='{c_sz*board_size}px' height='{c_sz*(board_size+1)}px'></canvas>"
display(IPython.display.HTML(html))
fs0 = "[{0}]".format(",".join(list(map(lambda x:str([x,fs(x)]),[1,-1,0]))))
fs1 = "[{0}]".format(",".join(list(map(lambda x:f"'{fs(x)}'",c))))
javascript = ('''
fs0={1};fs1={2};canvas=document.querySelector("#{4}");ctx=canvas.getContext("2d");
for(let i=0;i<3;i+=1){{ctx.fillStyle=fs0[i][1];ctx.fillRect(2*i*{3},0,{3}-2,{3}-2);ctx.fillText(fs0[i][0],(2*i+1)*{3},16);}}
for(let y=0;y<{0};y++){{ for(let x=0;x<{0};x++){{ctx.fillStyle=fs1[y*{0}+x];ctx.fillRect(x*{3},(y+1)*{3}+2,{3}-2,{3}-2);}}}}
''').format(board_size,fs0,fs1,c_sz,uid)
display(IPython.display.Javascript(javascript))
# print_cells関数の動作確認
cells = [0,0,0,0,0,0,0,0, 1,1,0,1,1,1,0,0, 1,0,-1,-1,0,-1,0,0, 0,1,-1,0,1,-1,0,0, 0,0,1,1,-1,-1,0,0, 0,0,0,1,1,1,0,0, 0,0,0,0,0,0,0,0, 0,0,0,0,0,0,0,0]
print(f"size cells:{len(cells)}")
print_cells(cells)
出力例
盤面の1辺のマス数を board_size, 何個連続すれば勝ちなのかの勝利条件を happy_end 変数で作成しています。
5. 正解データを作るための勝利判定関数
# 横縦斜めの勝利判定
def judge(c):
# 盤面の縦軸の値と不整合な横軸の値(例えば0行目の横軸の値が0~board_size-1の範囲外なら不整合)と、盤面の外側にある盤面リストのインデックスを-1に補正する。
def idx_norm(i,y): return -1 if i>=board_size**2 or i//board_size!=y else i
# 縦方向の勝利判定ラインのインデックス取得
def idx_wh(x,y): return idx_norm(y*board_size+x,y)
# 横方向の勝利判定ラインのインデックス取得
def idx_hw(x,y): return idx_wh(y,x)
# 右下がり斜め勝利判定ラインのインデックス取得
def idx_rd(x,y): return idx_norm(x+y*board_size+(happy_end-board_size)+y,y)
# 左下がり斜め勝利判定ラインのインデックス取得
def idx_ld(x,y): return idx_norm(x+y*board_size+(happy_end-1)-y,y)
# インデックス-1のときに 0 を返す盤面リストからの状態取得
def v(c,i): return 0 if i<0 else c[i]
# 横軸方向に処理を繰り返す。
for x in range(max(2*board_size-1-2*(happy_end-1),board_size)):
# 勝利判定を行うラインのインデックスを求める関数を用意する。ただしそのラインで勝利できるだけのマスが存在しないラインの関数は作らない。
idxes_funcs = ([idx_wh,idx_hw] if x<board_size else []) + ([idx_rd,idx_ld] if x<(2*board_size-1)-2*(happy_end-1) else [])
# 連続するプレイヤの駒数を保存する変数を0で初期化する。
counts = players = [0 for i in range(len(idxes_funcs))]
# 縦軸方向に処理を繰り返す。
for y in range(board_size):
# x,yから勝利判定ラインの盤面リストの該当するインデックスを取得する。
idxes = list(map(lambda f:f(x,y),idxes_funcs))
# 連続駒数を必要に応じてインクリメントする。
counts = list(map(lambda i:counts[i[0]]+1 if players[i[0]]!=0 and players[i[0]]==v(c,i[1]) else 1,enumerate(idxes)))
# 連続駒をカウントしたプレイヤ番号を保存する。
players = list(map(lambda i:v(c,i),idxes))
# 勝敗判定ラインのどれかが勝利条件の駒数に達した場合を確認する。
if max(counts)==happy_end:
# 勝利条件に到達したプレイヤ番号を返す。
return players[counts.index(happy_end)]
# 勝利者なしとして関数を終了する。
return 0
この記事の目的は、CNNによって五目並べの勝利判定をすることです。そのモデルの学習用データは、盤面とその盤面での勝利者、または引き分けを持つデータとなります。この勝利者または引き分けを正しく判定する関数を予め作成しておきます。
CNNはこの勝利判定関数をデータから作り出す、ということもできます。
この関数の説明は、本記事の目的とは異なりますので省略いたします。
6. モデル学習用データの作成
盤面の状態を表すには、モノクロ画像と同じように 横×縦 のリストがあれば十分です。

[[ 0 -1 1 1]
[ 0 1 0 -1]
[ 1 -1 0 -1]
[-1 1 1 0]]
↑ 上の盤面を2次元配列で表す例です。この場合、入力データの形状は、(4,4)となります。
この記事のあとに記載されている失敗例で詳しく述べるのですが、この形状の入力データだとモデルはなかなか学習できません。その理由は、1つにはプレイヤ1の勝利判定を行う時にプレイヤ-1の駒も計算に入れようとしてしまうからです。
盤面にプレイヤごとの次元が増えたので、これで入力データの形状は (4,4,2)となります。最後の2は2名のプレイヤという意味です。
そして最後に3次元になった盤面情報にCNNを適用するために形状を合わせて (4,4,2,1) とします。最後の1は、モノクロ画像のようにチャネル数1を表します。
まとめると、入力データの形状は(盤面の横, 盤面の縦, 2, 1)となります。
出力は、プレイヤ1、プレイヤ-1、引き分けの3パターンを確率的に得たいためone-hotと呼ばれる1つの要素だけが1であるベクトルで表します。よって出力データの形状は(3)です。
以下にこれらの形状に変換するコードを含んだ学習用データ作成プログラムを示します。
import numpy as np
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers
# AIの学習用データの個数
data_num = 1000
# 表示用形式から学習用形式に盤面情報を変換する。
def encode_x(x):
assert isinstance(x,list) or isinstance(x,np.ndarray)
# -1, 1の one hot vectorを作成する。
def onehot2(x):
return [1 if i==x else 0 for i in range(-1,2,2)]
# バッチ形式の場合
if isinstance(x[0],list):
return np.array(list(map(onehot2,np.array(x).flatten()))).reshape((len(x),board_size,board_size,2,-1))
# 単独のインスタンスの場合
return np.array([*map(onehot2,x)]).reshape((board_size,board_size,2,-1))
# 学習用形式から表示できる形式へ入力データを変換する。
def decode_x(x):
return np.apply_along_axis(func1d=lambda v:0 if 1 not in v else v.tolist().index(1)*2-1,axis=-1,arr=np.squeeze(x)).flatten()
def build_data(data_num):
# -1,0,1のone hot vectorを作成する。
def onehot3(x):
return [1 if i==x else 0 for i in range(-1,2)]
# ランダムに手を打って勝者が決まる、または手が無くなるまで盤面を繰り返してトレーニングデータを作成する。
train_x = []
train_y = []
turn_n = 36 # 何手打つか
for _ in range(data_num):
cells = [0 for _ in range(board_size**2)]
winner = 0
indices = random.sample([i for i in range(board_size**2)],board_size**2)
for i,idx in enumerate(indices[:turn_n]):
cells[idx] = -1 if i%2==0 else 1
winner = judge(cells)
if winner != 0:
break
train_x.append(cells)
train_y.append(winner)
print("勝者の個数")
for p in range(-1,2):
print(f"{'引き分け' if p==0 else p} : {(np.array(train_y)==p).sum()}")
# データの変形
# train_x, train_yともにonehot形式とする。
train_x = encode_x(train_x)
train_y = np.array([*map(onehot3,train_y)])
return train_x,train_y
# データの生成
train_x,train_y = build_data(data_num=data_num)
print(f"train_x:{train_x.shape}, train_y:{train_y.shape}")
# データを1つ取り出して検証する
sample_idx = random.randint(0,train_x.shape[0]-1)
print(f"sample data index:{sample_idx}")
print_cells(decode_x(train_x[sample_idx]))
print(f"winner([-1の勝利,引き分け,+1の勝利]):{train_y[sample_idx]}")
出力例(乱数を使用しているので実行ごとに変わります)
勝者の個数
-1 : 305
引き分け : 355
1 : 340
train_x:(1000, 8, 8, 2, 1), train_y:(1000, 3)
sample data index:412
winner([-1の勝利,引き分け,+1の勝利]):[1 0 0]
データは1000個作成します。ランダムに盤面を作り、プレイヤ-1、プレイヤ1のどちらが勝利したか、または引き分けかをデータとして保持します。
出力例では、1000個の盤面の勝者ごとの盤面数、入出力データの形状、そして1000個のうち1つを取り出して盤面の状態で表示しています。
7. CNNを用いた機械学習モデルの作成
プレイヤごとに分けた盤面からどちらのプレイヤが勝利しているか、または引き分けかを判定するモデルの概要を以下に示します。

CNNのフィルタは本記事における勝利判定の連続コマ数である 4 のサイズとします。4個の連続する駒を見つけるためには、このフィルタで抽出した4x4の盤面があれば十分だからです。
次にフィルタから抽出された値をマップにした特徴マップでは、勝利条件を充たしているとフィルタが判断した個所は値が大きくなっていると想定されます。そして勝利条件は1カ所でも4コマ連続があれば良いので、この特徴マップの最大値のみが重要になってきます。そこで特徴マップの最大値を取り出します。
同様に別のプレイヤの盤面からも特徴マップの最大値を取り出し、この2つの値でどちらのプレイヤが勝利しているか、またはどちらも勝利していないかを判定します。
最後の部分は入力が2、出力が3の全結合層のニューラルネットワークで実現します。以下にそのコードを示します。
inputs = layers.Input(shape=train_x.shape[1:])
x = inputs
x = layers.Conv3D(
filters=12, # 縦,横,右下斜め,右上斜めの最低で4つのフィルターが必要
kernel_size=(happy_end,happy_end,1), # 勝利判定の最小サイズ
padding="same", # 0パッドの枠を追加して盤面の端が必ずフィルターの端になるという現象を回避する。
kernel_constraint=keras.constraints.non_neg(), # マイナスの掛け算でたまたま答えを導く計算式を見つけないようにする。
use_bias=False # バイアスでたまたま答えを導き出すと過学習になるのでそれを回避するため。
)(x)
x = layers.Permute((1,2,4,3))(x)
x = layers.GlobalMaxPool3D()(x)
x = layers.Dense(train_y.shape[-1],activation="softmax")(x)
model = keras.models.Model(inputs=inputs,outputs=x)
model.compile(optimizer="adam",loss="categorical_crossentropy",metrics=['accuracy'])
model.summary()
出力例
Model: "model_3"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
input_4 (InputLayer) [(None, 8, 8, 2, 1)] 0
conv3d_3 (Conv3D) (None, 8, 8, 2, 12) 192
permute_3 (Permute) (None, 8, 8, 12, 2) 0
global_max_pooling3d_3 (Glo (None, 2) 0
balMaxPooling3D)
dense_3 (Dense) (None, 3) 9
=================================================================
Total params: 201
Trainable params: 201
Non-trainable params: 0
_________________________________________________________________
3次元のCNNからの出力は、(盤面の横, 盤面の縦, プレイヤの次元, フィルタ数)の形状となっているのでプレイヤごとの特徴マップの最大値をGlobalMaxPooling3Dレイヤで得るために次元を(盤面の横, 盤面の縦, フィルタ数, プレイヤの次元)とPermuteレイヤを使って変えています。
GlobalMaxPooling3Dレイヤの出力はプレイヤごとの特徴マップの最大値です。これを入力として3要素の出力を全結合層で行います。この3要素は、プレイヤ-1の勝利確率、引き分けの確率、プレイヤ1の勝利確率となっています。
8. モデルの学習
print(f"train_x:{train_x.shape}, train_y:{train_y.shape}")
history = model.fit(train_x,train_y,epochs=1000,batch_size=64)
出力の一部の例
...
Epoch 1000/1000
16/16 [==============================] - 0s 19ms/step - loss: 0.0043 - accuracy: 1.0000
1000回の学習を実行します。バッチサイズは64に、デフォルトの32から変更していますが特に大きな意味はありません。
学習は loss(損失) が、この例の 0.0043 のような値にならないことがあります。例えば 0.05 ぐらいでそれ以降下がらないことがあります。この原因はおそらくフィルター数の問題です。今回のモデルではフィルター数を12としていますが、このフィルターは同じ答えを2つ以上のフィルターが追ってしまうと他のまだどのフィルターもたどり着いていない正解をどのフィルタも獲得することができなくなってしまうからです。もしも損失が 0.01未満にならない場合は、モデルを作り直してフィルターの重みを再度初期化したり、フィルター数を増やして実行してみてください。
9. 学習過程の損失と分類精度の描画
学習時にhistory変数に保存した損失と正確に分類できた率を描画します。
import matplotlib.pyplot as plt
# 描画領域を作成します。
fig,axs = plt.subplots(ncols=2,figsize=(12,4),facecolor="white")
for i,tp in enumerate(["loss","accuracy"]):
axs[i].plot(history.history[tp])
# タイトル、x軸y軸のラベルを設定します。
axs[i].set_title(tp)
axs[i].set_xlabel("epochs")
axs[i].set_ylabel("loss")
plt.show()
出力例
10. モデルの評価
先に示した分類率は、トレーニングデータにおける分類率です。ここで100%となっていてもモデルが五目並べの勝利判定をちゃんと理解したとはいえません。それは、トレーニングデータにはない未知の盤面でも同様に正確に分類できるかどうかを確かめていないからです。
# 評価
test_x,test_y = build_data(100)
model.evaluate(test_x,test_y)
出力例
勝者の個数
-1 : 28
引き分け : 35
1 : 37
4/4 [==============================] - 0s 8ms/step - loss: 0.0043 - accuracy: 1.0000
[0.004322880879044533, 1.0]
上記のコードによって新しい盤面を100個作成します。そしてモデルを評価します。出力例の accuracy が分類率です。トレーニングデータには無かった未知のデータでも100%分類できていることが分かります。
11. フィルターの可視化
フィルターは、縦横斜めの連続する駒を見つけるように設計されました。この意図どおりにフィルターが学習データから自動的に導き出されているかを確認します。
# カーネルの重みのフィルタ
# いわゆるフィルタの値を可視化する。学習後に重みが決定される。
# 特徴ベクトルとことなり可視化時に入力データには依存しないので、可視化にデータはは不要である。
import matplotlib.pyplot as plt
import math
# weightsはlist、weightsの0はカーネル、1はバイアスのnp.array
weights = model.layers[1].weights[0]
mx = max(weights.numpy().flatten())
mi = min(weights.numpy().flatten())
nor_weights = (weights - mi) / (mx - mi)
n_k = weights.shape[-1]
ncols = min(8,n_k)
fig,axs = plt.subplots(facecolor="white",figsize=(16,4),nrows=math.ceil(n_k/ncols),ncols=ncols)
if len(axs.shape)==1:
axs = axs.reshape((1,axs.shape[0]))
for k in range(n_k):
# mx = max(nor_weights[:,:,0,0,k].numpy().flatten())
# mi = min(nor_weights[:,:,0,0,k].numpy().flatten())
axs[k//ncols,k%ncols].imshow(nor_weights[:,:,0,0,k],vmax=1,vmin=0)
# 描画していない領域のクリア
for col in range(k%ncols+1,ncols):
axs[-1,col].axis("off")
plt.show()
出力例
12個のフィルターが表示されています。この図は、数値の大きなところが明るい色で描画されるようになっています。また数値は12個のフィルター全体を通して0から1の間に正規化されていますので、フィルターによってはどこ数値も大きくないというものが現れます。
可視化されたフィルターを見ると、縦横斜めのものがそれぞれ現れていることが分かります。縦と横は位置を変えて2種類のフィルターが作られていますがこれは冗長でどちらか1つでも同様の結果が得られると考えられます。

つまりこのAIモデルは、フィルターを通過したプレイヤ1または―1の駒の数を数えています。このような勝利条件のルールをAIが見つけているともいえます。
12. 特徴マップの可視化
特徴マップは、入力データをフィルターを通して得られた二次元マップです。ここでは盤面の端に作られた縦の連続コマの盤面とランダムに作られた盤面の特徴マップを描画します。
# カーネルを通したあとの入力データの可視化
# 入力データの特徴ベクトルを可視化するということ
import math
# 特徴マップを出力するための機械学習モデル
model_feature = keras.models.Model(inputs=model.input,outputs=model.layers[1].output)
# 0列目は-1、最後の列は1のプレイヤの駒を置く。
col2player = {0:-1,board_size-1:1}
sample_x = [col2player.setdefault(i%board_size,0) if i//board_size<4 else 0 for i in range(board_size**2)]
# print(f"judge: {judge(sample_x)}")
# ランダムにデータを2つ作成する。
test_x,_ = build_data(2)
test_x = np.append(encode_x(sample_x)[np.newaxis],test_x,axis=0)
for i in range(len(test_x)):
x = test_x[[i]]
decoded_x = decode_x(x)
print_cells(decoded_x)
sample_y = model.predict(x,verbose=0)
features = model_feature.predict(x,verbose=0)
print(f"予測された勝利者:{np.argmax(sample_y)-1}, 真の勝利者:{judge(decoded_x)}")
print(f"[-1の勝利,引き分け,+1の勝利]の確率:{sample_y}")
n_features = features.shape[-1]
ncols = min(8,n_features)
for p in range(2):
fig,axs = plt.subplots(facecolor="white",figsize=(12,4),nrows=math.ceil(n_features/ncols),ncols=ncols)
if len(axs.shape)==1:
axs = axs.reshape((1,axs.shape[0]))
values = features[0,:,:,p,:]
mx,mi = max(values.flatten()),min(values.flatten())
nor_features = (values - mi) / (mx - mi)
# print(f"-- {nor_features.shape}")
for feature_i in range(n_features):
axs[feature_i//ncols,feature_i%ncols].imshow(nor_features[:,:,feature_i],vmax=1,vmin=0)
plt.show()
出力例
予測された勝利者:0, 真の勝利者:-1
[-1の勝利,引き分け,+1の勝利]の確率:[[2.5534204e-03 9.9681705e-01 6.2961731e-04]]
予測された勝利者:1, 真の勝利者:1
[-1の勝利,引き分け,+1の勝利]の確率:[[4.7490040e-11 2.9111204e-03 9.9708885e-01]]
出力は、盤面の下にオレンジのプレイヤ-1の特徴マップ、次に青のプレイヤ1の特徴マップが表示されています。特徴マップは、12個のフィルターを通して作られた二次元マップなので、各フィルターに対応する12個のマップが表示されています。
1つ目の盤面の上部に縦の列が作られた盤面の特徴マップを確認すると、プレイヤ-1は6番目のフィルタで勝利条件が求められ、プレイヤ1では2番目のフィルタが使われていることが分かります。これは縦ラインのフィルタがフィルタの端にラインを作ってしまったためです。端ではなくフィルタの中央部分にラインを作ることができていれば、1つのフィルタでどちらも判定できるようになります。このような現象は、フィルタの重みの初期値によって変わるので、次に実行したときにはまた異なる結果が表示されると考えられます。
2つ目の盤面は青のプレイヤ1が勝利しているわけですが、右上に横の4つの駒がありそこが決め手になっているはずです。横のラインを作っているフィルタは5番目と10番目です。プレイヤ1の特徴マップでも黄色く示されているところは5番目と10番目です。この値が決め手になっていることが伺えます。
13. フィルターの最小数とパディング
パディング(padding)とは畳み込みニューラルネットワークのパラメータの1つで、"same"または"vallid"を指定します。すでに示したモデルの例ではsameを使用していました。

↑の例は(8,8)の盤面に(4,4)のフィルタを適用するときのpadding=validとsameの違いです。validの場合は盤面を拡張せずに端からフィルターを適用していきます。一方sameの場合は、盤面を少し広げてからフィルターを適用していきます。なぜ広げるかというと1つは特徴マップが元の盤面のサイズと同じになるからです。この同じという意味でpadding=sameというパラメータの設定になります。
勝利判定を考えた場合、盤面の端に4つの駒が並ぶ場合にpadding=validの場合には左端に4個が並ぶ場合と右端に4個が並ぶ場合を判定するために別のフィルターが必要になります。これが駒が横と縦に並ぶ2パターンあるので必要なフィルター数の最低数は6個です。
一方padding=sameの場合には外に枠が作られるので、またその枠は0で埋められて駒がない状態になるので、フィルターの中央で縦や横のラインを作れば左端でも右端でも同じフィルターで判定することができるようになります。よって必要なフィルター数は4つとなります。
14. モデルが勝利判定をできないという失敗例
ここではモデルが勝利判定を自動で導けないケースについて記述します。
14.1. 上記の成功例と同じモデルのパラメータで失敗する場合
12個のフィルターとしていますが、縦、横、右下がりの斜め、右上がりの斜めの4つの勝利条件を見つけられなかった場合に失敗します。見つけられなかったとは、複数のフィルタが同じ条件を追ってしまった場合です。フィルタは損失を減らす方向にしか変化できないので、最初に見つけた勝利条件のパターンにしか向かっていけないという特徴があります。
また以下のように斜めの勝利条件をずらして学習してしまうケースもあります。ここに入り込むとこのフィルタは正解のパターを得ることはできません。

14.2. フィルター数が少ない場合
上記の複数のフィルターで同じパターンを追ってしまうケースが発生したときに、見つけられないパターンを作ってしまう確率が上がります。
以下はフィルター数4で実行した例です。結果はその都度変わります。
Epoch 1000/1000
16/16 [==============================] - 0s 10ms/step - loss: 0.6069 - accuracy: 0.7750
1000回の学習後の損失は0.6069とだいぶ高くなっています。このときのフィルターを見ると次のようになっています。

縦ラインは正解を得ようとしています。横ラインは一見良いのですけど、padding=sameとしているため盤面の下端に横に駒が連続する場合の勝利判定ができません。また2番目3番目のフィルターは恐らく横や縦のラインを追いつつ斜めの勝利データにも引っ張られて値が落ち着いていないと考えられます。
フィルタ数を理論上最小の4に設定しても学習できるときはあります。ただ失敗することも多いので今回のデータでは3倍の12と設定しました。ただこれでもたまに失敗することがあります。
14.3. Conv3Dのバイアスを使う場合
今回のモデルではConv3Dの引数に use_bias=False を指定してバイアスを不使用にしています。ここをデフォルトのTrueにして実行すると学習に時間がかかったり、トレーニングデータでは学習できてもテストデータで分類精度が低いことがあります。その理由は、バイアスによって1つのニューロンが負の数や不必要に大きな値を出力することができるようになってしまうからと考えられます。バイアスは、ニューロンの活性化関数の出力を左右に移動させることができ、Conv3Dのデフォルトの活性化関数である線形関数を左右に移動させると負の数や不要に大きな値を出力できます。こうすると、1つの駒で勝利が決定してしまったり、また連続していない関係のない駒が負の値を出力して相手を勝利させたりもできるようになってしまいます。
このようにしてたまたまトレーニングデータで勝利判定ができてしまったフィルターをAIは作ってしまうことがあり、しかしそのようなフィルターはテストデータでは通用しないためAIの学習としては成功しません。
例えばバイアスを入れて学習すると次のような結果になります。結果は実行するごとに変わります。この例は、上手くバイアスの機能を表してくれた例で、いつもこのような結果が出るわけではありません。
Epoch 1000/1000
16/16 [==============================] - 0s 14ms/step - loss: 0.0355 - accuracy: 1.0000
損失(loss)は0.0355と少し大きいのですが、分類率(accuracy)は1.0となっています。
次にテストデータで評価した結果は次のようになります。
4/4 [==============================] - 0s 8ms/step - loss: 0.0834 - accuracy: 0.9900
[0.08339731395244598, 0.9900000095367432]
何度か実行していくと分類に失敗するデータがあります。これを描画してみます。
[-1の勝利,引き分け,1の勝利]:[[9.9263215e-01 7.3675807e-03 3.9252299e-07]], 真の勝利:0
モデルはプレイヤ-1の勝利と判定した盤面です。しかし真の勝利判定は引き分けです。ここから考えられることは、プレイヤ-1が勝利した盤面からモデルは過度にその特徴を学んでしまったということです。その特徴がこの盤面にもあってプレイヤ-1の勝利と判定してしまった可能性があります。
この実行時のフィルターを描画すると次のようになりました。
14.4. フィルターの重み計算に制限を付けない場合
今回のモデルではConv3Dの引数に kernel_constraint=keras.constraints.non_neg() を指定して重みには負の数を使用しないという制限をつけています。これをつけない場合、実行するのに時間がかかったり学習できないことがあります。その理由は不要な計算がモデルの学習を阻害するからと考えられます。
五目並べの勝利判定は、自分の駒は自分の勝利確率を”上げる”だけで、例えばあるマスに駒を置くと勝利確率が下がるということはありません。ここでいう勝利確率は、相手は関係なく単純に自分が勝つ確率と考えてください。そのような確率は駒を置くごとに単純増加して減ることはありません。
しかしフィルタの重みに負の値が許容されると、駒が勝利確率を下げることができるようになります。計算はより複雑になり、例えば真の回答からは遠ざかるのですけど負の重みを使って一時的に損失を減らすことが可能になります。そのような正解ではないのですけど損失のくぼみのようなところをローカルミニマムと呼びます。すべてのフィルタがローカルミニマムに入ってしまうとモデルの学習はそれ以降先に進みません。
以下は、負の重みを許容した場合の学習例です。実行結果は実行ごとに変わるので、あくまでも一例です。
...
Epoch 2000/2000
16/16 [==============================] - 0s 17ms/step - loss: 0.8713 - accuracy: 0.5840
実行は学習に成功した例の倍の2000回を行っています。しかし損失は下がっていません。
このようなことが起こらないように、負の重みを制限しすべての駒は勝利判定においてプラスに働くという制限下でモデルを学習させます。言い換えると負の重みを使って計算して少しだけ損失は下げる、でも真の回答からは遠ざかるようなローカルミニマムを抑えているともいえます。
14.5. プレイヤごとの盤面を分けない、または駒がない盤面も使う場合
画像認識で用いるCNNは、Conv2Dを使用します。ここでの五目並べの勝利判定についても画像認識のようにConv2DでAIを作成すると、↑の「画像と解釈 8×8×2チャネル」のようになり、この場合にはAIは学習に失敗します。2チャネルとは、画像の場合は1ピクセルにRGBの3原色の情報がありそのことを3チャネルと呼んだりしますが、ここでは五目並べの勝利判定なので2人のプレイヤの駒をそれぞれ表す2つのチャネルという意味です。そして学習に失敗する理由は、2チャネルを混ぜて1つの特徴マップを作成するからです。五目並べでいうと、2人のプレイヤの両方の駒を考慮して勝利判定することになります。しかし五目並べの勝利判定は相手の駒を数える必要はなく、自分の駒だけを見て求めることができます。よって相手の駒も計算に含めてしまうと処理が複雑になり、本来は勝っていると判定できない盤面でもたまたま計算結果が勝っていると判定してしまうことが起きると考えられます。
例えば ↑ のようにフィルターが抜き出した部分に相手のオレンジの駒が2つあるとして、それを含めた青駒の勝利判定計算結果が「青の勝利」と判定するとします。そしてこの盤面は他の箇所で青駒が勝利しているところがあるので、AIは計算が成功したと勘違いします。よって、↑ のような駒配置がたまたま他のデータにも含まれていてかつその盤面で青駒が実際に勝利している場合、AIはどんどん混乱していきます。
一方、盤面のプレイヤごとに分ける3次元データでは ↑ のようになります。これでももちろん、たまたま勝利判定の計算結果が実際には勝利条件を満たしていないのに「勝っている」と判定することもあり得ます。ただ相手の駒を計算に含めないので、そのリスクは軽減されると考えられます。
14.6. 補足、トレーニングデータとモデルについて
これらの学習に失敗するケースは、ある意味ではトレーニングデータが完璧ではないということを意味しています。盤面で表せるすべてのケースを持っているトレーニングデータならば、これらの問題が回避できるとも考えられます。しかしそのようなデータは膨大で現実的ではないので実現することは不可能です。
ここで示した学習に失敗するケースは、人の五目並べの勝利判定に対する知識を使って回避しています。言い換えるとトレーニングデータの不完全性を知識で補完しているとも見れます。さらに言い換えると、トレーニングデータがもう少し複雑でいろいろなパターンを保持していればモデルは少し適当でも良いといえます。
このようにデータが良ければモデルは少し適当でよい、また逆にデータが完全ではないならモデルには事前知識を入れる必要があるといえると思います。
参考
tensorflow公式API
tf.keras.layers.Conv2D
tf.keras.layers.Conv3D
tf.keras.layers.GlobalMaxPool2D
tf.keras.layers.GlobalMaxPool3D
tf.keras.layers.Permute
tf.keras.layers.Dense
web記事
畳み込みニューラルネットワークの基礎(3チャネルになるRGB画像を扱う場合の例が分かりやすい)

















